通信原理板块——信源信宿信息熵、离散信道信息传输速率和信道容量计算

微信公众号上线，搜索公众号小灰灰的FPGA,关注可获取相关源码，定期更新有关FPGA的项目以及开源项目源码，包括但不限于各类检测芯片驱动、低速接口驱动、高速接口驱动、数据信号处理、图像处理以及AXI总线等

对离散信道信息传输速率和离散信道容量计算
信源信息熵

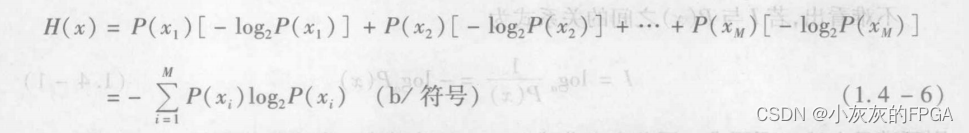
离散信道信息传输速率

互信息量I(x;y)
=H(x)-H(x/y)=H(y)-H(y/x)

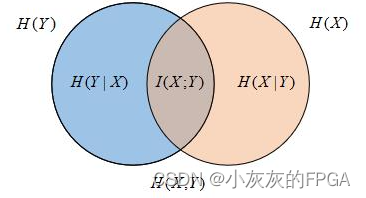
离散信道的信道容量

(1)例题一
某四元对称信道每个符号正确传输的概率为125/128,错成其它符号的概率为1/128。已知信源由“0”、“1”、“2”和“3”组成，且统计独立。如果消息传输速率为每秒1000个符号，四种取值的概率依次为1/4,1/4,3/8,1/8,。求：
①信源的信息熵；
②当前信源下，信道信息传输速率；
③信道容量。
解析：
①信源的信息熵H(x)
=1/4×[-log2(1/4)]+1/4×[-log2(1/4)]+
3/8×[-log2(3/8)]+1/8×[-log2(1/8)]+
=1.9056(b/符号)
②设x为1,2,3,4通道，对应y为1,2,3,4通道
信道的转移概率：P(y=j/x=i)
当i＝j时，P(y=j/x=i)=125/128，i,j=1,2,3,4
当i≠j时，P(y=j/x=i)=1/128，i,j=1,2,3,4
信宿的各个通道概率：
概率为1/4的y通道概率P(y=1)=P(y=2)
=1/4×125/128+1/4×1/128+3/8×1/128+1/8×1/128
=1/4
概率为3/8的y通道概率P(y=3)
=2×1/4×1/128+3/8×125/128+1/8×1/128
=95/256
概率为1/8的y通道概率P(y=4)
=2×1/4×1/128+3/8×1/128+1/8×125/128
=33/256
信宿的熵：
H(y)=2×1/4×[-log2(1/4)]
+95/256×[-log2(95/256)]
+33/256×[-log2(33/256)]
=1.9117(b/符号)

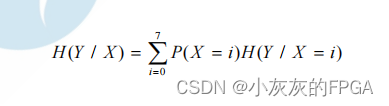
H(y/x=i)=H(125/128,1/128,1/128,1/128)
条件熵：
H(y/x)=(2×1/4+3/8+1/8)
×{((125/128)×[-log2(125/128)])
+3×((1/128)×[-log2(1/128)])}
=0.1975(b/符号)
互信息量：
I(x;y)=H(y)-H(y/x)
=1.9117(b/符号)-0.1975(b/符号)
=1.7142(b/符号)
信道信息传输速率：
R=r×I(x;y)
=1000(符号/s)×1.7142(b/符号)
=1714.2(b/符号)
③信道容量Ct，相对于最大互信息量
当互信息量I(x;y)最大时，此时I (x;y)max为信道容量C
当信源等概率分布时，达到信道容量
信源的各个取值概率
P(x=i)=1/4;i=1,2,3,4
信宿的各个通道概率：
P(y=i)=1/4×125/128+3×1/4×1/128=1/4
信宿的熵：
H(y)=4×1/4×[-log2(1/4)]
=2(b/符号)
H(y/x=i)=H(125/128,1/128,1/128,1/128)
条件熵：
H(y/x)=(4×1/4)
×{((125/128)×[-log2(125/128)])
+3×((1/128)×[-log2(1/128)])}
=0.1975(b/符号)
互信息量：
I (x;y)max=H(y)-H(y/x)
=2(b/符号)-0.1975(b/符号)
=1.8025(b/符号)
(2)例题二
某八进制对称信道，传输正确的概率为0.93，错成其他符号的概率平均为0.01。信源的概率分布为：4个符号为1/8；2个符号为1/16；2个符号为3/16。
求：
①信源信息熵；
②信道信息传输速率；
③信道容量。
解析：
①信源的信息熵H(x)
=4×1/8×[-log2(1/8)]+
2×1/16×[-log2(1/16)]+
2×3/16×[-log2(3/16)]
=2.9056(b/符号)
②设x为1,2,……,8通道，对应y为1,2,……,8通道
信道转移概率P(y=j/x=i),其中j,i=1,2,……,8
当i＝j时，P(y=j/x=i)=0.93
当i≠j时，P(y=j/x=i)=0.01
信宿的各个取值概率
概率为1/8的4个符号的y概率P(y=1)=P(y=2)=P(y=3)=P(y=4)=
1/8×0.93+3×1/8×0.01+2×1/16×0.01+2×3/16×0.01=0.125
概率为1/16的2个符号的y概率P(y=5)=P(y=6)=
4×1/8×0.01+1/16×0.93+1/16×0.01+2×3/16×0.01=0.0675
概率为3/16的2个符号的y概率P(y=7)=P(y=8)=
4×1/8×0.01+2×1/16×0.01+3/16×0.93+3/16×0.01=0.1825
信宿的熵为：H(y)=
=4×0.125×[-log2(0.125)]+
2×0.0675×[-log2(0.0675)]+
2×0.1825×[-log2(0.1825)]
=2.9056(b/符号)
条件熵H(y/x)

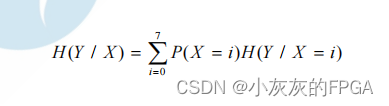
H(y/x=i)=H(0.93,0.01,0.01,0.01,0.01,0.01,0.01,0.01)
H(y/x)=
(4×1/8+2×1/16+2×3/16)×
(0.93×[-log2(-0.93)]+7×0.01×[-log2(-0.01)])
=0.5624(b/符号)
互信息量I(x;y)=H(y)-H(y/x)
=2.9056(b/符号)-0.5624(b/符号)
=2.343(b/符号)
信道信息传输速率：r=1符号/s
R=r×I(x;y)
=1×2.343(b/符号)
=2.343(b/s)
③信道容量Ct，相对于最大信息传输速率
当互信息量I(x;y)最大时，此时Rmax为信道容量C
当信源等概率分布时，达到信道容量
信源的各个取值概率
P(x=i)=1/8;i=1,2,……,8
信宿的各个取值概率
P(y=j)=1/8×0.93+7×1/8×0.01=1/8;j=1,2,……,8
信宿的熵H(Y)=8×1/8×[-log2(1/8)]=3(b/符号)
H(y/x=i)=H(0.93,0.01,0.01,0.01,0.01,0.01,0.01,0.01)
条件熵H(y/x)=
(8×1/8)×
(0.93×[-log2(-0.93)]+7×0.01×[-log2(-0.01)])
=0.5624(b/符号)
信道容量C=3(b/符号)- 0.5624(b/符号)=2.4376(b/符号)