浅聊反射系数——为何有共轭？

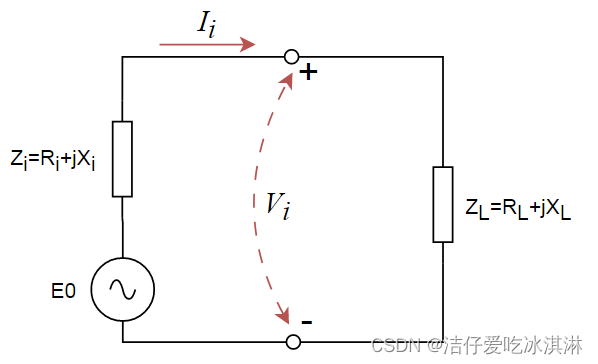
不知道大家是否有和我一样，有下列疑惑：为什么反射系数定义中分子有的时候存在共轭，有的时候又没有共轭。比如：

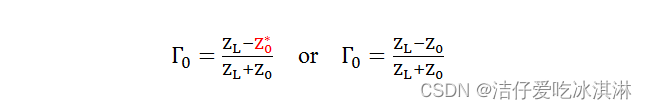
通俗解释就是：一般来说，Z ₀代表传输线的特性阻抗——为实数。所以多数时候，定义为右边的表达式；当Z ₀为复数时，就必须采用左边的定义式了。

不深究的话，一般来说到这里，回答也就结束了。

那么我就想问一问了，为什么Z₀为复数时，分子就必须有共轭呢？

按照我一般的写作习惯，为了更清楚、无歧义的阐述问题，会以公式为主体阐述文章。但今天这篇文章，我尽量避免这么做。

回想以传输线理论为基础推导过程，没有一处是因为将Z₀复数化后可以将分子改为共轭。所以分子的共轭是怎么来的呢？

直到我看到了一篇1960年代的论文“Power Waves and the Scattering Matrix”，我才明白了。大家有兴趣的话，可以自行下载。

先把灵魂点总结如下：

1、无反射匹配是以传输线理论为基础的行波理论，也叫恒等匹配或者Z₀匹配；
2、功率波理论以最大功率传输为基础，由Penfield最先提出。

1、基于行波理论的行波反射系数

基于行波理论分析一定存在着某种不便，才需另寻它法。不便在何处呢？

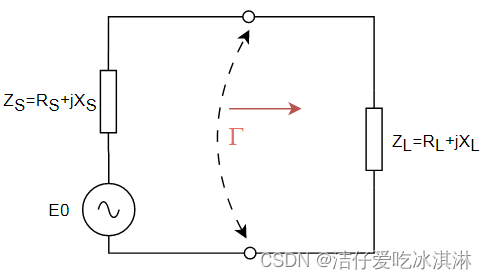
为了实现最大功率传输，则有：Z_S=Z_L*
带入行波理论定义的反射系数：

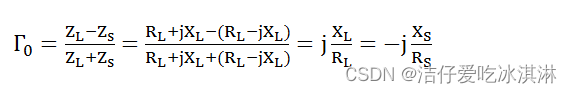
意味：共轭匹配时，反射系数的值由虚部与实部的比值决定，比值越大反射系数越大。此时基于行波理论定义的反射系数不在能反映功率的传输情况了。

为了方便后续的比较，此处定义入射波与反射波（Z₀为复数）：

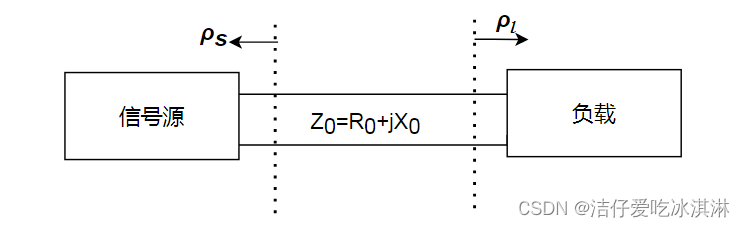
2、共轭匹配与功率波反射系数

功率波定义：

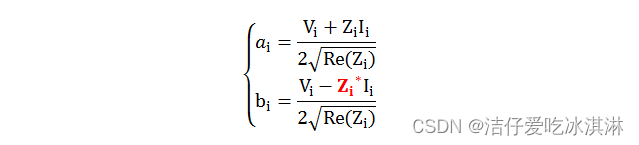
定义反射系数：

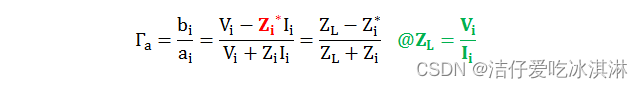
爱思考的读者可能会问：为什么 a_i 要这么定义呢？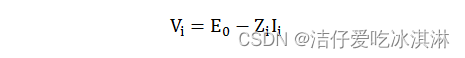

带入上述 a_i 的表达式得：

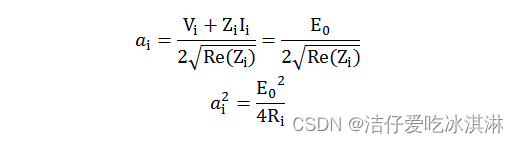
熟不熟悉？！！！
这不就是信号源的资用功率嘛！所以! 功率波的入射波是基于资用功率为基本参量定义的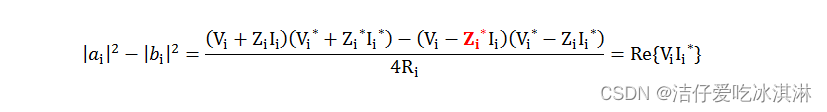

两者模平方的差值为：负载的消耗的实功率。

看到这里，我相信大家已经发现了：虽然我们基本不提及功率波，但实际上使用的、讨论的均为功率波，包括矢网测试、ADS、 HFSS仿真等S参数均为功率波的S参数。

但是呢，在射频领域经常把一些概念混为一谈，因为很多参数表征的是同一特性，平时工作时工程师们也经常不加区分，比如：反射系数、回波损耗、驻波比。这三者基本上表征的均为端口的匹配情况。

上面说了，以功率波定义的S参数的驻波比为：

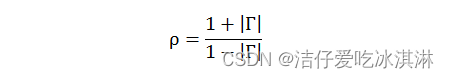
当Г=0时，ρ=1，仿佛此时为行波传输，无驻波。

但此时真的无驻波吗？

粉丝们可以看看之前写的一篇文章四臂螺旋天线的移相功分网络理论分析（一），里面提到了λ/4传输线做阻抗匹配的例子。

但凡端口阻抗存在虚部，必定要使负载阻抗与之成共轭关系，才能实现功率的最大传输，此时必定存在驻波！必定存在反射

3、总结

何时用行波理论？？何时用功率波理论呢？？

1》如果在意瞬时的波形变化，比如高速数字电路，以行波理论进行分析，要求阻抗连续，无反射，不求最大功率传输；
2》如果在意功率的最大传输，以功率波为基础进行分析，要求共轭匹配。

更进一步的，功率波只是Penfield提出的一种定义方法，一种数学表示，一种电流和电压之间的线性变换关系，但这种方法确能更清楚的理解射频系统电压与电流的功率关系。

之前的文章也提过，传输线理论也是一种麦克斯韦方程简化的电路表现形式。目的就是为了方便工程师们分析。功率波的提出也是如此。

欢迎点赞、转发、评论区讨论~~