PostgreSQL 技术内幕(十一)位图扫描

扫描算子在上层计算和底层存储之间，向下扫描底层存储的数据，向上作为计算的输入源，在SQL的执行层中，起着关键的作用。顺序、索引、位图等不同类型的扫描算子适配不同的数据分布场景。然而，扫描算子背后的实现原理是怎样的？如何评估不同扫描方法的代价和选择呢？

在往期的PG内幕直播讲解中，我们曾为大家介绍过PostgreSQL中的索引扫描。本次的直播，我们和大家分享了PostgreSQL中位图扫描的实现方式，讲解了位图扫描的源码实现，并从代价估算的角度对比了不同扫描方式。以下内容根据直播文字整理。

扫描方法分类及代价估算

在PostgreSQL的查询优化过程中，优化器会根据不同等价算子，构建许多符合条件的查询路径，并从中选择出代价最小的路径，转化为一个计划，传递给执行器执行。而评价路径优劣的依据是基于算子和系统统计信息估计出的不同路径的代价（Cost）。

常见的扫描方式有以下三种：

• 顺序扫描

当对无索引的字段进行查询，或者判断到查询将返回大量数据时，查询优化器将会使用顺序扫描方法，把表中所有数据块从前到后全部读一遍，然后找到符合条件的数据块。顺序扫描适合数据选择率高、命中大量数据的场景。

• 索引扫描

索引扫描先利用字段的索引数据，定位到数据的位置，然后再去数据表中读取数据。它适合选择率低、命中相对少数据的场景。

• 位图扫描

尽管索引数据一般比较少，但是它需要随机IO操作，相比顺序扫描所采用的顺序IO而言成本要更高，所以索引扫描的代价并不总是低。那如何在二者之间做平衡呢？对于选择率不高不低，命中率适中的场景，通常会使用到位图扫描。

位图扫描原理是将索引扫描中的随机IO，尽量转换成顺序IO，降低执行计划的代价。它首先访问索引数据，过滤出符合提交的数据的索引信息(CTID)，然后根据CTID来进行聚合和排序，将要访问数据页面有序化，同时数据访问的随机IO也转换成顺序IO。

接下来我们从代价估算的角度来看一下不同扫描方法的差异：

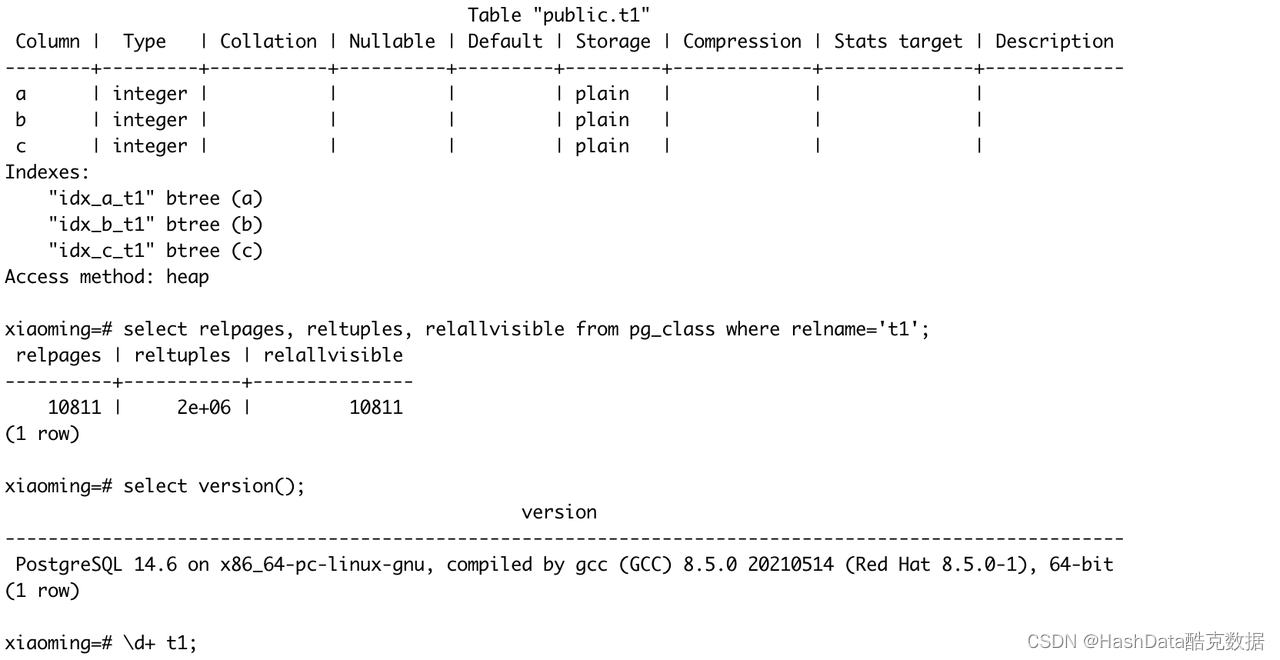图1：代价估算示例表

如图1所示，示例表中包含a、 b 、c三个字段；

索引信息：a、 b 、c 三个字段分别有一个btree索引；

统计信息：表内包含200w行数据，10811个数据页，全部可见。

代价估算示例

最简单的扫描 (select * from t1；)

xiaoming=# explain select * from t1;
                         QUERY PLAN
-------------------------------------------------------------
 Seq Scan on t1  (cost=0.00..30811.00 rows=2000000 width=12)
(1 row)

这是一个最简单的顺序扫描的示例，它的处理逻辑是：从表的segment文件中，按照顺序读取page页面到内存中，然后在内存中经过简单的CPU处理(MVCC判断)，返回适合的heap tuple数据。

从过程分析来看，执行代价可以归为两部分：IO_cost 和 CPU_cost。对于这个示例，它的IO pattern 是顺序扫描，IO_cost = 顺序扫描一个页面的代价(seq_page_cost) * 顺序扫描多少页面(relpages)；它对于tuple的处理，只是简单地判断MVCC，所以它的CPU_cost=处理一个tuple的代价(cpu_tuple_cost) * 多少个tuple(reltuples)。

我们使用下列SQL来计算这个计划的IO_cost 和 CPU_cost：

xiaoming=# SELECT relpages, current_setting('seq_page_cost') AS seq_page_cost,
  relpages * current_setting('seq_page_cost')::real AS io_cost
FROM pg_class WHERE relname='t1';
 relpages | seq_page_cost | io_cost
----------+---------------+---------
    10811 | 1             |   10811
(1 row)
cpu_cost = cpu_tuple_cost * reltuples
xiaoming=# select reltuples, current_setting('cpu_tuple_cost') as cpu_tuple_cost,
reltuples * current_setting('cpu_tuple_cost')::real AS cpu_cost
from pg_class where relname='t1';
 reltuples | cpu_tuple_cost | cpu_cost
-----------+----------------+----------
     2e+06 | 0.01           |    20000
(1 row)

total_cost = io_cost + cpu_cost = 30811, 刚好等于explain语句输出的cost(cost=0.00..30811.00 rows=2000000 width=12)。

不同扫描算子的代价对比

接下来我们通过同一个SQL select * from t1 where a <= 10000; 的不同执行计划的代价，来理解扫描算子的过程。

• 顺序扫描

xiaoming=# explain select * from t1 where a <= 10000;
                        QUERY PLAN
-----------------------------------------------------------
 Seq Scan on t1  (cost=0.00..35811.00 rows=20557 width=12)
   Filter: (a <= 10000)
(2 rows)

从Plan的输出可以看到，顺序扫描比我们代价估算示例中的Plan，多了一个Filter的阶段，整个Plan的cost增加到了35811。因为是顺序扫描，读取的数据是不变的，IO_cost是固定等于10811，所以增加的是CPU_cost。

从计算顺序扫描代价的函数代码中看，每一个tuple的代价cpu_per_tuple = cpu_tuple_cost + qpqual_cost.per_tuple， 其中qpqual_cost.per_tuple 和表达式的复杂度有关。在之前的示例中，因为没有表达式，所以qpqual_cost.per_tuple = 0。在当前这个代表式 where a <= 10000下，我们可以反推出 qpqual_cost.per_tuple= 0.0025。

disk_run_cost = spc_seq_page_cost * baserel->pages;
/* CPU costs */
get_restriction_qual_cost(root, baserel, param_info, &qpqual_cost);
startup_cost += qpqual_cost.startup;
cpu_per_tuple = cpu_tuple_cost + qpqual_cost.per_tuple;
cpu_run_cost = cpu_per_tuple * baserel->tuples;
/* tlist eval costs are paid per output row, not per tuple scanned */
startup_cost += path->pathtarget->cost.startup;
cpu_run_cost += path->pathtarget->cost.per_tuple * path->rows;
... 
... 
total_cost = startup_cost + cpu_run_cost + disk_run_cost;

• 索引扫描

xiaoming=# explain select * from t1 where a <= 10000;
                                 QUERY PLAN
----------------------------------------------------------------------------
 Index Scan using idx_a_t1 on t1  (cost=0.43..32243.95 rows=20557 width=12)
   Index Cond: (a <= 10000)
(2 rows)

索引扫描分为两个阶段：扫描索引数据， 根据索引数据扫描heap表数据，所以它的cost也可以分为两个阶段计算：

• 扫描索引数据的cost

对于 Btree索引来说，cost等于获取所需btree page的代价，btree pages的数量估算=relpages * 选择率。并且这些页面在磁盘上并不是按顺序存储的，因此索引数据的扫描模式是随机的。成本估算还包括处理每个index tuple的成本 cpu_index_tuple_cost，以及每行的过滤成本 cpu_operator_cost。

所以扫描索引数据的index_cost = relpages * selectivity rate * random_page_cost + reltuples * selectivity rate * (cpu_index_tuple_cost + cpu_operator_cost)。其中：

• relpages 是索引表的页面数
• reltuples 是索引表的tuple数
• selectivity rate = 20557 / reltuples

下面的SQL是计算索引数据的cost逻辑：

SELECT round(
  current_setting('random_page_cost')::real * pages +
  current_setting('cpu_index_tuple_cost')::real * tuples +
  current_setting('cpu_operator_cost')::real * tuples
) as bitmap_index_scan
FROM (
  SELECT relpages * 0.01027850 AS pages, reltuples * 0.01027850 AS tuples
  FROM pg_class WHERE relname = 'idx_a_t1'
) c;
 bitmap_index_scan
-------------------
               358
(1 row)

• 扫描数据的cost

对于heap data来说，我们能想到对于heap data的扫描，最坏的情况是每次ctid对应的heap tuple都是随机访问：io_cost_max = reltuples * selectivity rate * random_page_cost; 最好的情况ctid指向的heap tuple在磁盘上是有序的: io_cost_min = relpages * selectivity rate * seq_page_cost。

扫描heap data的io cost在[io_cost_min, io_cost_max]区间内，优化器是如何估算的呢？下面是cost_index函数里的代码：

// io_cost
csquared = indexCorrelation * indexCorrelation;
run_cost += max_IO_cost + csquared * (min_IO_cost - max_IO_cost);
// cpu_cost
cpu_per_tuple = cpu_tuple_cost + qpqual_cost.per_tuple;
cpu_run_cost += cpu_per_tuple * tuples_fetched;

其中核心是indexCorrelation这个字段，它的取值范围是 [-1,1]。当 indexCorrelation 的值接近 1 时，表示索引的顺序与表数据的顺序高度相关，即索引的排序与表数据的排序非常相似。当 indexCorrelation 的值接近 -1 时，表示索引的顺序与表数据的顺序高度负相关，即索引的排序与表数据的排序完全相反。当 indexCorrelation 的值接近 0 时，表示索引的顺序与表数据的顺序没有明显的相关性。

对于索引扫描，cache也会影响索引代价估算。思考一种情况，如果cache足够大，所有的页面只需要访问一次，因为后续所有对于这个页面的访问，都是访问数据库缓存。

• 位图扫描

xiaoming=# explain select * from t1 where a <= 10000;
                                                        QUERY PLAN
--------------------------------------------------------------------------------------------------
 Bitmap Heap Scan on t1  (cost=363.74..11559.98 rows=20557 width=12) (actual time=0.988..4.097 rows=20000 loops=1)
   Recheck Cond: (a <= 10000)
   Heap Blocks: exact=110
   ->  Bitmap Index Scan on idx_a_t1  (cost=0.00..358.61 rows=20557 width=0) (actual time=0.954..0.955 rows=20000 loops=1)
         Index Cond: (a <= 10000)
 Planning Time: 0.100 ms
 Execution Time: 4.971 ms

从Plan来看，Bitmap Scan也分为两个阶段：Bitmap Index Scan和Bitmap Heap Scan。

通过对比三种扫描算子的Plan输出可以发现，当前SQL，使用位图扫描的代价是最低的：

Bitmap scan cost(11559.98) < index scan cost(32243.95) < seq scan cost(35811)

位图扫描源码解析

位图扫描分为Bitmap Index Scan和Bitmap Heap Scan 两个阶段。

Bitmap Index Scan：扫描btree index的数据，构建并返回TID Bitmap；

Bitmap Heap Scan：依赖下层算子返回的TID Bitmap，扫描heap data，返回符合条件的tuple数据。

Bitmap Index Scan

Scan算子都有相同的三个阶段Init/Exec/End：

• 在Init阶段初始化扫描需要的数据结构，将查询条件转换成ScanKey；
• 在Exec阶段执行真正的扫描动作；
• 在End阶段清理相关的资源。

Bitmap Index Scan也不例外，ExecInitBitmapIndexScan函数实现了Bitmap Index Scan的Init逻辑，特定于Bitmap Index Scan扫描的数据结构struct BMScanOpaqueData，主要是记录扫描过程中tid bitmap访问位置信息。

typedef struct BMScanOpaqueData
{
    // 记录当前扫描的位置
    BMScanPosition      bm_currPos;
    bool                cur_pos_valid;
    /* XXX: should we pull out mark pos? */
    BMScanPosition      bm_markPos;
    // bmmarkpos() -- save the current scan position. 
    bool                mark_pos_valid;
} BMScanOpaqueData;

MultiExecBitmapIndexScan函数实现了Exec逻辑，主要通过调用index_getbitmap(scandesc, &bitmap)函数，获取bitmap，然后返回bitmap给上一级算子。因为示例表的索引都是btree索引，index_getbitmap指向的是btgetbitmap索引扫描函数。

btgetbitmap函数逻辑很简单：首先调用_bt_first/_bt_next逐条获取item；接着通过tbm_add_tuples添加到TIDBitmap里；最终构建一个完整的bitmap，核心就三个函数_bt_first/_bt_next/tbm_add_tuples。

_bt_first函数是索引扫描的起始，首先会调用_bt_preprocess_keys预处理扫描键，若扫描键条件无法满足，则设置BTScanOpaque->qual_ok为false并提前结束扫描。若没找到有用的边界keys，则需要调用_bt_endpoint从第一页开始，否则调用_bt_search从BTree的root节点_bt_getroot开始扫描，直至找到符合扫描键和快照的第一个叶子节点，之后调用二分查找_bt_binsrch找到符合扫描键的页内item偏移，最后将找到的页面载入到buffer中并返回tuple。

_bt_next函数会从当前页中尝试获取下一条tuple，若当前页已没有tuple，则调用_bt_steppage，_bt_steppage会拿到下一页块号，之后调用_bt_readnextpage读取该文件块中的内容，之后_bt_next尝试从中获取下一条tuple。重复上述过程，直至扫描结束。

tbm_add_tuples函数添加CTID，构建TIDBitmap数据结构，细节稍后讲解。

ExecEndBitmapIndexScan函数则用来清理相应的资源。

数据结构TIDBitmap

从上面的代码我们可以看到，btgetbitmap会一次返回符合条件的所有tid组成的TIDBitmap，而且TIDBitmap指向的内存区域大小是有限制的，等于work_mem * 1024 Byte. work_mem，默认值等于Heap Page Size。这些限制的存在使得TIDBitmap在设计上也有一些trade off。

typedef enum
{
    TBM_EMPTY,                  /* no hashtable, nentries == 0 */
    TBM_ONE_PAGE,               /* entry1 contains the single entry */
    TBM_HASH                    /* pagetable is valid, entry1 is not */
} TBMStatus;
typedef struct PagetableEntry
{
    BlockNumber blockno;        /* page number (hashtable key) */
    char        status;         /* hash entry status */
    bool        ischunk;        /* T = lossy storage, F = exact */
    bool        recheck;        /* should the tuples be rechecked? */
    tbm_bitmapword  words[Max(WORDS_PER_PAGE, WORDS_PER_CHUNK)];
} PagetableEntry;
struct TIDBitmap
{
    NodeTag     type;           /* to make it a valid Node */
    MemoryContext mcxt;         /* memory context containing me */
    TBMStatus   status;         /* see codes above */
    struct pagetable_hash *pagetable;   /* hash table of PagetableEntry's */
    int         nentries;       /* number of entries in pagetable */
    int         nentries_hwm;   /* high-water mark for number of entries */
    int         maxentries;     /* limit on same to meet maxbytes */
    int         npages;         /* number of exact entries in pagetable */
    int         nchunks;        /* number of lossy entries in pagetable */
    TBMIteratingState iterating;    /* tbm_begin_iterate called? */
    uint32      lossify_start;  /* offset to start lossifying hashtable at */
    PagetableEntry entry1;      /* used when status == TBM_ONE_PAGE */
    /* these are valid when iterating is true: */
    PagetableEntry **spages;    /* sorted exact-page list, or NULL */
    PagetableEntry **schunks;   /* sorted lossy-chunk list, or NULL */
    dsa_pointer dsapagetable;   /* dsa_pointer to the element array */
    dsa_pointer dsapagetableold;    /* dsa_pointer to the old element array */
    dsa_pointer ptpages;        /* dsa_pointer to the page array */
    dsa_pointer ptchunks;       /* dsa_pointer to the chunk array */
    dsa_area   *dsa;            /* reference to per-query dsa area */
};

在这个数据结构中，有几个重点需要关注的字段：

1. TBMStatus status 字段

• TBM_EMPTY代表当前TIDBitmap是空
• TBM_ONE_PAGE 代表 TIDBitmap中只有一个page的bitmap信息
• TBM_HASH 代表TIDBitmap中，bitmap信息是存储在hash table里

为什么会有TBM_ONE_PAGE和TBM_HASH的区别？因为如果TIDBitmap只存储一个PageTableEntry时，不需要花费时间构建动态hash表，查找时也不需要通过hash查找，只需要返回entry1即可。

1. struct pagetable_hash pagetable

page table是一个hash table，按照page维度存储bitmap，hash table的key是BlockNumber类型。value是一个PagetableEntry结构。一般来说可以使用hash table中的一个PagetableEntry用来存储一个page中哪些tid是符合查询需求的，block no对应 page number, PagetableEntry中bitmap words的第n bit代表page中第n+1个tuple。这样当我们构建bitmap时，相同block no的tid会被聚合到同一个key对应PagetableEntry中，btgetbitmap扫描完成所有存在的TID，都按照page聚合，类似图1的做法。

我们在前面看到，TIDBitmap的容量使用是有限制的(tbm_create调用指定)，如果一个page对应一个PageTableEntry，在有大量page需要构建bitmap的时候，内存使用肯定会超出。所以TIDBitmap里有一个maxentries字段，代表TIDBitmap最多可以有多少个PageTableEntry结构来存储bitmap。

为了满足超出maxentries个 page的bitmap 标记需求，当tbm_add_tuples添加tuple id时，page数量超出maxentries， bitmap就会进入调用tbm_lossify函数来使部分PageTableEntry从exact page 变成lossy page状态。即这些PageTableEntry不再代表某个page的bitmap，而是代表一组page的状态。

PagetableEntry的数据结构，在exact page和 lossy page状态下具有不同的含义：

typedef struct PagetableEntry
{
    BlockNumber blockno;        /* page number (hashtable key) */
    char        status;         /* hash entry status */
    bool        ischunk;        /* T = lossy storage, F = exact */
    bool        recheck;        /* should the tuples be rechecked? */
    tbm_bitmapword  words[Max(WORDS_PER_PAGE, WORDS_PER_CHUNK)];
} PagetableEntry;

Exact page状态：PageTableEntry对应一个page的bitmap

• blockno 就是page number
• ischunk 等于false，代表是exact
• words 的第n bit代表page的offset = n+1的tuple
• Lossy page状态：PageTableEntry等于一组page的状态
• blockno 是一个chunk_pageno, 对应一组page。这一组page的page no范围就是

tbm_mark_page_lossy函数实现了PageTableEntry从exact page向lossy page的转换

• ischunk等于true，代表是lossy
• words的第n bit代表 page no = chunk_page_no + n 的这个page，是有符合查询条件的tuple的

npages和nchunks字段分别代表，hash table里有多少exact page和lossy page。

1. PagetableEntry **spages 和 PagetableEntry **schunks

这两个字段主要是在BitmapHeapScan阶段使用的，spages和schunks在初始化bitamp iterator时构建，主要过程就是遍历hash table，根据exact page和lossy page的状态，分别添加到spages和schunks里，然后按照block no对spages和schunks进行排序。后续在Bitmap Heap Scan阶段，就可以顺序访问了。

1. dsa_*相关变量，都是和并行化扫描有关的。

了解数据结构后，tbm_add_tuples要做的事情就很清晰了:

• 根据page no在hash table里找到相应的bucket，然后找到对应的PageTableEntry(不存在则会创建)。但是如果此时只有一个PageTableEntry(即TBM_ONE_PAGE状态)，则直接返回entry1变量，不需要通过hash查找。
• 拿到entry后，根据tid，解析出offset，然后按照offset -1 去设置bitmap words的比特位即可。
• 如果在步骤1中，创建一个新的PageTableEntry，发现npages的数量超出了tbm->maxentries的值，则会调用tbm_lossify()函数，将TIDBITMap中的部分PageTableEntry转换成lossy page，同时按照exact page的减少和lossy page的增加，相应的修改npages和nchunks的值。
• 如果在步骤2中，因为tbm_lossy后，部分PageTableEntry是lossy状态的，如果此时步骤2拿到的是一个lossy page，则按照page no = chunk_page_no + n 的转换规则，设置对应的n个比特位。
• 如果最后tbm的全部entry都变成lossy状态了，则会触发tbm的扩容操作。maxentries = nentries * 2。

Bitmap Add

BitmapAnd节点获取从BitmapIndexScan节点生成的位图，并输出一个对所有输入位图进行AND操作的位图。

xiaoming=# explain select * from t1 where a <= 10000 and b <= 10000;
                                    QUERY PLAN
--------------------------------------------------------------------
 Bitmap Heap Scan on t1  (cost=717.57..1469.55 rows=211 width=12)
   Recheck Cond: ((b <= 10000) AND (a <= 10000))
   ->  BitmapAnd  (cost=717.57..717.57 rows=211 width=0)
         ->  Bitmap Index Scan on idx_b_t1  (cost=0.00..358.61 rows=20557 width=0)
               Index Cond: (b <= 10000)
         ->  Bitmap Index Scan on idx_a_t1  (cost=0.00..358.61 rows=20557 width=0)
               Index Cond: (a <= 10000)

Bitmap Or

同样的，BitmapOr节点获取从BitmapIndexScan节点生成的位图，并输出一个对所有输入位图进行OR操作的位图。其中，第一个输入位图用于存储OR操作的结果，并返回给调用者。

Bitmap Heap Scan

Bitmap Heap Scan 采用Bitmap Index Scan生成的bitmap(或者经过 BitmapAnd 和 BitmapOr 节点通过一系列位图集操作后，生成的bitmap)来查找相关数据。位图的每个page可以是精确的（直接指向tuple的）或有损的（指向包含至少一行与查询匹配的page）。

xiaoming=# explain select * from t1 where a <= 10000;
                                                        QUERY PLAN
--------------------------------------------------------------------------------------------------
 Bitmap Heap Scan on t1  (cost=363.74..11559.98 rows=20557 width=12) (actual time=0.988..4.097 rows=20000 loops=1)
   Recheck Cond: (a <= 10000)
   Heap Blocks: exact=110
         -> ... Bitmap Index Scan || Bitmap And || Bitmap Or

Bitmap Heap Scan阶段的实现函数BitmapHeapNext：

static TupleTableSlot *BitmapHeapNext(BitmapHeapScanState *node) {
    //下级节点返回TIDBitmap结构
    tbm = (TIDBitmap *) MultiExecProcNode(outerPlanState(node));
    node->tbm = tbm;
    // 初始化扫描迭代器，构造tbm->spages和tbm->schunks用于扫描，
    // 并两个数组按照page id排序
    node->tbmiterator = tbmiterator = tbm_begin_iterate(tbm);
    node->tbmres = tbmres = tbm_iterate(tbmiterator);
 
 
    // 读取一个block，lossy page就是在这个case下处理的
    // 读取一整个heap page, 保存在scan的buffer中，用于下次扫描
    table_scan_bitmap_next_block(scan, tbmres)
 
 
    // 如果是lossy的，则会循环读取，直到找到一个满足Filter条件的tuple.
    // 如果是exact的，则直接根据tmbres中的当前entry指针，直接seek
    // 到next offset指向的tuple..
    table_scan_bitmap_next_tuple(scan, tbmres, slot)
 
 
    return slot;
}

代码核心逻辑如下：

1. 下层算子的执行函数MultiExecProcNode()返回了一个TIDBitmap；
2. 调用tbm_generic_begin_iterate()基于tbm构建了一个iterator；
3. 每次循环获取一个指向具体页面的TBMIterateResult结构，通过table_scan_bitmap_next_block一次读取一个page到ScanDesc的rs_buffer里；然后调用table_scan_bitmap_next_tuple，根据TBMIterateResult里的偏移，在内存buffer里获取相应的tuple；
4. 根据bitmap中PageTableEntry的状态(即exact还是lossy), 读取指定的page；如果是exact page，则直接读取指定offset的tuple；如果是lossy的，则根据filter过滤掉不必要的tuple，然后调用recheck检查其他查询条件；
5. 调用recheck函数，判断tuple是否满足查询条件，不满足则继续next；满足则返回tuple给上层节点。

代价分析

Bitmap Index Scan的代价估算就是Index Scan的访问索引数据的代价，即如下计算公式：

SELECT round(
  current_setting('random_page_cost')::real * pages +
  current_setting('cpu_index_tuple_cost')::real * tuples +
  current_setting('cpu_operator_cost')::real * tuples
) as bitmap_index_scan
FROM (
  SELECT relpages * 0.01027850 AS pages, reltuples * 0.01027850 AS tuples
  FROM pg_class WHERE relname = 'idx_a_t1'
) c;
 bitmap_index_scan
-------------------
               358
(1 row)

Bitmap Heap Scan的cost计算比较复杂，逻辑在cost_bitmap_heap_scan这个函数。首先是Bitmap Heap Scan读取page的数量的估算计算公式：

图2：page数量的估算公式

公式中的sel是选择率, 在我们这个例子里sel=0.01027850。其次单个页面的获取成本估计在 seq_page_cost 和 random_page_cost 之间，如果tid分布很松散，则趋近于random_page_cost; 如果tid分布聚集性好，则趋近于seq_page_cost。在同时存在exact和lossy bitmap时，对于exact bitmap, 处理tuple的数量等于sel * reltuples。对于lossy bitmap，则需要对lossy page上的每一个tuple进行recheck操作。在我们的例子中，不会超出TID Bitmap的 max_entries数量，所以我们所有的bitmap都是精确的。

下面这个SQL就是模拟Bitmap Scan的cost计算逻辑(entry全是exact page的情况)。计算的total_cost值11560，刚好和我们前面Plan给出来的值11559.98相近。

WITH t AS (
  SELECT relpages,
    least(
      (2 * relpages * reltuples * 0.01027850) /
      (2 * relpages + reltuples * 0.01027850), relpages
    ) AS pages_fetched,
    round(reltuples * 0.01027850) AS tuples_fetched,
    current_setting('random_page_cost')::real AS rnd_cost,
    current_setting('seq_page_cost')::real AS seq_cost
  FROM pg_class WHERE relname = 't1'
), s AS(
  select pages_fetched, rnd_cost - (rnd_cost - seq_cost) *
  sqrt(pages_fetched / relpages) AS cost_per_page, tuples_fetched 
  tuples_fetched from t
),
costs(startup_cost, run_cost) AS (
  SELECT
    ( SELECT round(
        358 /* child node cost */ +
        0.1 * current_setting('cpu_operator_cost')::real *
        reltuples * 0.01027850
      )
      FROM pg_class WHERE relname = 'idx_a_t1'
    ),
    ( SELECT round(
        cost_per_page * pages_fetched +
        current_setting('cpu_tuple_cost')::real * tuples_fetched +
        current_setting('cpu_operator_cost')::real * tuples_fetched
      )
      FROM s
    )
)
SELECT startup_cost, run_cost, startup_cost + run_cost AS total_cost
FROM costs;
 startup_cost | run_cost | total_cost
--------------+----------+------------
          363 |    11197 |      11560
(1 row)

位图扫描限制

目前大多数的分析场景，都是基于一个前提，存储的随机IO cost远远大于顺序 IO cost的基础上(在pg中是4倍的差距，默认random_page_cost=4, seq_page_cost=1)。但是今天大量新的存储硬件或者云原生存储的使用场景下，随机IO和顺序IO的差距已经不再是这种关系。当我们在启用bitmap scan的时候，一定要仔细考虑这其中的问题。例如下面的场景：

1. 新型Nvme SSD的随机IO能力已经非常强，顺序IO和随机IO的性能差异已经显著缩小，io的延迟也很低。
2. 在存算分离架构中，访问云存储的网络延迟、IO延迟比较大，优化器要考虑IO合并和prefetching对cost的影响。云存储的IO Pattern也很并发的从不同节点读写具备更高的性能。单次IO请求的延迟比较高。

总结

正常情况下，PostgreSQL 优化器可以选择出来一种最优的方式来执行，但不保证总是可以生成最优化的执行计划。

任何优化都是一个系统工程，而不是一个单点工程，通过不同资源的消耗比例来提升整体性能，Bitmap Scan也并非完美无瑕，其优化理念是通过Bitmap的生成过程中增加内存和CPU成本来降低IO成本。

对于高性能存储或者内存资源充足的情况而言，并不一定总是发生物理IO，那么IO就不会成为瓶颈，如果去做Bitmap的生成，反倒是一种浪费。此时可以根据具体的IO能力，考虑禁用Bitmap scan等方案，从而实现整体计划的最优化。