代码随想录训练营Day1:二分查找与移除元素

本专栏内容为：代码随想录训练营学习专栏，用于记录训练营的学习经验分享与总结。

文档讲解：代码随想录
视频讲解：二分查找与移除元素

💓博主csdn个人主页：小小unicorn
⏩专栏分类：C++
🚚代码仓库：小小unicorn的代码仓库🚚
🌹🌹🌹关注我带你学习编程知识

二分查找

题目分析

题目描述：给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

题目来源：704.二分查找

解题思路：

这道题目的前提是数组为有序数组，同时题目还强调数组中无重复元素，因为一旦有重复元素，使用二分查找法返回的元素下标可能不是唯一的，这些都是使用二分法的前提条件，当大家看到题目描述满足如上条件的时候，可要想一想是不是可以用二分法了。

二分查找涉及的很多的边界条件，逻辑比较简单，但就是写不好。例如到底是 while(left < right) 还是 while(left <= right)，到底是right = middle呢，还是要right = middle - 1呢？

大家写二分法经常写乱，主要是因为对区间的定义没有想清楚，区间的定义就是不变量。要在二分查找的过程中，保持不变量，就是在while寻找中每一次边界的处理都要坚持根据区间的定义来操作，这就是循环不变量规则。

写二分法，区间的定义一般为两种，左闭右闭即[left, right]，或者左闭右开即[left, right)。

写法一：

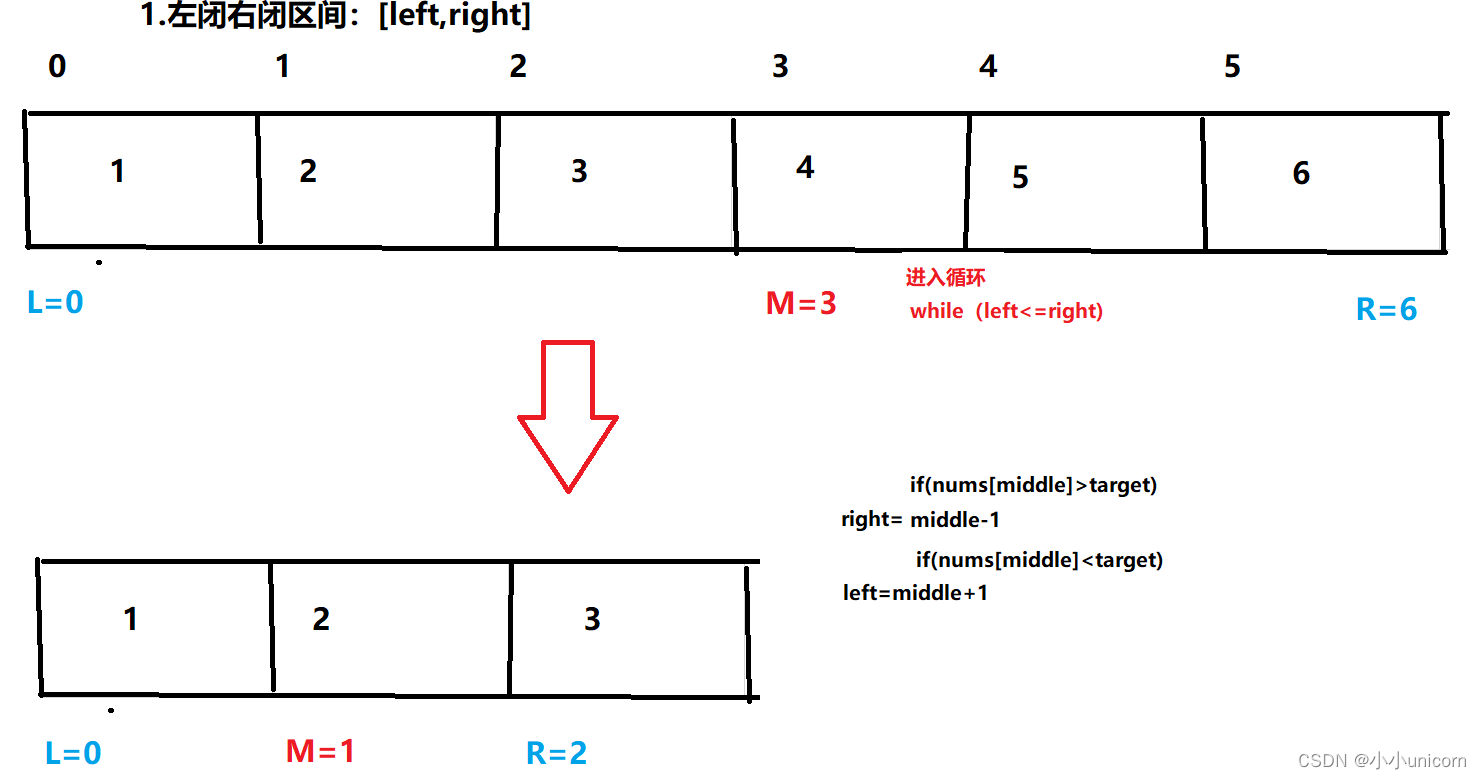
第一种写法，我们定义 target 是在一个在左闭右闭的区间里，也就是[left, right] 。

在这个区间内要有以下两点：

1.while (left <= right)
要使用 <= 。
这是因为left == right是有意义的，所以使用 <=。

2.if (nums[middle] > target)
那么 right 要赋值为 middle - 1。
这是因为当前这个nums[middle]一定不是target，那么接下来要查找的左区间结束下标位置就是 middle - 1
例如在数组：1,2,3,4,7,9,10中查找元素2，如图所示：

代码解决：

class Solution 
{
public:
    int search(vector<int>& nums, int target) 
    {
        //定义左闭右闭区间
           int left=0;
           int right=nums.size()-1;
        while(left<=right)
        {
            int middle=left+((right-left)/2);
            //说明target在左区间
            if(nums[middle]>target)
              right=middle-1;
            //target在右区间
            else if(nums[middle]<target)
              left=middle+1;
            else
            //找到了
              return middle;
        }
        //未找到目标值
        return -1;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

时间复杂度：O(log n)
空间复杂度：O(1)

写法二：

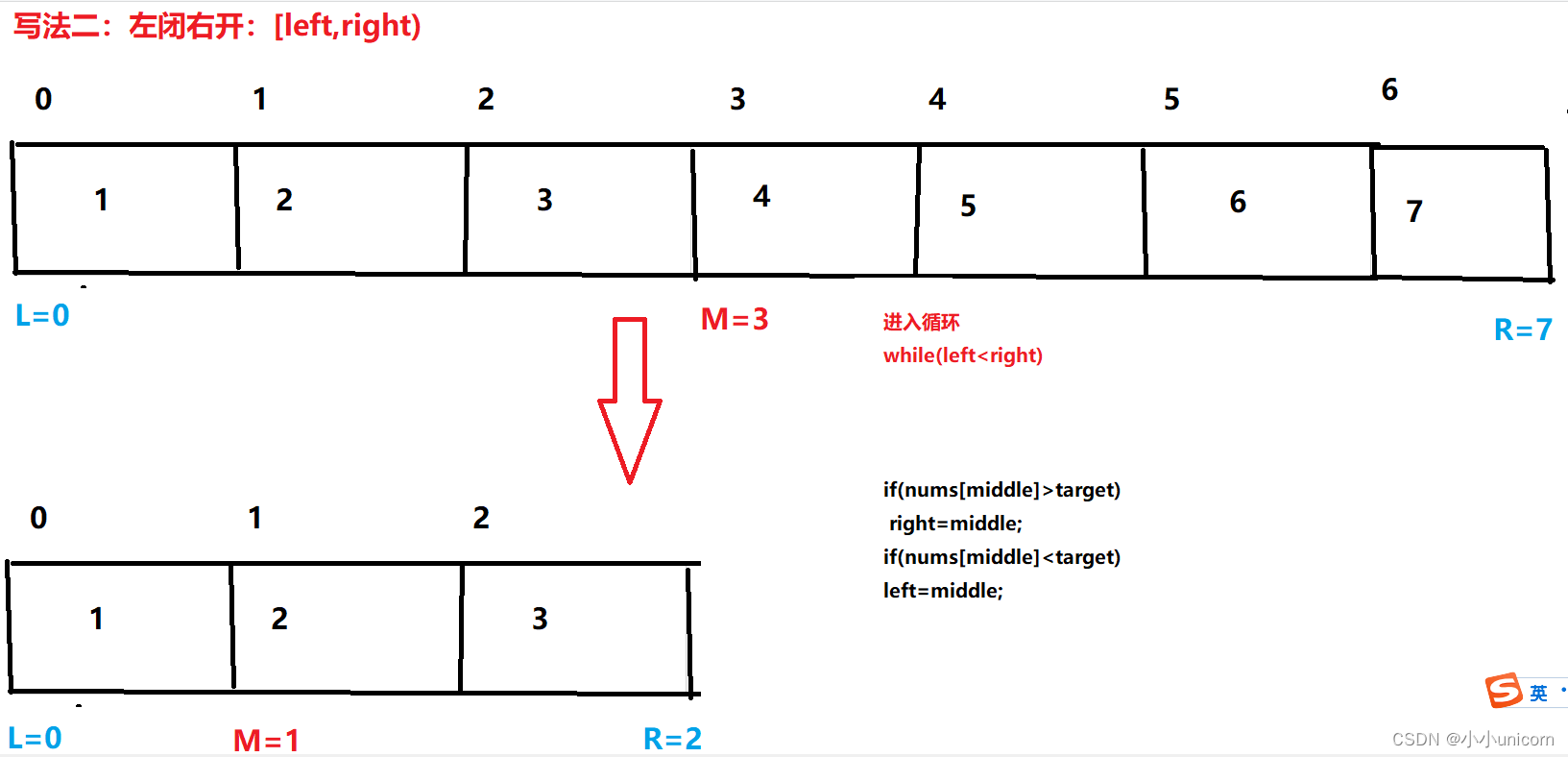
如果说定义 target 是在一个在左闭右开的区间里，也就是[left, right) ，那么二分法的边界处理方式则截然不同。

有如下两点：

1.while (left < right)
这里使用 <
这是因为left == right在区间[left, right)是没有意义的

2.if (nums[middle] > target)
right 更新为 middle
这是因为当前nums[middle]不等于target，去左区间继续寻找，而寻找区间是左闭右开区间，所以right更新为middle，即：下一个查询区间不会去比较nums[middle]
在数组：1,2,3,4,7,9,10中查找元素2，如图所示：（注意和方法一的区别）

代码解决：

class Solution {
public:
    int search(vector<int>& nums, int target) 
    {
        int left = 0;
        int right = nums.size(); // 定义target在左闭右开的区间里，即：[left, right)
        while (left < right) 
        { // 因为left == right的时候，在[left, right)是无效的空间，所以使用 <
            int middle = left + ((right - left) >> 1);
            if (nums[middle] > target) 
            {
                right = middle; // target 在左区间，在[left, middle)中
            } 
            else if (nums[middle] < target) 
            {
                left = middle + 1; // target 在右区间，在[middle + 1, right)中
            } 
            else 
            { // nums[middle] == target
                return middle; // 数组中找到目标值，直接返回下标
            }
        }
        // 未找到目标值
        return -1;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

移除元素

题目分析：

题目描述：给你一个数组 nums 和一个值 val，你需要 原地 移除所有数值等于 val 的元素，并返回移除后数组的新长度。
不要使用额外的数组空间，你必须仅使用 O(1) 额外空间并 原地 修改输入数组。
元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
题目来源：27.移除元素

思路：

暴力：

两层for循环，一个for循环遍历数组元素 ，第二个for循环更新数组。

// 时间复杂度：O(n^2)
// 空间复杂度：O(1)
class Solution {
public:
    int removeElement(vector<int>& nums, int val) {
        int size = nums.size();
        for (int i = 0; i < size; i++) {
            if (nums[i] == val) { // 发现需要移除的元素，就将数组集体向前移动一位
                for (int j = i + 1; j < size; j++) {
                    nums[j - 1] = nums[j];
                }
                i--; // 因为下标i以后的数值都向前移动了一位，所以i也向前移动一位
                size--; // 此时数组的大小-1
            }
        }
        return size;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

时间复杂度：O(n^2)
空间复杂度：O(1)

双指针法：

双指针法（快慢指针法）： 通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。
定义快慢指针

快指针：寻找新数组的元素 ，新数组就是不含有目标元素的数组
慢指针：指向更新 新数组下标的位置

代码解决

class Solution 
{
public:
    int removeElement(vector<int>& nums, int val) 
    {
       int slowIndex=0;
       for(int fastIndex=0;fastIndex<nums.size();fastIndex++)
       {
           //只要不等于val就往后移动
           if(val!=nums[fastIndex])
            nums[slowIndex++]=nums[fastIndex];
       }
       return slowIndex;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

时间复杂度：O(n)
空间复杂度：O(1)

总结：

在今天，我们通过两道典型例题，知道了什么是二分法，用到了双指针算法思想，希望通过这两道例题，能对双指针和二分法有更深层的理解。