• VEX —— Quaternion|Euler Angle

    目录

    一，四元数相关概念

    四元数

    欧拉角

    常用四元数相关函数

    相互转换

    二，案例

    案例：沿面中心翻转

    案例：路径导弹

    案例：RBD刚体还原过渡

    案例：拉直螺旋线

    案例：卷曲螺旋线

    一，四元数相关概念

    四元数

    • 在vex内四元数为（（x，y，z），w）；
    1. //VEX内获得四元数
    2. vector4 quaternion(matrix3 rotations) //仅应用矩阵的旋转信息
    3. ​vector4 quaternion(float angle, vector axis)
    4. vector4 quaternion(vector angleaxis) //方向为旋转轴，大小为旋转角度
    5.  
    6. vector4  eulertoquaternion(vector rotations, int order)

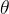    注，数学运算，如绕某向量 K=(K_{x}, K_{y}, K_{z}) 旋转\theta，则四元数为：

    • (x，y，z)  =  (K_{x}, K_{y}, K_{z}) *  \sin \frac{\theta }{2} 
    • w =  \cos \frac{\theta }{2} 
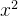    • 且满足条件：x^{2}+y^{2}+z^{2}+w^{2}=1

    欧拉角

    由环绕三个轴旋转的角度组成的矢量表示

    • 绕著x轴的旋转（Roll），绕著交点线的旋转（Pitch），绕著z轴的旋转（Yaw）；
    • 任何旋转矩阵都是由三个基本旋转矩阵复合而成的；
    • 不同旋转顺序，结果不同，默认旋转顺序XYZ；
    1. //VEX内获得欧拉角
    2. vector  quaterniontoeuler(vector4 orient, int order)

    注，可使用Transform节点应用欧拉角；

    常用四元数相关函数

    dihedral()

    quaternion()

    qrotate()

    qmultiply()

    qinvert()

    qdistance()

    qconvert()

    eulertoquaternion()

    quaterniontoeuler()

    slerp()

    相互转换

    1. //矩阵转四元数
    2. matrix m = detail(1, 'xform');
    3. vector4 q = quaternion(matrix3(m));
    1. //四元数转矩阵
    2. vector4 q = quaternion(ch('ang'), chv('axis'));
    3. matrix3 m = qconvert(q);
    1. //欧拉角转矩阵或四元数
    2. v@euler_angle = degrees(chv('ang'));
    3. vector4 q = eulertoquaternion(@euler_angle);
    4. matrix3 m = qconvert(q);
    1. //四元数或矩阵，获取欧拉角
    2. matrix m = detail(1, 'xform');
    3. vector4 q = quaternion(matrix3(m));
    4. v@euler_angle = degrees(quaterniontoeuler(q, 0));

    二，案例

    • 设置旋转，dihedral，quaternion，orient（可用于copy）；
    • 合并旋转，qmultiply
    • 应用旋转，qrotate

    参考：使用houdini绑定系统里的rigdoctor节点来提取矩阵_哔哩哔哩_bilibili

    案例：沿面中心翻转

    1. //point层级，并获取所属面的其他点
    2. int pts[] = primpoints(0, @primnum);
    3. vector pos0 = point(0, 'P', pts[0]);
    4. vector pos1 = point(0, 'P', pts[1]);
    5. vector pos2 = point(0, 'P', pts[2]);
    6. vector pos3 = point(0, 'P', pts[3]);
    1. //方法一，先归到中心点旋转，在还原
    2. vector center = (pos0+pos1+pos2+pos3)/4;
    3. vector axis = normalize(pos1-pos0);
    4.  
    5. @P -= center;
    6.  
    7. float ang = @Time;
    8. vector4 q = quaternion(ang, axis);
    9. @P = qrotate(q,@P);
    10.  
    11. @P += center;
    12.  
    1. //方法二，使用maketransform
    2. vector pivot = (pos0+pos1+pos2+pos3)/4;
    3. vector axis = normalize(pos1-pos0);
    4.  
    5. //直接绕axis旋转
    6. float ang = @Time;
    7. vector4 q_r = quaternion(ang, axis);
    8. vector r = degrees(quaterniontoeuler(q_r, 0));
    9.  
    10. @P *= maketransform(0,0,0,r,1,pivot,0);
    11.  
    12. //绕x轴旋转，中心点旋转偏移到axis
    13. float ang = @Time;
    14. vector dir = set(1,0,0);
    15. vector r = dir * degrees(ang);
    16. vector4 q_pr = dihedral(dir, axis);
    17. vector pr = degrees(quaterniontoeuler(q_pr, 0));
    18.  
    19. @P *= maketransform(0,0,0,r,1,pivot,pr);
    1. //方法三，使用函数instance
    2. vector pivot = (pos0+pos1+pos2+pos3)/4;
    3. vector axis = normalize(pos1-pos0);
    4.  
    5. float ang = @Time;
    6. vector4 orient = quaternion(ang, axis);
    7. @P *= instance(pivot,0,1,0,orient,pivot);
    1. //方法二，手搓矩阵(即将本身或局部坐标系恢复到世界坐标系，旋转后，在还原到原坐标系)
    2. vector center = (pos0+pos1+pos2+pos3)/4;
    3. vector xaxis = normalize(pos1-pos0);
    4. vector yaxis = normalize(prim(0,'N',@primnum));
    5. vector zaxis = normalize(cross(xaxis, yaxis));
    6.  
    7. matrix m = set(xaxis, yaxis, zaxis, center);
    8. m.xa = m.ya = m.za = 0;
    9. @P *= invert(m);
    10.  
    11. float ang = @Time;
    12. vector4 q = quaternion(ang, set(1,0,0));
    13. @P = qrotate(q, @P);
    14.  
    15. @P *= m;

    案例：路径导弹

    1. //方法一
    2. vector tangentu = -primuv(1, 'tangentu', 0, ch('u'));
    3. vector tangentv = primuv(1, 'tangentv', 0, ch('u'));
    4. vector pos = primuv(1, 'P', 0, ch('u'));
    5.  
    6. vector4 rot1 = dihedral(set(1,0,0), tangentu);
    7. vector4 rot2 = quaternion(@Time*10, set(1,0,0));
    8. vector4 rot = qmultiply(rot1, rot2);
    9.  
    10. //如不是pack物体
    11. @P = qrotate(rot, @P) + pos;
    12.  
    13. //如是pack物体，使用以下代码
    14. @P = pos;
    15. matrix3 m = qconvert(rot);
    16. setprimintrinsic(0, "transform", 0, m);
    1. //方法二
    2. vector x_axis = -primuv(1, 'tangentu', 0, ch('u'));
    3. vector y_axis = primuv(1, 'tangentv', 0, ch('u'));
    4. vector z_axis = cross(x_axis, y_axis);
    5. vector pos = primuv(1, 'P', 0, ch('u'));
    6.  
    7. matrix m = set(normalize(x_axis), normalize(y_axis), normalize(z_axis), pos);
    8. vector4 q = quaternion(@Time*10, set(1,0,0));
    9.  
    10. @P = qrotate(q, @P);
    11. @P *= m;

    案例：RBD刚体还原过渡

    • RBD刚体的中心和质心（rest信息）的区别；

    注，pack对象intrinsic属性

    • transform，存储旋转信息，使用setprimintrinsic函数设置；
    • packedfulltransform，存储所有的变换信息（只读）；
    1. //DOP内部还原的原始位置为rest，注意设置input端口
    2. //直接用rbdbulletsolver(SOP)，原始位置还是originP
    3. float bias = chramp('bias', fit(@Frame-@offset*10,75,125,0,1));
    4. matrix3 cm = primintrinsic(0, 'transform', @ptnum);
    5. matrix3 blend = slerp(cm, 3@m, pow(bias,2));
    6. setprimintrinsic(0, 'transform', @ptnum, blend);
    7. v@P = lerp(@P, v@rest, bias);
    1. float bias = chramp('bias', fit(@Frame-@offset*10,75,125,0,1));
    2. matrix fm = getpackedtransform(0, @ptnum);
    3. vector t = cracktransform(0, 0, 0, 0, 4@fm);
    4. translate(4@fm, -t);
    5. translate(4@fm, v@rest);
    6. matrix blend = slerp(fm, 4@fm, bias);
    7. setpackedtransform(0, @ptnum, blend);

    案例：拉直螺旋线

    • 原理1：以0号点为中心旋转1号点及后续所有点到Y轴上，在以1号点为中心旋转2号点及后续所有点到Y轴上，依次类推；可使用solver或循环（在旋转一次的基础在旋转，容易理解）；
    • 原理2，每层循环记录上次循环的上一个拉直点(prepos)；每层循环先移动到原点旋转Y轴，在加上prepos；
    • 原理3，先记录每个点与前一个点的旋转信息，每个点依次旋转到前点和前前点的方向上，最后对齐到Y轴；
    • for等循环体内的point()始终都是读取输入端口的属性，setpointattrib始终会在输出时设置；
    1. //solver节点内，detail层级
    2. int i = @Frame;
    3. vector pos0 = point(0, 'P', i-1);
    4. vector pos1 = point(0, 'P', i);
    5. vector4 rot = dihedral(pos1-pos0, set(0,1,0));
    6.  
    7. vector pos = qrotate(rot, pos1-pos0);
    8. setpointattrib(0, 'P', i, pos+pos0);
    9.     
    10. for(int j=i+1; j<npoints(0); j++){
    11.     vector pos2 = point(0, 'P', j);
    12.     pos2 = qrotate(rot, pos2-pos0);
    13.     setpointattrib(0, 'P', j, pos2+pos0);
    14. } 
    1. //point层级（也可是detail层级），每层循环互不关联
    2. vector prepos = 0;
    3.  
    4. for(int i=1; i< @Frame; i++){
    5.     vector pivot  = point(0, 'P', i-1);
    6.     vector pos = point(0, 'P', i);    
    7.     vector4 rot = dihedral(pos-pivot, set(0,1,0));    
    8.     
    9.     if(@ptnum>=i){
    10.         vector mpos = qrotate(rot, @P-pivot);
    11.         //@P=mpos+prepos; //会对下一循环影响
    12.         setpointattrib(0, 'P', @ptnum, mpos+prepos);
    13.      }
    14.     
    15.      prepos = qrotate(rot, pos-pivot)+prepos;
    16. }
    1. //detail层级
    2. vector pos[] = array();
    3. for(int i=0; i<@numpt; i++){
    4.     pos[i] = point(0, 'P', i);
    5. }
    6.  
    7. for(int i=1; i<@Frame; i++){
    8.     vector4 rot = dihedral(pos[i]-pos[i-1], set(0,1,0));      
    9.     for(int j=i; j<@numpt; j++){
    10.         pos[j] = qrotate(rot, pos[j]-pos[i-1]);
    11.         pos[j] += pos[i-1];
    12.     }
    13. }
    14.  
    15. for(int i=0; i<@numpt; i++){
    16.     setpointattrib(0, 'P', i, pos[i]);
    17. }
    18.  
    1. //point层级，当前点位置与前一个点位置的旋转信息
    2. vector pos1 = point(0, 'P', @ptnum-1);
    3. vector pos2 = point(0, 'P', @ptnum-2);
    4. vector4 rot = dihedral(@P-pos1, pos1-pos2);
    5. if(@ptnum==1)
    6.     rot = dihedral(@P, set(0,1,0));
    7. p@rot = rot;
    8.  
    9. vector4 rot1 = set(0,0,0,1);
    10. p@rot = slerp(rot1, p@rot, ch('val'));
    1. //point层级，每个点都是相当于先对齐前一个点，在对齐前前点...，直到最后对齐Y轴
    2. vector prepos = 0;
    3. vector4 prerot = set(0,0,0,1);
    4.  
    5. for(int i=0; i<=@ptnum; i++){
    6.     vector pos = point(0, 'P', i);
    7.     vector pivot = point(0, 'P', i-1);
    8.     prerot = qmultiply(prerot, point(0, 'rot', i));
    9.     pos -= pivot;
    10.     pos = qrotate(prerot, pos);
    11.     pos += prepos;
    12.     prepos = pos;
    13.     @P = pos;
    14. }

    案例：卷曲螺旋线

    • 原理1：每个点，以该点为中心，先将之前所有点旋转拉平，在旋转卷曲；
    • 原理2：先记录每个点与后一个点的旋转信息；
    1. //point层级，for循环在上一循环基础上循环，也可solver(SOP)
    2. int num = chi('num');
    3. if(@ptnum < num){
    4.     vector pivot = point(0, 'P', num);
    5.     vector prepos =  point(0, 'P', num-1);
    6.     vector nextpos =  point(0, 'P', num+1);
    7.     float ang = ch('ang')*pow(point(0, 'curveu', num)+0.01,-0.8);
    8.     
    9.     vector axis = normalize(cross(set(0,1,0), nextpos-pivot));
    10.     vector4 rot1 = quaternion(ang, axis);
    11.     vector4 rot2 = dihedral(prepos-pivot, pivot-nextpos);
    12.     vector4 rot = qmultiply(rot1, rot2);
    13.  
    14.     @P -= pivot;
    15.     @P = qrotate(rot, @P);
    16.     @P += pivot;
    17. }
    1. vector pos[] = array();
    2. for(int i=0; i<@numpt; i++){
    3.     pos[i] = point(0, 'P', i);
    4. }
    5.  
    6. for(int i=0; i<chi('num'); i++){
    7.     vector pivot = point(0, 'P', i);
    8.     vector prepos =  point(0, 'P', i-1);
    9.     vector nextpos =  point(0, 'P', i+1);
    10.     float ang = ch('ang')*pow(point(0, 'curveu', i)+0.01,-0.8);
    11.     
    12.     vector axis = normalize(cross(set(0,1,0), nextpos-pivot));
    13.     vector4 rot1 = quaternion(ang, axis);
    14.     vector4 rot2 = dihedral(prepos-pivot, pivot-nextpos);
    15.     vector4 rot = qmultiply(rot1, rot2);
    16.  
    17.     for(int j=0; j
    18.         pos[j] -= pivot;
    19.         pos[j] = qrotate(rot, pos[j]);
    20.         pos[j] += pivot;
    21.     }
    22. }
    23.  
    24. for(int i=0; i<chi('num'); i++){
    25.     setpointattrib(0, 'P', i, pos[i]);
    26. }
    1. //point层级，当前点位置与后一个点位置的旋转并卷曲信息
    2. vector pivot = point(0, 'P', @ptnum+1);
    3. vector pos2 = point(0, 'P', @ptnum+2);
    4. vector4 rot1 = dihedral(@P-pivot, pivot-pos2);
    5.  
    6. vector axis = normalize(cross(set(0,1,0), pos2-pivot));
    7. float ang = ch('ang')*pow(@curveu+0.01,-0.8);
    8. vector4 rot2 = quaternion(ang, axis);
    9.  
    10. vector4 rot = qmultiply(rot2, rot1);
    11.  
    12. p@srot = slerp(set(0,0,0,1), rot, clamp(@Frame-101*@curveu,0,1));
    1. //point层级，此节点之前使用sort节点反向点号
    2. vector prepos = 0;
    3. vector4 prerot = set(0,0,0,1);
    4.  
    5. for(int i=0; i<=@ptnum; i++){
    6.     vector pos = point(0, 'P', i);
    7.     vector pivot = point(0, 'P', i-1);
    8.     prerot = qmultiply(prerot, point(0, 'srot', i));
    9.     pos -= pivot;
    10.     pos = qrotate(prerot, pos);
    11.     pos += prepos;
    12.     prepos = pos;  
    13.     @P = pos;
    14. }

    1. //使用rigdoctor可提取原模型本身旋转后的位移信息
    2. if(@ptnum<@Frame){
    3.     vector pivot = point(0, 'P', @ptnum+1);
    4.     vector pos2 = point(0, 'P', @ptnum+2);
    5.     vector4 rot1 = dihedral(@P-pivot, pivot-pos2);
    6.  
    7.     vector axis1 = point(0, 'tangentv', @ptnum+1);
    8.     vector axis2 = point(0, 'tangentv', @ptnum+2);
    9.     vector4 axisrot = dihedral(axis2, axis1);
    10.  
    11.     vector axis = normalize(cross(set(0,1,0), pos2-pivot));
    12.     float ang = ch('ang')*pow(1-@curveu+0.01,-0.5);
    13.     vector4 rot2 = quaternion(ang, axis);
    14.  
    15.     vector4 rot = qmultiply(axisrot, rot1);
    16.     rot = qmultiply(rot, rot2);
    17.  
    18.     matrix3 m = qconvert(rot);
    19.  
    20.     4@localtransform *= m;
    21. }

    1. //针对原曲线不在同一平面，卷曲后也不再同一平面的问题修正
    2. for(int i=0; i<chi('num'); i++){
    3.     vector pivot = point(0, 'P', i);
    4.     vector prepos =  point(0, 'P', i-1);
    5.     vector nextpos =  point(0, 'P', i+1);
    6.     float ang = ch('ang')*pow(point(0, 'curveu', i)+0.01,-0.8);
    7.     
    8.     vector N = point(0, 'N', i);
    9.     vector preN = point(0, 'N', i-1);
    10.     vector4 prerot = dihedral(preN, N);
    11.     
    12.     vector axis = normalize(cross(N, nextpos-pivot));
    13.     vector4 rot1 = quaternion(ang, axis);
    14.     vector4 rot2 = dihedral(prepos-pivot, pivot-nextpos);
    15.     vector4 rot = qmultiply(rot1, rot2);
    16.  
    17.     for(int j=0; j<i; j++){    
    18.         pos[j] -= pivot;
    19.         pos[j] = qrotate(rot, pos[j]);
    20.         pos[j] = qrotate(prerot, pos[j]);
    21.         pos[j] += pivot;
    22.     }
    23. }
    24.  
    25. for(int i=0; i<chi('num'); i++){
    26.     setpointattrib(0, 'P', i, pos[i]);
    27. }

  • 相关阅读:
    【深度学习】目标检测，Faster-RCNN算法训练，使用mmdetection训练
    Spring循环依赖
    总结C++单例模式
    linux的三剑客
    承包商在工程结算争议里能扭转乾坤的几点
    VM16Pro的Win10虚拟机安装Linux子系统Kali
    浅谈客户端框架设计|一|二|三
    （自我剖析一下我博客“问答”中的第三个问题）准确率一直居低不上是什么原因引起的？
    读书笔记： 如何把一件事做到最好
    如何优雅地校验后端接口数据，不做前端背锅侠
  • 原文地址：https://blog.csdn.net/NapoleonCoder/article/details/134221335