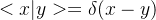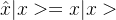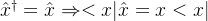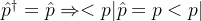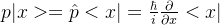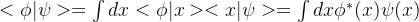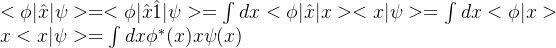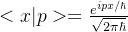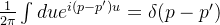-
表象变换与矩阵元
- 表象变换
一维粒子哈密顿量
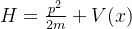
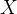 表象中
表象中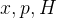 的矩阵元
的矩阵元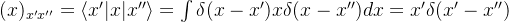
- 态的表象变换
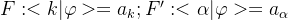
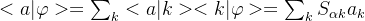
- 不难证明
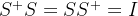
- 算符的表象变换
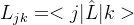
- 坐标表象
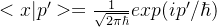
Non-denumerable basis
- 在坐标表象中动量表示为:
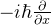
- 坐标在动量表象中表示为:
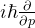
表象变换
- 表象变换就像坐标变换一样可以微操
波函数的变换
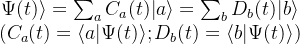
容易证明:
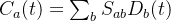
其中:
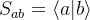
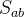 构成变换矩阵
构成变换矩阵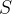
A表象下的波函数C_a B表象下的波函数D_b
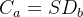
算符的变换
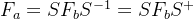
泡利矩阵
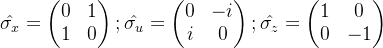
- 泡利矩阵是厄米的
- 泡利算符是单位算符
泡利矩阵的对易关系
![[\sigma_x,\sigma_y]=2i\sigma_z;[\sigma_y,\sigma_z]=2i\sigma_x;[\sigma_z,\sigma_x]=2i\sigma_y](https://1000bd.com/contentImg/2024/03/24/0c42b5f43df4a538.png)
![[\sigma^2,\sigma_x]=[\sigma^2,\sigma_y]=[\sigma^2,\sigma_z]=0](https://1000bd.com/contentImg/2024/03/24/4499b742419a9be4.png)
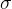 的分量之间满足反对易条件
的分量之间满足反对易条件
- 泡利矩阵的完备性
- 例题
- 自旋1/2的粒子处于态
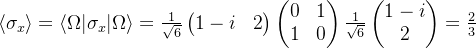
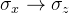 的变换
的变换
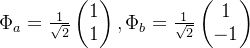
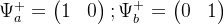
求变换矩阵
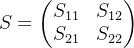
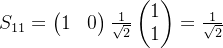
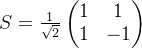
- 任意态
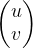
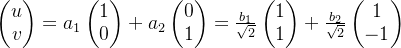
那么:
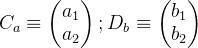
那么波函数变换就是:
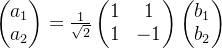
那么算符变换就是:
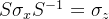
习题解答
- 动量表象中角动量
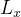 的矩阵元和
的矩阵元和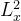 的矩阵元
的矩阵元
动量算符的本征函数
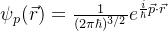
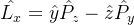
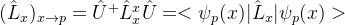

- 线性谐振子哈密顿量在动量表象中的矩阵元

设已知在
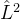 和
和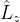 的共同表象中,算符
的共同表象中,算符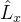 和
和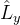 的矩阵分别为
的矩阵分别为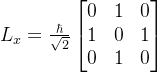
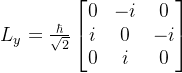
求它的本征值和归一化的本征函数。最后将矩阵对角化


-
相关阅读:
EasyNLP中文文图生成模型带你秒变艺术家
go 稀疏数组
NTP时间同步服务器设置
R语言使用lm函数构建线性回归模型、应用回归模型预测新的预测变量对应的响应变量(predict函数返回预测值的向量)
余弦相似度算法进行客户流失分类预测
青少年软件编程(202209)(C语言)等级考试(五级)试题及参考答案
【Superset3.0】更全面superset相关--配置邮件报告发送: 附件乱码以及导出文件(截屏图片)中文乱码问题
Socks5代理:数字时代的通行证
rename 批量修改文件名简单用法
K8s复习笔记8--结合pv/pvc Mysql 主从架构
- 原文地址:https://blog.csdn.net/Chandler_river/article/details/134192975