-
【数据结构】树与二叉树(四):满二叉树、完全二叉树及其性质
5.1 树的基本概念
5.1.1 树的定义
- 一棵树是结点的有限集合T:
- 若T非空,则:
- 有一个特别标出的结点,称作该树的根,记为root(T);
- 其余结点分成若干个不相交的非空集合T1, T2, …, Tm (m>0),其中T1, T2, …, Tm又都是树,称作root(T)的子树。
- T 空时为空树,记作root(T)=NULL。
- 若T非空,则:
5.1.2 森林的定义
一个森林是0棵或多棵不相交(非空)树的集合,通常是一个有序的集合。换句话说,森林由多个树组成,这些树之间没有交集,且可以按照一定的次序排列。在森林中,每棵树都是独立的,具有根节点和子树,树与树之间没有直接的连接关系。
森林是树的扩展概念,它是由多个树组成的集合。在计算机科学中,森林也被广泛应用于数据结构和算法设计中,特别是在图论和网络分析等领域。

5.1.3 树的术语
- 父亲(parent)、儿子(child)、兄弟(sibling)、后裔(descendant)、祖先(ancestor)
- 度(degree)、叶子节点(leaf node)、分支节点(internal node)
- 结点的层数
- 路径、路径长度、结点的深度、树的深度
参照前文:【数据结构】树与二叉树(一):树(森林)的基本概念:父亲、儿子、兄弟、后裔、祖先、度、叶子结点、分支结点、结点的层数、路径、路径长度、结点的深度、树的深度
5.1.4 树的表示
5.2 二叉树
5.2.1 二叉树
1. 定义
二叉树是一种常见的树状数据结构,它由结点的有限集合组成。一个二叉树要么是空集,被称为空二叉树,要么由一个根结点和两棵不相交的子树组成,分别称为左子树和右子树。每个结点最多有两个子结点,分别称为左子结点和右子结点。

2. 特点
二叉树的特点是每个结点最多有两个子结点,并且子结点的位置是有序的,即左子结点在前,右子结点在后。这种有序性使得二叉树在搜索、排序等算法中有广泛的应用。
-
在二叉树中,根结点是整个树的起始点,通过根结点可以访问到整个树的其他结点。每个结点都可以看作是一个独立的二叉树,它的左子树和右子树也是二叉树。
-
二叉树可以是空树,也可以是只有根结点的树,或者是由多个结点组成的树。每个结点可以包含一个数据元素,以及指向左子结点和右子结点的指针。
-
二叉树的形状可以各不相同,它可以是平衡的或者不平衡的,具体取决于结点的分布情况。在二叉树中,每个结点的左子树和右子树都是二叉树,因此可以通过递归的方式来处理二叉树的操作。
3. 性质
引理5.1:二叉树中层数为i的结点至多有 2 i 2^i 2i个,其中 i ≥ 0 i \geq 0 i≥0。
引理5.2:高度为k的二叉树中至多有 2 k + 1 − 1 2^{k+1}-1 2k+1−1个结点,其中 k ≥ 0 k \geq 0 k≥0。
引理5.3:设T是由n个结点构成的二叉树,其中叶结点个数为 n 0 n_0 n0,度数为2的结点个数为 n 2 n_2 n2,则有 n 0 = n 2 + 1 n_0 = n_2 + 1 n0=n2+1。
详细证明过程见前文:【数据结构】树与二叉树(三):二叉树的定义、特点、性质及相关证明
4. 满二叉树
定义
定义5.3:一棵非空高度为 k ( k ≥ 0 ) k( k≥0) k(k≥0)的满二叉树(perfect binary tree),是有 2 k + 1 − 1 2^{k+1}-1 2k+1−1个结点的二叉树。
特点
满二叉树是一种特殊类型的二叉树,具有以下特点:
-
叶结点都在第 k k k层上:满二叉树的高度为 k k k,即最深层的层数为 k k k。所有的叶结点都位于最深层,也就是第 k k k层。
-
每个分支结点都有两个子结点:满二叉树中的每个非叶结点都有两个子结点。也就是说,每个结点要么是叶结点,要么有两个子结点。
-
叶结点的个数等于非叶结点个数加1:满二叉树中的叶结点个数(记为 n 0 n_{0} n0)与非叶结点个数(记为 n 1 n_{1} n1)之间满足关系 n 0 = n 1 + 1 n_{0} = n_{1} + 1 n0=n1+1。也就是说,叶结点的个数比非叶结点的个数多1。
根据定义5.3,一棵非空高度为 k k k的满二叉树具有 2 k + 1 − 1 2^{k+1} - 1 2k+1−1个结点。这个结论可以通过归纳法证明。当 k = 0 k=0 k=0时,满二叉树只有一个结点,符合条件。假设对于某个正整数 k k k,高度为 k k k的满二叉树有 2 k − 1 2^{k} - 1 2k−1个结点。那么对于高度为 k + 1 k+1 k+1的满二叉树,根结点有两个子结点,每个子结点都是高度为 k k k的满二叉树。根据归纳假设,每个子树都有 2 k − 1 2^{k} - 1 2k−1个结点,所以总共有 2 ⋅ ( 2 k − 1 ) + 1 = 2 k + 1 − 1 2 \cdot (2^{k} - 1) + 1 = 2^{k+1} - 1 2⋅(2k−1)+1=2k+1−1个结点。因此,高度为 k + 1 k+1 k+1的满二叉树有 2 k + 1 − 1 2^{k+1} - 1 2k+1−1个结点。(引理5.2)
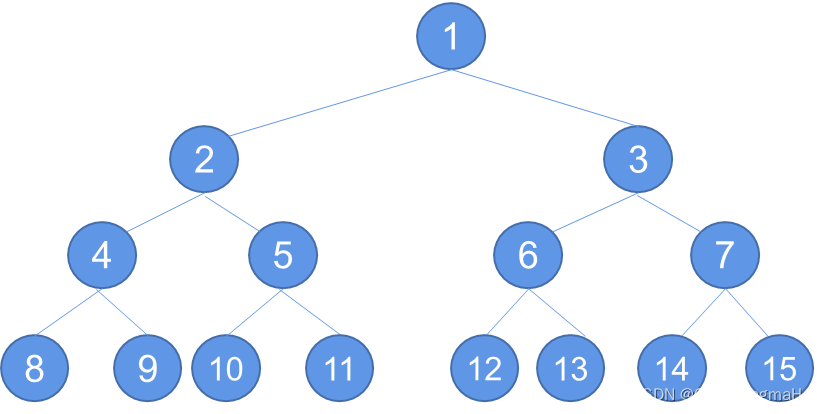
可按层次顺序(即按从第0层到第k层,每层由左向右的次序)将一棵满二叉树的所有结点用自然数从1开始编号。例如:1 / \ 2 3 / \ / \ 4 5 6 7 /\ /\ /\ /\ 8 9 A B C D E- 1
- 2
- 3
- 4
- 5
- 6
- 7
根据上述满二叉树的编号规律,节点的编号如下:
第0层:1 第1层:2, 3 第2层:4, 5, 6, 7 第3层:8, 9, A, B, C, D, E- 1
- 2
- 3
- 4
这里使用了十六进制数字A到E来表示编号大于9的节点。这样,高度为3的满二叉树的所有节点共有 2 4 − 1 = 15 2^4-1=15 24−1=15个节点,按照层次顺序从1到15进行编号。
5. 完全二叉树
定义
定义5.4:一棵包含 n n n个节点、高度为 k k k的二叉树 T T T,当按层次顺序编号 T T T的所有节点,对应于一棵高度为 k k k的满二叉树中编号由1至 n n n的那些节点时, T T T被称为完全二叉树(complete binary tree)。
换句话说,完全二叉树是按照层次顺序从左到右依次填满节点的二叉树,除了最后一层可能不满外,其他层都必须是满的。在完全二叉树中,节点编号与高度为 k k k的满二叉树中的节点编号一一对应。
下面是一个例子来说明完全二叉树的概念:
1 / \ 2 3 / \ / 4 5 6- 1
- 2
- 3
- 4
- 5
在上面的例子中,这棵二叉树有6个节点,高度为2。按照层次顺序编号,节点的编号与高度为2的满二叉树中的节点编号一一对应。完全二叉树在树的存储和遍历等操作中具有一些特殊的性质,因此在算法和数据结构中经常被使用。
特点
- 树中只有最下面两层节点的度可以小于2
- 这意味着在完全二叉树中,除了最后一层和倒数第二层的节点可以是度小于2的节点(即叶节点或只有一个子节点),其他层的节点都必须是度为2的节点(具有两个子节点)。
- 树中最下面一层的节点都集中在该层最左边的若干位置上(满二叉树意义上)
- 在完全二叉树中,最后一层的节点从左到右依次排列,不会有空缺。
- 树中叶节点只能在层数最大的两层上出现,即存在一个非负整数
k
k
k使得树中每个叶节点或在第
k
k
k层或第
k
+
1
k+1
k+1层上
- 这意味着在完全二叉树中,叶节点只能出现在最底层和倒数第二层上。其他层不会有叶节点。
- 对树中所有节点,按层次顺序,用自然数从1开始编号,仅编号最大的非叶节点可以没有右儿子,其余非叶节点都有两个儿子节点
- 在完全二叉树中,除了编号最大的非叶节点可能只有一个子节点(左子节点),其他非叶节点都必须有两个子节点(左子节点和右子节点)。
- 树中所有节点对应于高度为
k
k
k的满二叉树中编号由1至
n
n
n的那些节点:
- 这是完全二叉树的定义,完全二叉树的节点编号与高度为 k k k的满二叉树中的节点编号一一对应。
这些特点描述了完全二叉树的一些重要性质和规律。完全二叉树在算法和数据结构中经常被使用,因为它的结构相对简单,可以方便地进行存储和遍历等操作。
引理5.4
将一棵有 n n n个节点的完全二叉树按层次顺序用自然数从1开始编号时,节点编号 i i i的结点满足的性质:
① 若 i ≠ 1 i\neq1 i=1,则编号为 i i i的结点的父节点的编号为 ⌊ i / 2 ⌋ \lfloor i/2 \rfloor ⌊i/2⌋。即除了根节点(编号为1)之外,其他节点的父节点的编号可以通过将节点编号除以2并向下取整得到。
② 若 2 i ≤ n 2i\leq n 2i≤n,则编号为 i i i的结点的左子节点的编号为 2 i 2i 2i。这意味着如果节点编号的两倍小于等于总节点数 n n n,则该节点有左子节点,且左子节点的编号为节点编号的两倍。
③ 若 2 i + 1 ≤ n 2i+1\leq n 2i+1≤n,则编号为 i i i的结点的右子节点的编号为 2 i + 1 2i+1 2i+1。这意味着如果节点编号的两倍加一小于等于总节点数 n n n,则该节点有右子节点,且右子节点的编号为节点编号的两倍加一。
这些性质描述了完全二叉树中节点编号与父节点、左子节点和右子节点编号之间的关系。通过这些性质,可以方便地在完全二叉树中定位和访问特定节点的父节点、左子节点和右子节点。
证明完全二叉树性质②的正确性可以通过归纳法进行:
-
首先,当 i = 1 i=1 i=1时,如果 n ≥ 2 n\geq2 n≥2,则左儿子的编号显然为2。这是基本情况。
-
假设对于所有 1 ≤ j ≤ i 1\leq j\leq i 1≤j≤i,且 2 i ≤ n 2i\leq n 2i≤n,节点 j j j的左儿子的编号为 2 j 2j 2j。现在要证明节点 j = i + 1 j=i+1 j=i+1的左儿子的编号为 2 ( i + 1 ) 2(i+1) 2(i+1)。
-
根据完全二叉树的性质,如果 2 ( i + 1 ) ≤ n 2(i+1)\leq n 2(i+1)≤n,则节点 i + 1 i+1 i+1有左儿子。根据层次顺序的编号规则,节点 i + 1 i+1 i+1的左儿子之前的两个节点就是节点 i i i的左儿子和右儿子。根据归纳假设,节点 i i i的左儿子编号为 2 i 2i 2i,因此节点 i i i的右儿子编号为 2 i + 1 2i+1 2i+1。因此,节点 i + 1 i+1 i+1的左儿子的编号为 2 i + 2 = 2 ( i + 1 ) 2i+2=2(i+1) 2i+2=2(i+1)。
-
通过归纳法,我们证明了对于所有 1 ≤ i ≤ n 1\leq i\leq n 1≤i≤n,若 2 i ≤ n 2i\leq n 2i≤n,则节点 i i i的左儿子的编号为 2 i 2i 2i。
由于性质②可以直接推导出性质③,而性质②和③又可以得到性质①,所以这个证明也同时证明了性质③和①。
引理5.5 具有n个结点的完全二叉树的高度是⌊𝑙𝑜𝑔2𝑛⌋ .
证明:
设完全二叉树的高度为 k k k。根据定义5.4,完全二叉树的结点个数介于高度为 k k k和 k − 1 k-1 k−1的满二叉树的结点数之间,即有 2 k − 1 < n ≤ 2 k + 1 − 1 2^k - 1 < n \leq 2^{k+1} - 1 2k−1<n≤2k+1−1。从而,我们可以得到 2 k ≤ n ≤ 2 k + 1 − 1 2^k \leq n \leq 2^{k+1} - 1 2k≤n≤2k+1−1,即 k ≤ log 2 n < k + 1 k \leq \log_2 n < k+1 k≤log2n<k+1。
由于高度 k k k为整数,所以我们可以得到 k = ⌊ log 2 n ⌋ k = \lfloor \log_2 n \rfloor k=⌊log2n⌋。
因此,具有 n n n个结点的完全二叉树的高度是 ⌊ log 2 n ⌋ \lfloor \log_2 n \rfloor ⌊log2n⌋。
思考:完全二叉树和满二叉树是什么关系?
- 一棵树是结点的有限集合T:
-
相关阅读:
如何在三星手机上截屏?每一款三星手机的每一种方法,包括S23
Maven快速配置和入门
计算机视觉40例之案例08石头剪刀布手势识别
SpringBoot 使用过滤器修改请求参数
Redis学习
【前端Vue3】——JQuery知识点总结(超详细)
破局DevOps|8大北极星指标指引研发效能方向
【MySQL】的存储引擎 事务 锁机制 日志
基于SSM的传统文化网站
【MRC转化为ARC Objective-C语言】
- 原文地址:https://blog.csdn.net/m0_63834988/article/details/134253611