[动态规划] (十一) 简单多状态 LeetCode 面试题17.16.按摩师 和 198.打家劫舍

[动态规划] (十一) 简单多状态: LeetCode 面试题17.16.按摩师 和 198.打家劫舍

注：本题与打家劫舍基本一样，所以只写一道按摩师，末尾只会加上打家劫舍1的代码。

面试题 17.16. 按摩师
198. 打家劫舍

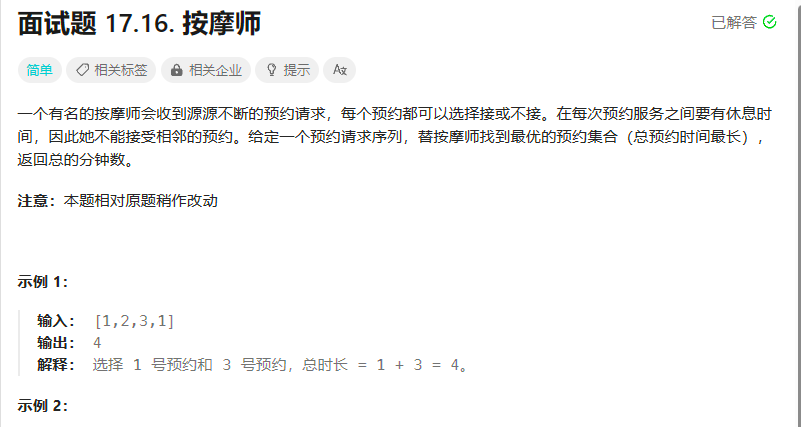
题目分析

(1) 按摩师不能连续接预约

(2) 按摩师可以选择接或者不接预约

(3) 返回预约时间最长的分钟数

题目解析

状态表示

dp[i]：按往常的经验，以i为结尾的最大的服务的分钟数

dp[i]又可以分为：

• f[i]：到i位置，接第i次预约的服务的最大分钟数
• g[i]：到i位置，不接第i次预约的服务的最大分钟数

状态转移方程

• f[i]:

f[i]是到i位置，必须接i位置的服务的最大分钟数。

由于不能连续接受服务，所以接了i位置，i-1位置就不能接受预约了。

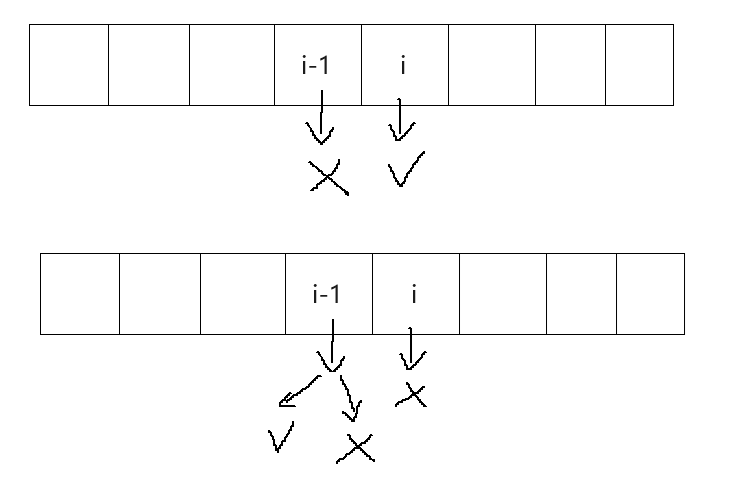
g[i-1]正好是到i-1位置且不接受i-1预约的最大分钟数，再加上对应的i位置的分钟数就是f[i]。(可以参考后面的图)

f[i] = g[i-1] + nums[i]
1

• g[i]:

g[i]是到i位置，不接i位置的服务的最大分钟数。

由于不接i位置，所以只能看i-1位置。而i-1位置也分为接或者不接。

接i-1位置为f[i-1] (参考状态表示)，不接i-1为g[i-1] (参考状态表示)。

由于求最大值，取它们两个较大的值即可。(可以参考后面的图)

g[i] = max(f[i-1], g[i-1])
1

初始化和填表顺序

• 初始化
• 访问i-1，所以一般初始化前面的位置。

i == 0时，参考状态表示

f[0] = nums[0], g[0] = 0
1

• 填表顺序

从左向右填表。

看到这里，大家可以尝试实现代码，再来看接下来的内容。

---

代码实现

按摩师

class Solution {
public:
    int massage(vector<int>& nums) {
        //创建dp数组
        int n = nums.size();
        if(n == 0) return 0;
        vector<int> f(n);//选到i位置，必选i
        vector<int> g(n);//选到i位置，不选i
        //初始化
        f[0] = nums[0], g[0] = 0;
        //填表
        for(int i = 1; i < n; i++)
        {
            g[i] = max(f[i-1], g[i-1]);
            f[i] = g[i-1] + nums[i];
        }
        //返回值
        return max(g[n-1], f[n-1]);
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

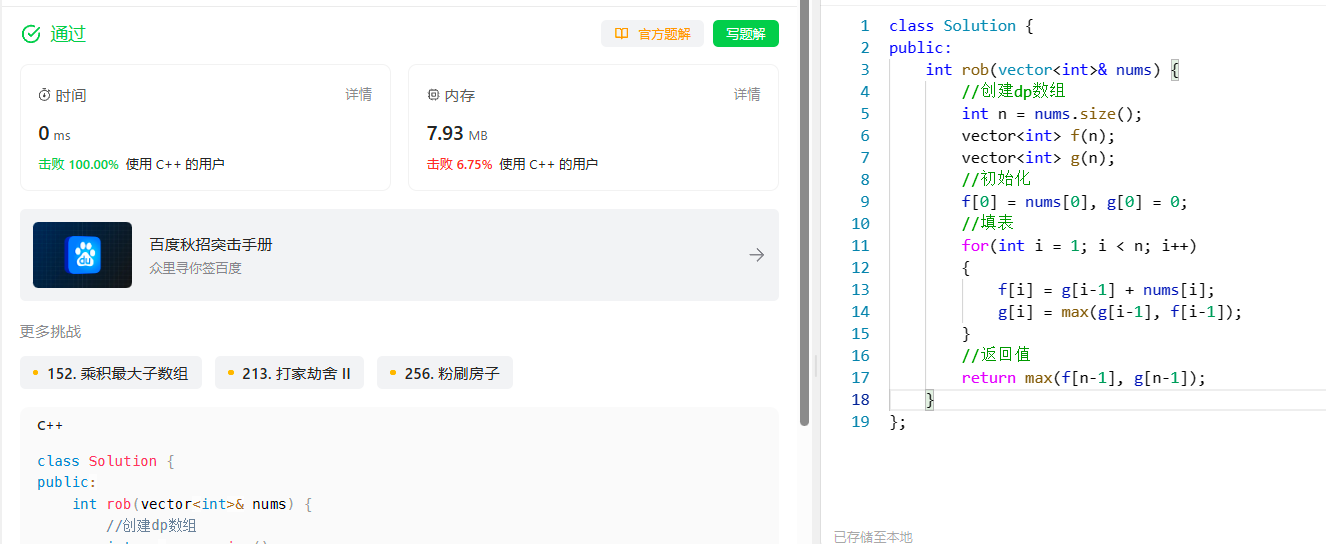
打家劫舍

class Solution {
public:
    int rob(vector<int>& nums) {
        //创建dp数组
        int n = nums.size();
        vector<int> f(n);
        vector<int> g(n);
        //初始化
        f[0] = nums[0], g[0] = 0;
        //填表
        for(int i = 1; i < n; i++)
        {
            f[i] = g[i-1] + nums[i];
            g[i] = max(g[i-1], f[i-1]);
        }
        //返回值
        return max(f[n-1], g[n-1]);
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

总结

细节：注重将问题细分，加上画图理解即可。