【电路笔记】-串联RLC电路分析

串联RLC电路分析

电阻器 ®、电感器 (L) 和电容器 © 是电子器件中的三个基本无源元件。 它们的属性和行为已在交流电阻、交流电感和交流电容文章中详细介绍。

在本文中，我们将重点讨论这三个组件的串联组合（称为串联 RLC 电路）。 首先，演示部分总结了三个组成组件的交流行为，并简要介绍了 RLC 电路。

在第二部分中，我们讨论该电路在直流电压阶跃下的电气行为，并强调为什么这种特定响应很重要。

接下来，我们在第三部分中通过计算和绘制 RLC 电路的传递函数来重点关注 RLC 电路的交流响应。

最后，我们通过在彼此之间切换组件来提出 RLC 电路的两种替代方案，我们看到交流响应变得完全不同。

1、概述

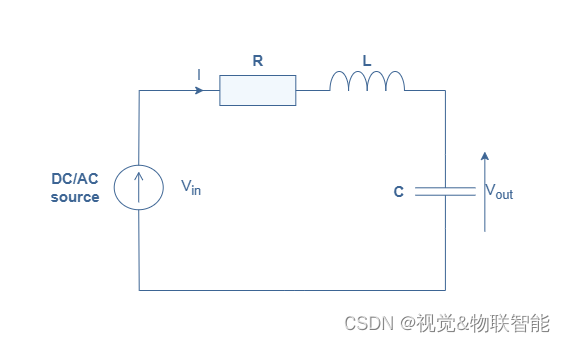
下面的图 1 给出了 RLC 电路的表示：

图1：RLC串联电路示意图

该电阻器是纯电阻元件，其两端的电压和电流之间不存在相移。 其阻抗 ($Z_R$) 在直流和交流状态下保持相同，等于 $R$（以 $\Omega$ 为单位）。

电感器是纯电抗元件，相移为 +90° 或 $+\pi /2$ rad。 其阻抗由 $Z_L=j\omega L$ 给出，其中 $\omega$ 是交流情况下电压/电流的角脉动，L 是电感（以 $H$ 为单位）。 在直流状态下，电感器表现为两个端子之间的短路，而在交流状态下，当阻抗随频率增加时，电感器会变成开路。

电感器通常被视为抵抗电流变化的组件。

电容器也是纯电抗元件，但其相移为-90°或$-\pi /2$ rad。 其阻抗由 $Z_C=-j/C\omega$ 给出，其中 $C$ 为电容（以 $F$ 为单位），因此当频率增加时，它在直流状态下表现为开路，在交流状态下表现为短路。

电容器通常被视为抵抗电压变化的组件。

在图 1 中，这三个组件串联互连。 该电路由直流或交流电源供电，输出是电容器两端的电压。 电路的总阻抗是前面所述的独立阻抗的总和：

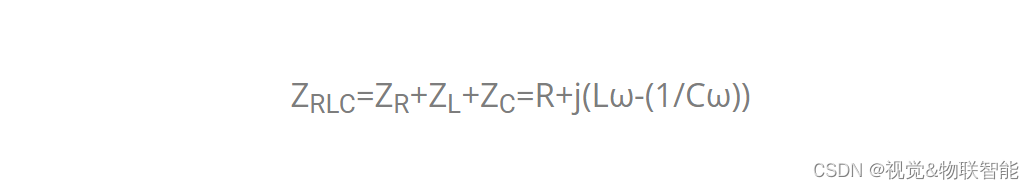
在下一节中，我们将介绍该电路对电压阶跃的响应，也称为瞬态响应。

2、瞬态响应

在本节中，我们将重点关注图 1 中所示电路在应用 Heaviside 步骤 $H(t)$ 时的行为：

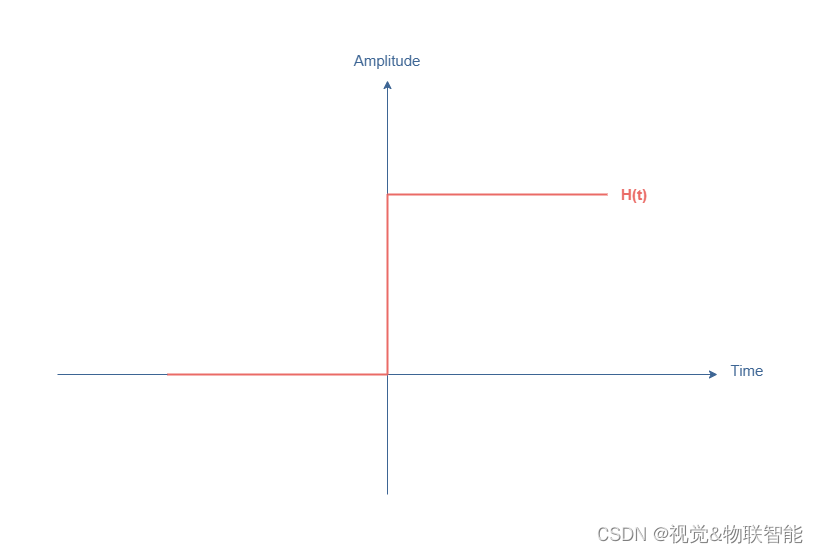
图2：海维赛德(Heaviside)函数

Heaviside 步骤的特征是，$t<0$ 时等于 0，$t>0$ 时等于 $V_{in}$。 这两种状态之间的转换类似于脉冲，因为当 $t=0$ 时导数趋向于 $+\infty$。

通过对电路进行网格分析，我们可以写出 $V_{in}=R\times I+L\times$