快速排序——及其改进

1. hoare版本（原始版本）：
   思想：树的遍历思想，先把数组第一个数作为KEY,然后left从左到右，right从右到左一起走，当left找到比key大的值时停下来，当right找到比key小的值时停下来，交换两个值，继续走，最后当left=right的时候，left处的值和key交换，这是的key的值就处于正确位置，然后利用树遍历的思想，分别这样递归排左边右边，最后结束时，整个数组就排好了。
   代码思路：先写单趟，在写整体

单趟：

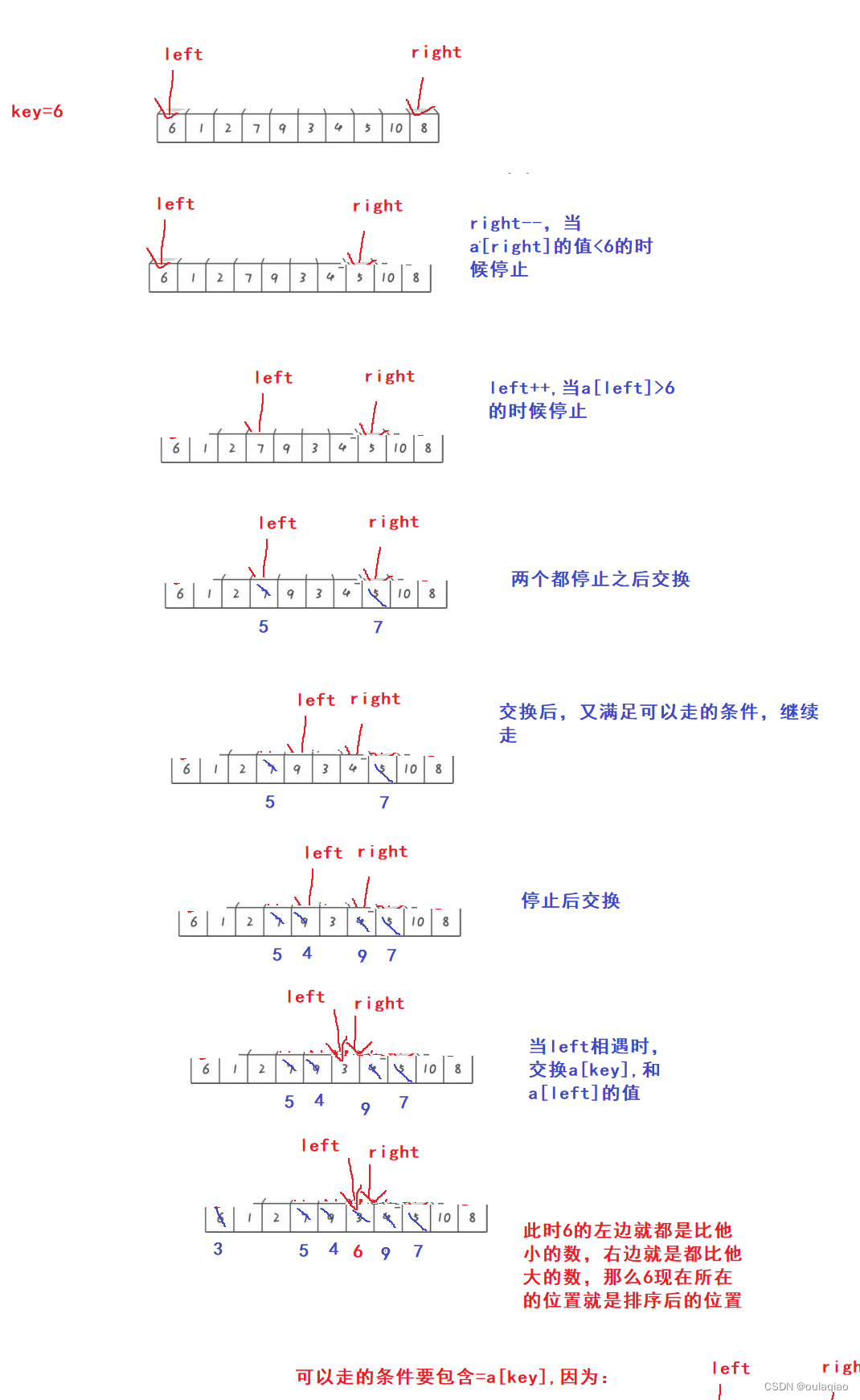
特殊细节分析

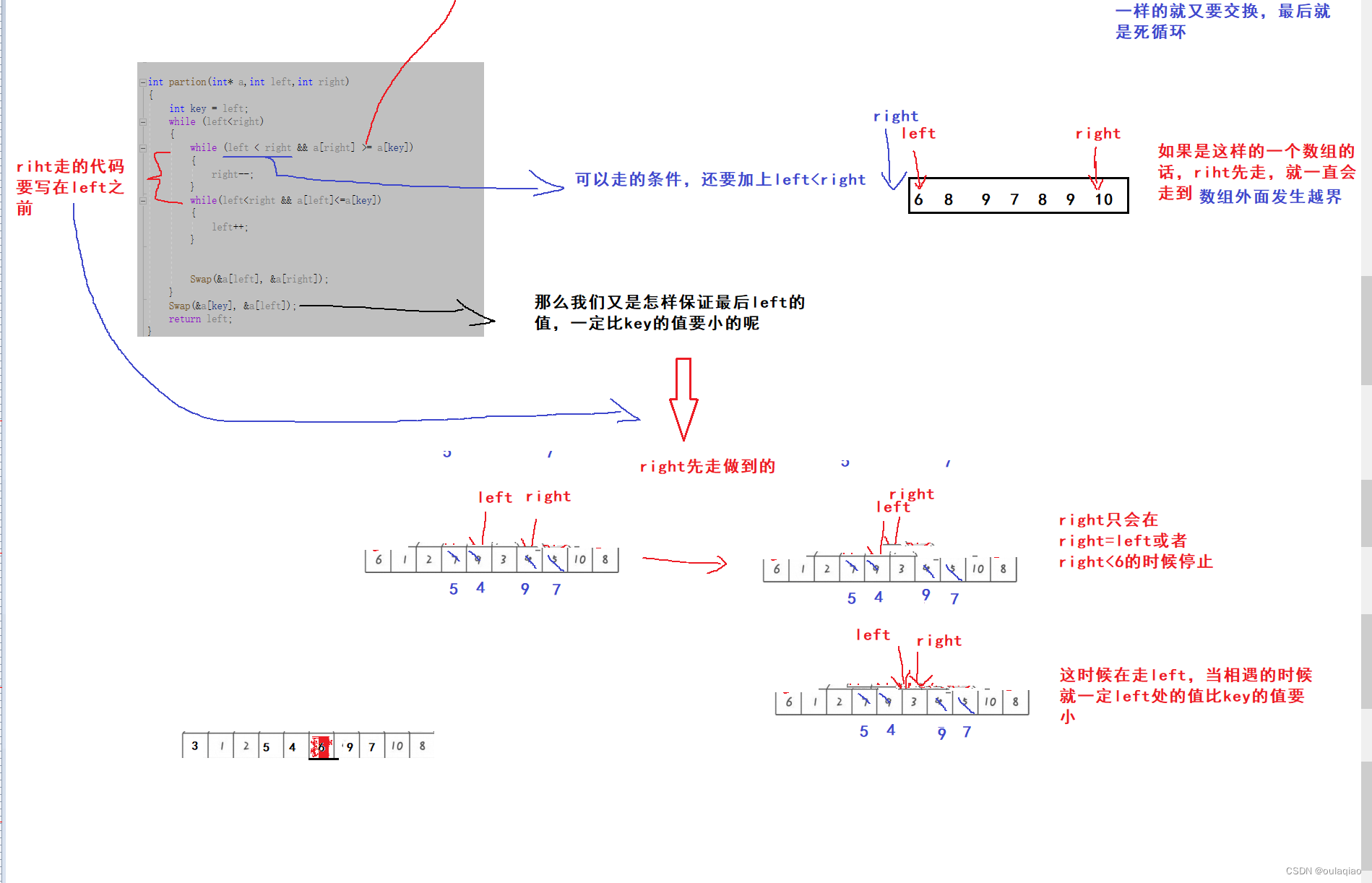
int partion(int* a,int left,int right)
{
	int key = left;
	while (left<right)
	{
		while (left < right && a[right] >= a[key])
		{
			right--;
		}
		while(left<right && a[left]<=a[key])
		{
			left++;
		}

		
		Swap(&a[left], &a[right]);
	}
	Swap(&a[key], &a[left]);
	return left;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

这是是单趟的代码，写到这里只可以把key的值放到了有序后他所在的值，他的左右两边的值还是无序的，那么我们又该如何让左右两边的值都变的有序呢，这里就用到了二叉树递归遍历的思想（根 左 右）

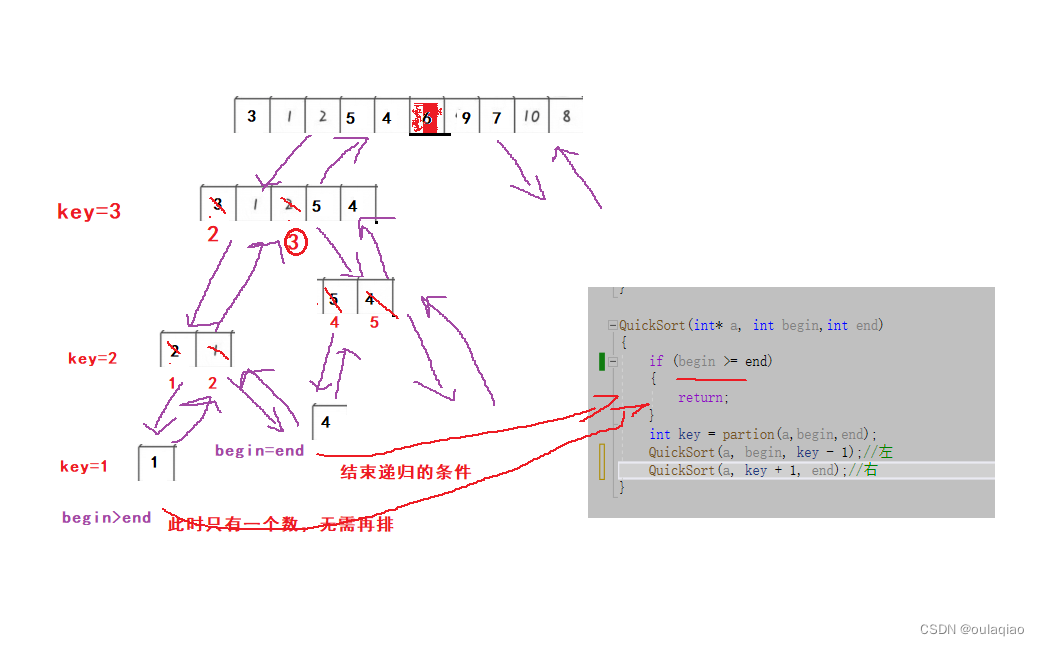
QuickSort(int* a, int begin,int end)
{
	if (begin >= end)
	{
		return;
	}
	int key = partion(a,begin,end);
	QuickSort(a, begin, key - 1);//左
	QuickSort(a, key + 1, end);//右
}
1
2
3
4
5
6
7
8
9
10

可以看出，在乱序的时候的时间效率是很高的O(logN*N),但是如果在有序或者接近有序就很慢O（N^2）：

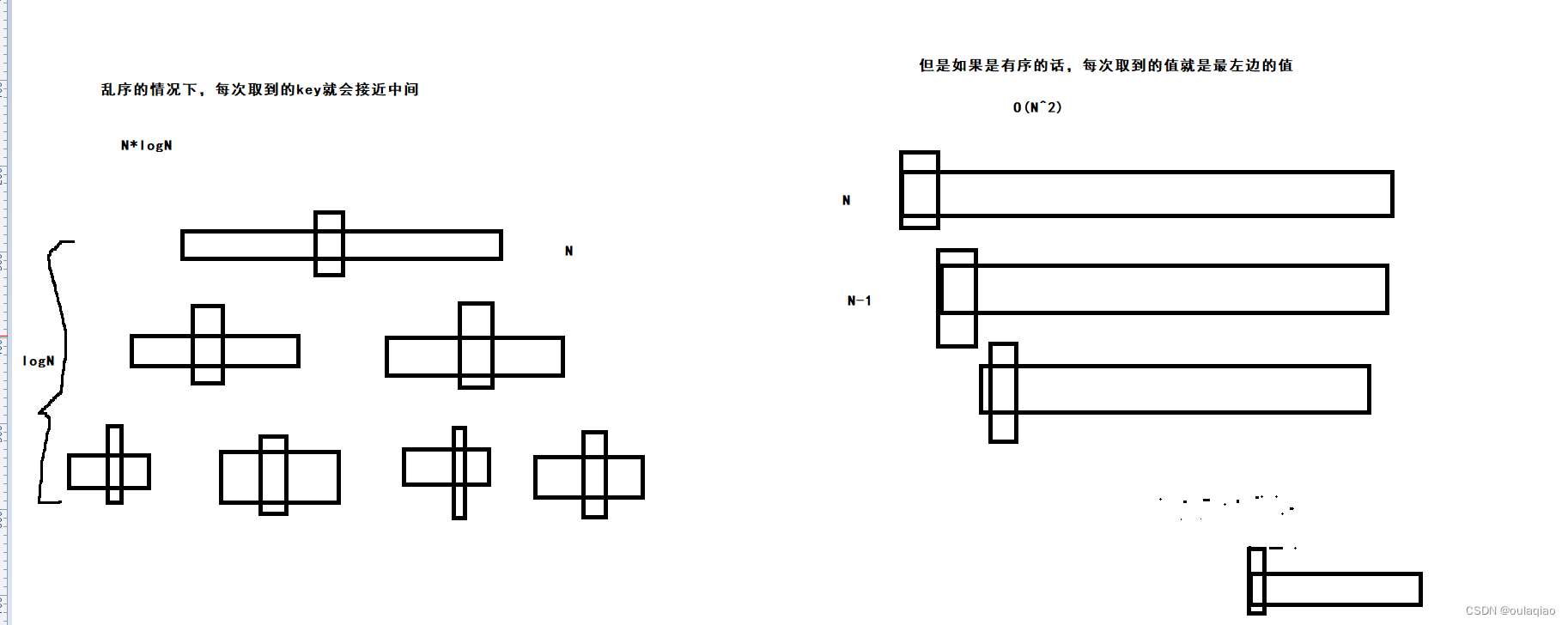
为了避免这种情况，每次取key的时候，就不能直接取最左边的那个，要取left right 和他们之间的那个，这三个数中大小为中的那个值(三数取中）：

int GetMidd(int* a, int left, int right)
{
	int midi = (left + right) / 2;
	if (a[left] < a[midi])
	{
		if (a[midi] < a[right])
			return midi;
		else if (a[left] > a[right])
		{
			return left;
		}
		else
		{
			return right;
		}
	}
	else//(a[left] > a[midi]
	{
		if (a[midi] > a[right])
		{
			return midi;
		}
		else if (a[left] < a[right])
		{
			return left;
		}
		else
		{
			return right;
		}
	}
}



int partion(int* a,int left,int right)
{
	int mid = GetMidd(a,left,right);
	Swap(&a[mid], &a[left]);
	int key = left;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

改进：（坑位法：）

int partion2(int* a, int left, int right)
{
	int mid = GetMidd(a, left, right);
	Swap(&a[mid], &a[left]);
	//保存key的值后，在左边形一个坑位
	int key = a[left];
	int hold = left;
	while (left < right)
	{
		//右边先走，找小，找到后，填到左边的坑位，形成右边的新坑位
		while (left < right && a[right] >= key)
		{
			right--;
		}
		a[hold] = a[right];
		hold = right;
		//走左边，找大，找到后，填到右边的坑位，形成左边的新坑位

		while (left < right && a[left] <= key)
		{
			left++;
		}
		a[hold] = a[left];
		hold = left;
	}
	a[hold] = key;
	return hold;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

改进：（指针法：）
cur找小，找到小,pre++,交换cur和pre的值，

int partion3(int* a, int left, int right)
{

	int mid = GetMidd(a, left, right);
	Swap(&a[mid], &a[left]);
	int key = left;
	int cur = left+1;
	int pre = left;
	/*while (cur <= right)
	{
		while (cur <= right && a[cur] >= a[key])
		{
			cur++;

		}
		if (cur > right)
		{
			break;
		}
		pre++;
		Swap(&a[cur], &a[pre]);
		cur++;

	}
	Swap(&a[left], &a[pre]);
	return pre;*/
	while (cur <= right)
	{
		if (a[cur] < a[key] && ++pre != cur)
		{
			Swap(&a[cur], &a[pre]);

		}
		cur++;
	}
	Swap(&a[left], &a[pre]);
	return pre;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

非递归法——用栈的后进先出原则，保存他的递归节点

void QuickSortNoNS(int* a,int begin,int end)
{
	ST st;
	STInit(&st);
	STPush(&st, end);
	STPush(&st, begin);
	while (!STEmpty(&st))
	{
		int left = STTop(&st);//取栈顶元素
		STPop(&st);
		int right = STTop(&st);
		STPop(&st);

		int key = partion(a, left, right);
		if (key+1 < right)//入栈
		{
			STPush(&st, right);
			STPush(&st, key + 1);
		}
		if (key - 1 > left)
		{

			STPush(&st, key-1);
			STPush(&st, left);
		}

	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28