LeetCode：1465. 切割后面积最大的蛋糕（C++)

目录

1465. 切割后面积最大的蛋糕

题目描述：

实现代码与解析：

贪心

原理思路：

---

1465. 切割后面积最大的蛋糕

题目描述：

        矩形蛋糕的高度为 h 且宽度为 w，给你两个整数数组 horizontalCuts 和 verticalCuts，其中：

•  horizontalCuts[i] 是从矩形蛋糕顶部到第  i 个水平切口的距离
• verticalCuts[j] 是从矩形蛋糕的左侧到第 j 个竖直切口的距离

请你按数组 horizontalCuts 和 verticalCuts 中提供的水平和竖直位置切割后，请你找出 面积最大 的那份蛋糕，并返回其 面积 。由于答案可能是一个很大的数字，因此需要将结果 对 109 + 7 取余 后返回。

示例 1：

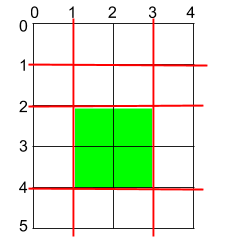
输入：h = 5, w = 4, horizontalCuts = [1,2,4], verticalCuts = [1,3]
输出：4 
解释：上图所示的矩阵蛋糕中，红色线表示水平和竖直方向上的切口。切割蛋糕后，绿色的那份蛋糕面积最大。

示例 2：

输入：h = 5, w = 4, horizontalCuts = [3,1], verticalCuts = [1]
输出：6
解释：上图所示的矩阵蛋糕中，红色线表示水平和竖直方向上的切口。切割蛋糕后，绿色和黄色的两份蛋糕面积最大。

示例 3：

输入：h = 5, w = 4, horizontalCuts = [3], verticalCuts = [3]
输出：9

实现代码与解析：

贪心

class Solution {
public:
    int mod = 1e9 + 7;
    int maxArea(int h, int w, vector<int>& horizontalCuts, vector<int>& verticalCuts) {
 
        sort(horizontalCuts.begin(), horizontalCuts.end());
        sort(verticalCuts.begin(), verticalCuts.end());
 
        int maxh = horizontalCuts[0] - 0;
        int maxw = verticalCuts[0] - 0;
        for (int i = 1; i < horizontalCuts.size(); i++) {
            maxh = max(horizontalCuts[i] - horizontalCuts[i - 1], maxh);
        }
 
        for (int i = 1; i < verticalCuts.size(); i++) {
            maxw = max(verticalCuts[i] - verticalCuts[i - 1], maxw);
        }
 
        maxh = max(h - horizontalCuts[horizontalCuts.size() - 1], maxh);
        maxw = max(w - verticalCuts[verticalCuts.size() - 1], maxw);
        return (int)((long long)maxw * maxh % mod);
    }
};

原理思路：

        找出横向与纵向的最大差值相乘即可，注意边界。