CS224W1.3——图表示的选择

这小节主要讲图表示的选择。

1. 图网络构成

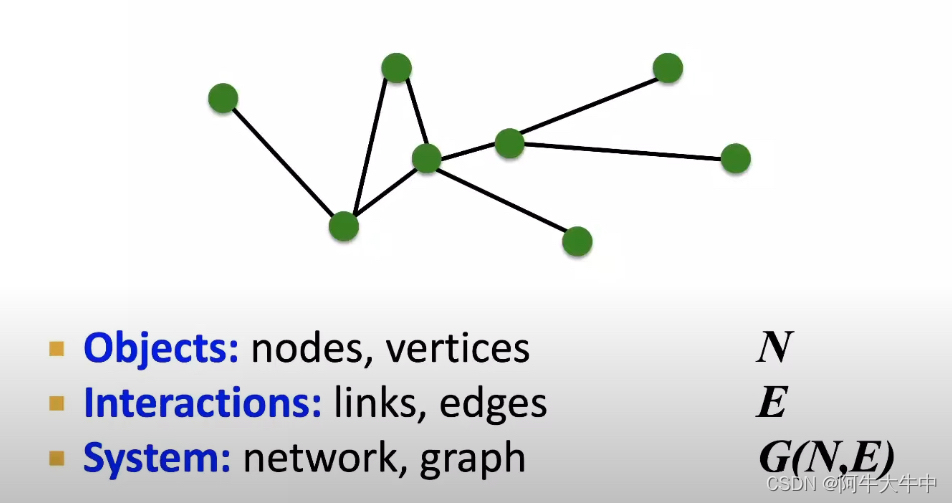
对于每个实体，我们创建节点$N$，对于每个关系，我们创建边$E$，对于整体而言，我们创建图$G(N,E)$

图的重要之处在于它是一种通用语言，比如：

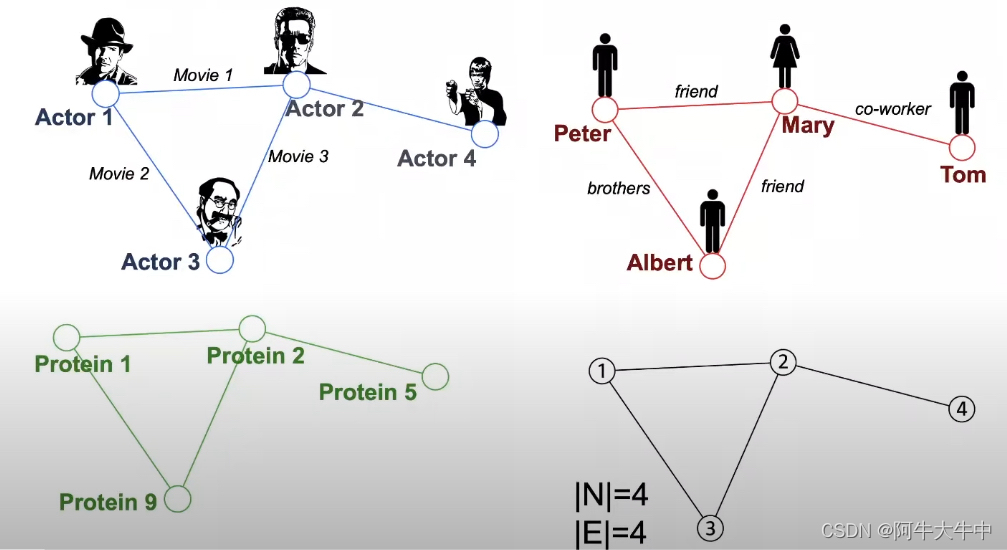
在上图前三种不同场景中，用的图结构其实是一致的。

2. 选择一个合适的表示

你选择的节点数据和边数据是十分重要的。

选择合适的网络表示给定领域或给定问题，将决定我们成功使用网络的能力。

3. 图结构实例

下面是一个无向图与有向图的示例：

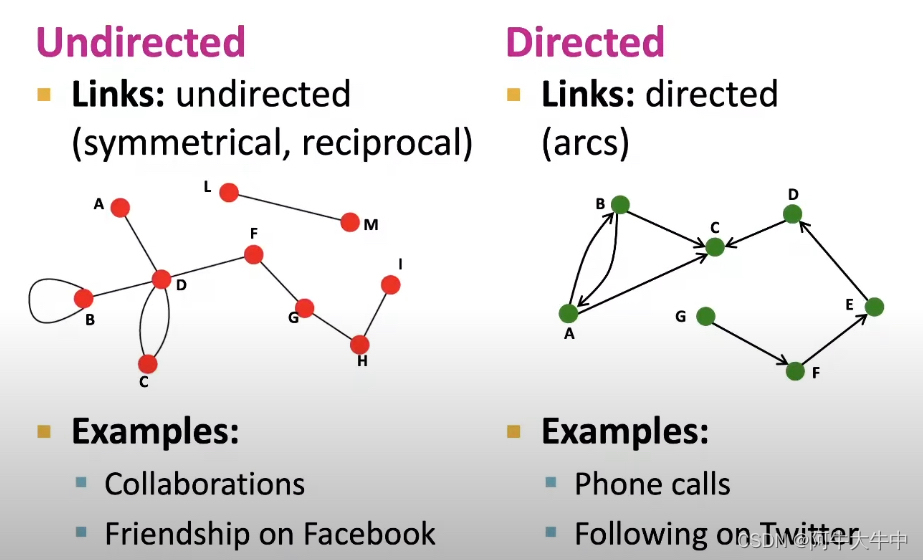
• 无向图可以是合作关系、或一些朋友关系。
• 有向图可以是电话记录，粉丝关系等。

下面是一些无向图的度，有向图的度解释：

3.1 二部图

二部图是一种在不同领域都很常见的图结构。

二部图的特点是通常是由两种不同类型的节点组成的图，其中节点只与其他类型的节点交互。

我们可以定义折叠（folded）或映射（projected）网络概念，比如作者合作网络，电影评分网络，举个例子：

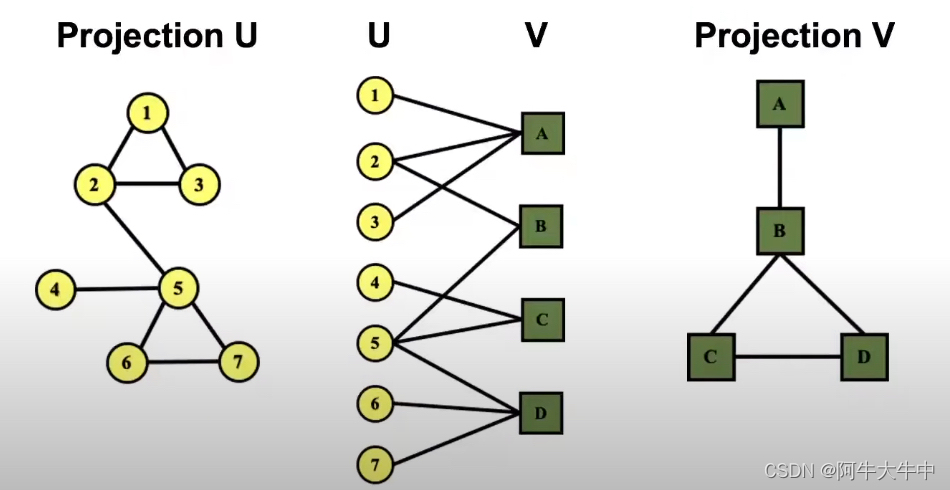
如果我们有一个二部图（中间），我们就可以把它投影到左侧或者右侧，当把它投射出来的时候，在投影图中我只使用一侧的节点。连接节点的方式是，将在一对节点之间创建一个连接，如果他们至少有一个共同的邻居。

所以如果这些是作者，将创建一个合作或共同作者图表，如果两位作者共同撰写了至少一篇论文，那么将他们联系起来。

举个例子1，2，3这篇论文（A）的三位合著者，所以它们都是相互连接的。例如，3号和4号没有共同撰写论文，

所以它们之间没有联系。举个例子，5号和2号共同撰写了一篇论文，所以他们之间有联系，因为他们是合著者。

类似的右边也可以做出论文关系图。

3.2 图的表示

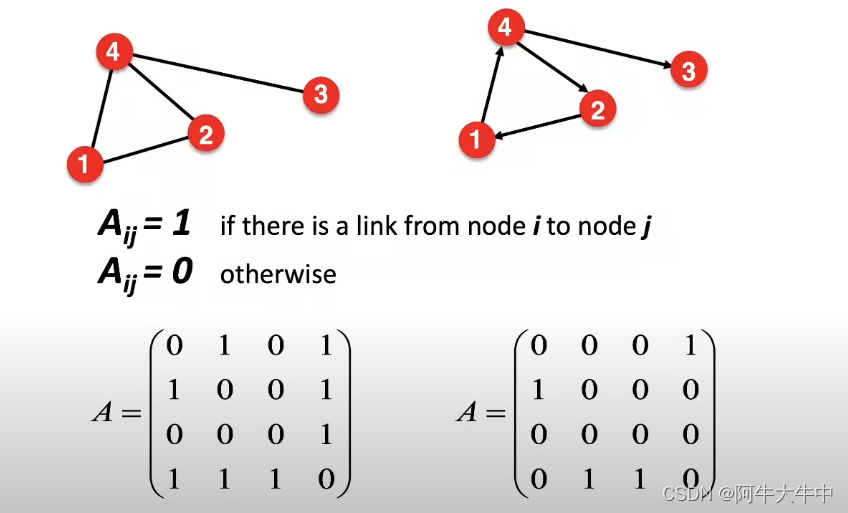
可以用邻接矩阵表示图结构。但也有一些问题。

真实世界的网络结构往往比较稀疏：

就会导致我们创建的邻接矩阵存在大量0元素。

还有其他两种常见的图表示方法：

• 边列表（edge list）：

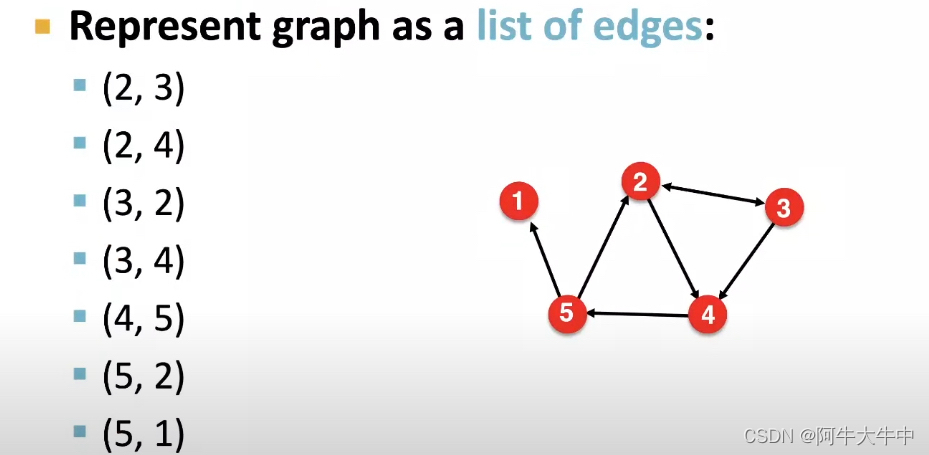
这种表示法的问题在于，很难对图进行任何形式的操作或分析，因为即使计算给定节点的度数也不是平凡的（计算给定节点的度数的复杂度比较高）。

• 邻接列表（Adjacency list）：

4. 节点和边的属性

节点、边、整个图可以有附加的属性。例如，一条边可以有一个权值。

课程中还讲了一些数据结构中的图的概念（连通图、强连通图…），这里就不赘述了。