高等数学教材重难点题型总结（六）定积分的应用

本章全是物理题，总的来说计算层面并不难，难点主要在于：对于体积和面积的题，核心在于抽象出面积/体积元素——本质上就是被积函数；对于物理题，基础的物理的公式一定要牢记~
 

1.求平面面积

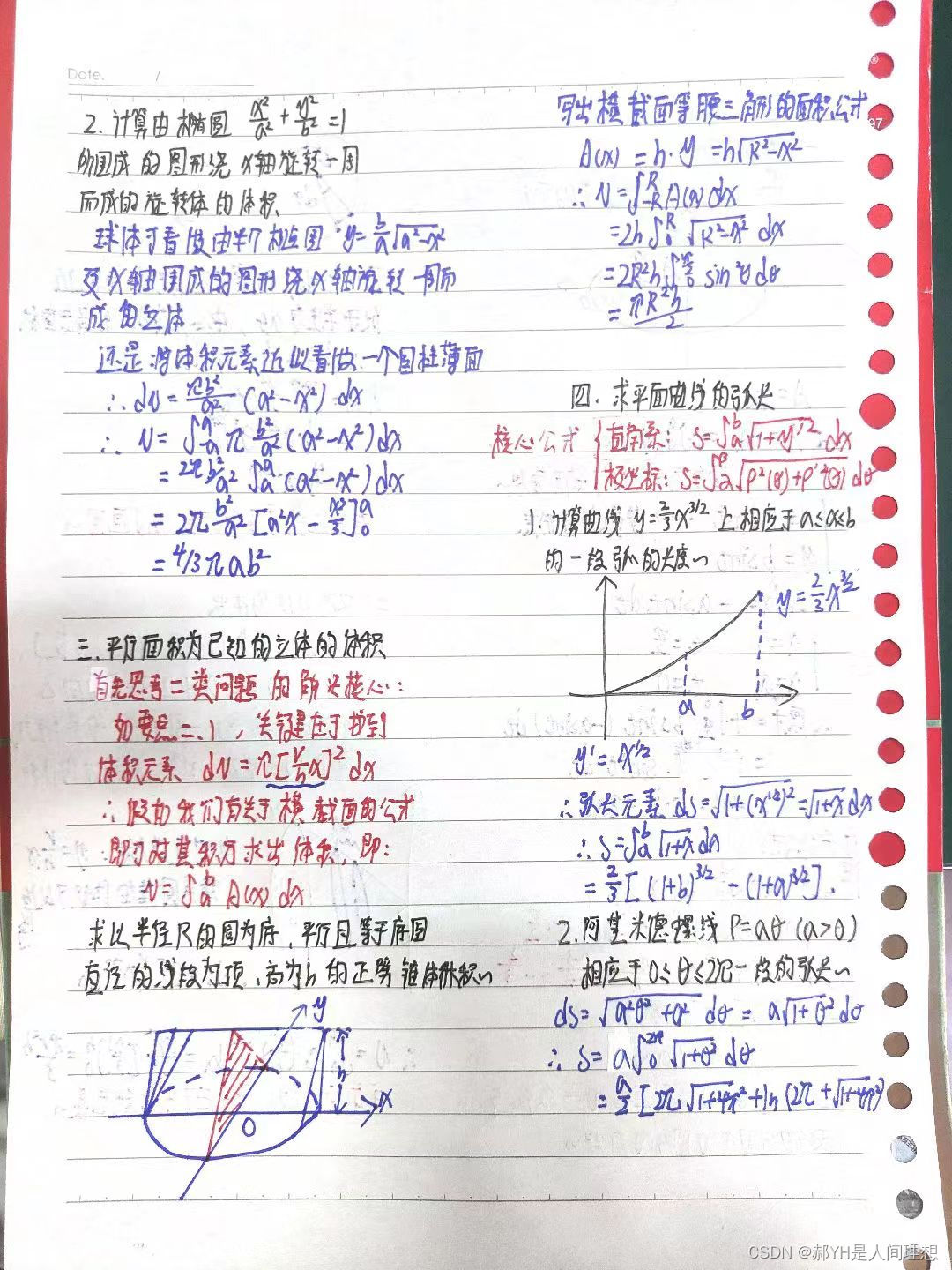
2.求旋转体的体积

3.平行面积为已知的立体的 体积

4.求平面曲线的弧长

5.定积分在物理学上的应用

 考研数学一大纲中对这一章的要求：

        掌握用定积分表达和计算一些几何量与物理量(平面图形的面积、平面曲线的弧长、旋转体的体积及侧面积、平行截面面积为已知的立体体积、功、引力、压力、质心、形心等)及函数的平均值.

目录

6.1定积分的元素法

6.2定积分应用于求面积

6.3定积分应用于求体积

6.4定积分求平面曲线的弧长 

---

6.1定积分的元素法

• 定积分适合解决不规则累积求和问题，是“分割，近似，求和，取极限(极限存在)”四步运算压缩成一步新的运算，叫做定积分。
• 有了定积分的概念之后，再求曲边梯形面积的话，直接就是 ∫abf(x)dx 就好了。也就是说只要能正确地列出 ∫abf(x)dx 这个式子(再计算定积分)问题就解决了。
• 那么，怎么正确地列出 ∫abf(x)dx 呢？它表示的是曲边梯形的面积，这个面积可以从 x 轴方向，切成微小的细条，再累积出来~

        又叫做微元法，所谓的“微”即微分，将难以计算面积的物块分为无数个小面积；而积分的作用就是将这些无数个微小的元素累加，以此计算面积等答案~

元素法的一般步骤：

• ①根据问题的具体情况，选取一个变量x为积分变量，并确定它的变化区间[a,b]
• ②把区间[a,b]分割为n个小区间，取其中任意一个小区间，求出相应的目标值（面积/体积/弧长等等）。如果这个目标值能近似地表示为[a,b]上的一个连续函数在变量x处的值f(x)与dx的乘积，就把f(x)dx称为U的元素，记作dU，即dU=f(x)dx
• ③将区间[a,b]上所有的U的元素都累加起来求极限。也就是将所求量U的元素f(x)dx作为被积表达式，在区间[a,b]上做定积分。

主要的思想就是 分割，取近似值，求和，取极限

定积分的几何意义：其绝对值表示曲线梯形的面积

• 第一步，确定所求量是对谁累积，从哪累积到哪，即：确定积分变量 x 及其范围 [a,b]
• 第二步，任取一小段 [x,x+dx] ，（借助图形）得到部分量（微元）的计算式： dA=f(x)dx
• 第三步，累积得到总量（所求量）： A=∫abdA=∫abf(x)dx

        该过程就是定积分元素法，也叫定积分微元法，它适合所有不规则累积求和问题。

        再精炼叙述一下，也是定积分元素法的解题步骤：

1. 确定积分变量及其范围 x∈[a,b]
2. 任取一小段 [x,x+dx] ，（借助图形）得到（近似）微元的计算式： dA=f(x)dx
3. 累积得到总量：

        A=∫abdA=∫abf(x)dx

6.2定积分应用于求面积

• 利用直角坐标系求解面积，有X型积分和Y型积分两种，重点是规划正确的上下限~
• 还可以利用极坐标求面积

6.3定积分应用于求体积

• 旋转体：某曲线绕某轴旋转后形成的物体~
• 所有公式的原理：对曲线求积分相当于加维度变为求面积，对面积求积分相当于添加高度求体积~

6.4定积分求平面曲线的弧长 

        对于用参数方程表示的平面曲线，有如下公式，参数方程就是个好的思维方式，如果要计算三维空间里的曲线弧长，是不是也很容易推广，如果三维空间里曲线，用直角坐标方程表示，那曲线弧长计算公式的推导就更绕了。

        这个参数方程，形式上 对 x,y 是对称的， 推导出的曲线弧长计算公式，对x 和 y 也是对称的。更容易理解和记忆。 对于 参数t 的一个 微小变化 dt, 在x 轴方向上的 坐标变化， 可以用 dt 乘以，x的参数方程的在这一点的导数值来逼近。 只要dt 足够小，差别就是高阶无穷小。 对 y 轴方向上的坐标变化， 也是类似。 再用勾股定理，计算出斜边长度，再积分，就是上边这个公式了。