-
【优选算法精品】前缀和
一、前缀和
前缀和问题
前缀和用来快速解决某一段连续区间的和。
时间复杂度O(1)
注意:不要背模板,不要背模板,不要背模板!!!
一维前缀和模板
重点:不要背模板,不要背模板,不要背模板!!!
每道题的情况不同,唯一相同的是前缀和思想,利用这个思想求一段连续区间内所有元素的和即可。
二维前缀和模板
以该题为例:
利用二维前缀和数组的思想:
dp[i][j]表示:从[1,1]坐标开始到[i,j]坐标结束,这段连续区间内所有元素的和。dp[i][j] = dp[i-1][j] + dp[i][j-1] + arr[i][j] - dp[i-1][j-1]- 1
细节处理
由于i应该要从1开始,所以当i = 0时,会越界,这里可以多开一个空间,并保证空间的初始化不会影响后续的结果。
题目1
思路
使用一维前缀和的思想,假设
[0~i-1]区间的所有元素的和 = f[i];
[i+1,n-1]区间的所有元素的和 = g[i];f[i] = f[i-1] + arr[i-1];
g[i] = g[i+1] + arr[i+1];细节处理:
- f[0] = 0,g[n-1] = 0
因为这种边界情况会越界
f从左到右开始求和
g从右到左求和
题目2
思路
与题目一思路几乎一样。

题目3
这道题上强度了,难度比较大,我是看了解析看了三遍才弄懂它的思路。

题目4
这道题的整体思路与上一道题的思路也是几乎相同。
主要区别就是这道题要引入一个数学定理。
还有一个在c++和java两个语言中,负%正=负;这个问题在本道题中需要进行修正。
其他细节问题一样的。
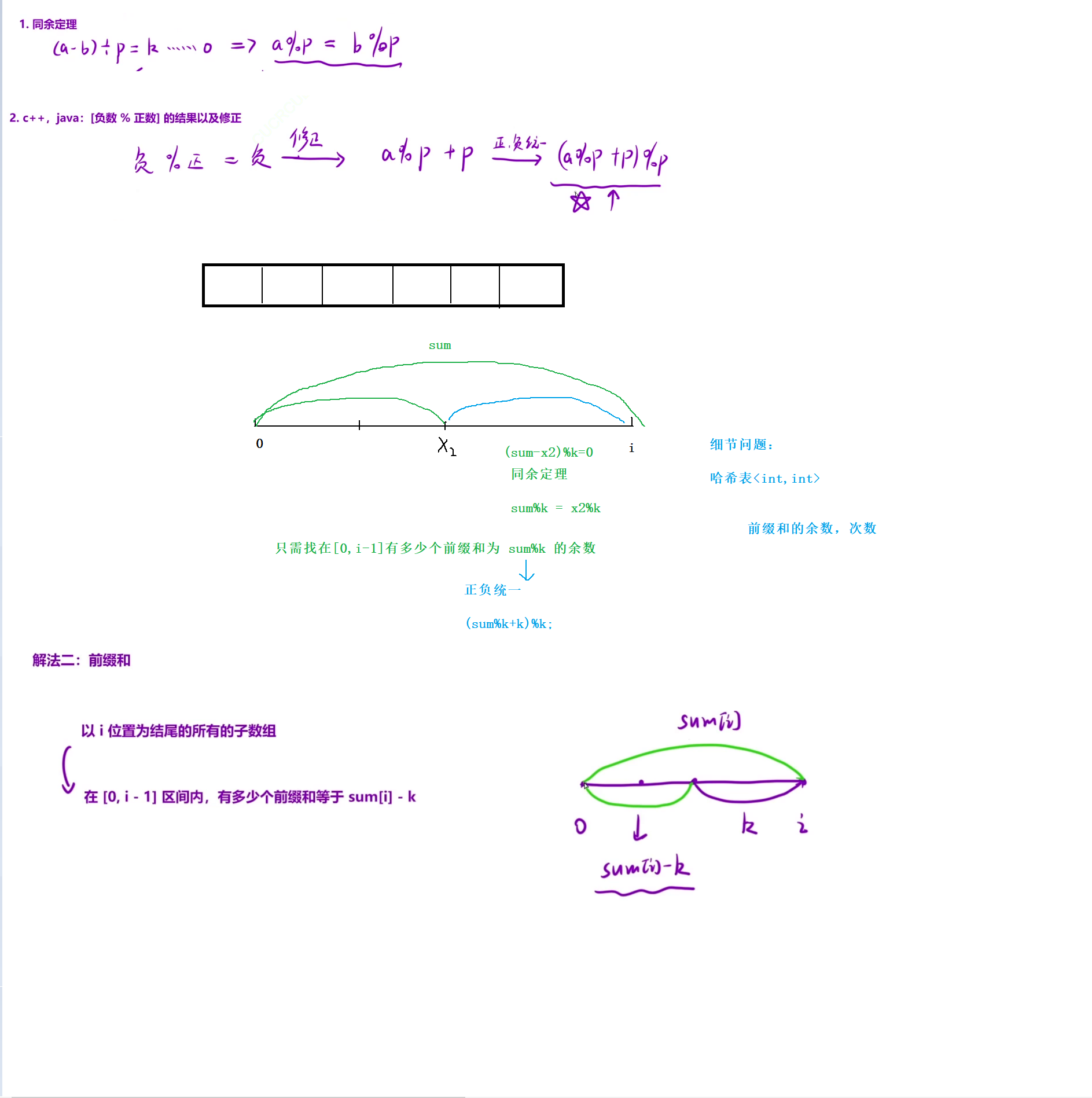
题目5
解题思路:
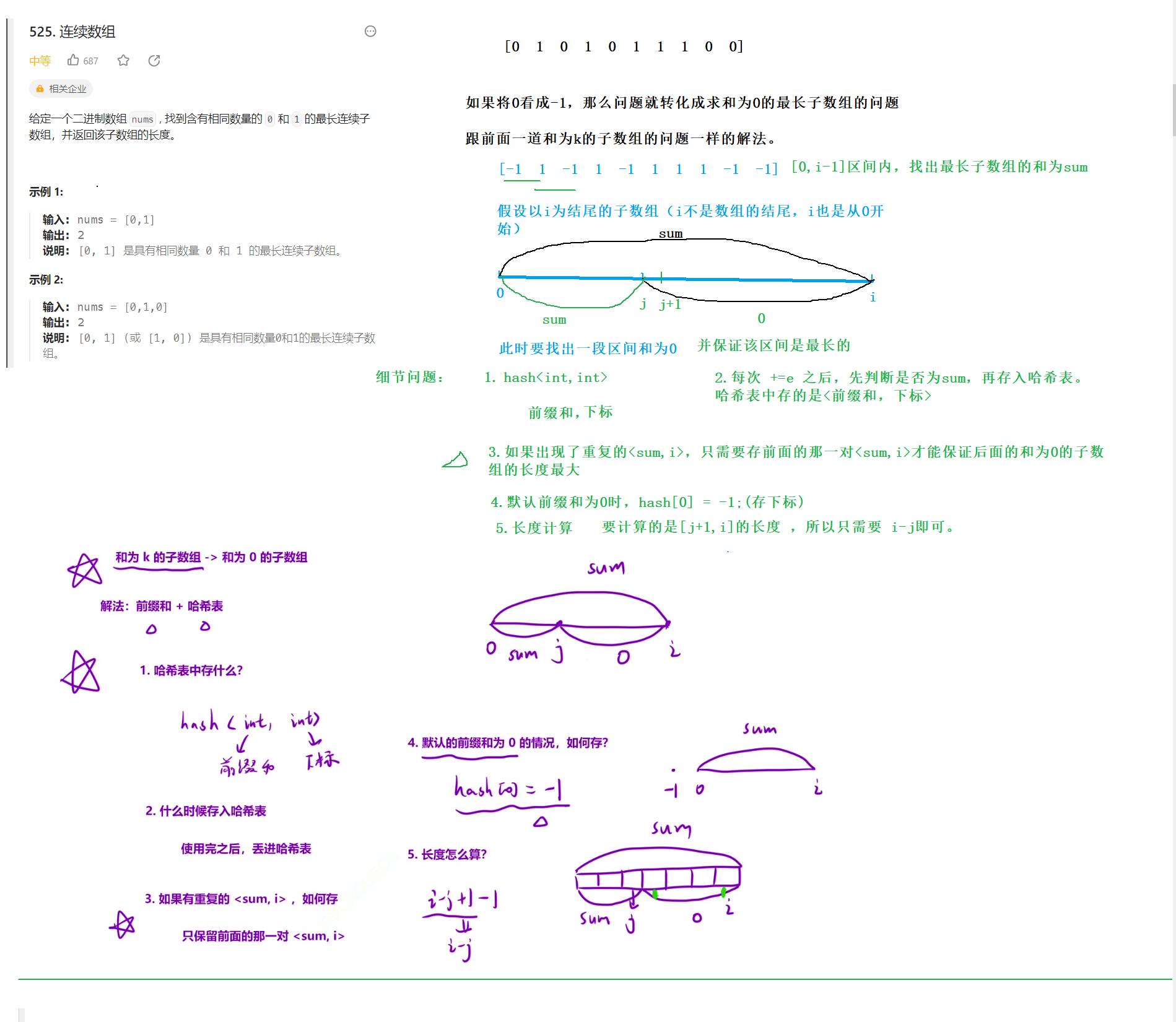
题目6
这道题是一个二维前缀和,难度还是挺大的,不过只要把思路捋清楚,多花点时间也是可以的。

总结
这篇文章是关于前缀和的题目解题思路以及一些模板,还是那句话,不要背模板。
-
相关阅读:
同步协程的必备工具: WaitGroup
VS2019+QT5.12.9环境下,调试QString无显示解决
虚拟机和开发板互Ping问题
SAP MM学习笔记27- 购买依赖(采购申请)
ElementUI浅尝辄止28:Dropdown 下拉菜单
解决Python调试OSError: [WinError 193] %1 不是有效的 Win32 应用程序
win10如何清除ftp自动保存的账户密码
UE5场景逐渐变亮问题
用ARM进行汇编语言编程(3)逻辑移位和轮换,条件与分支
《代码大全2》第17章 不常见的控制结构
- 原文地址:https://blog.csdn.net/w2915w/article/details/134056497