查找算法-斐波那契查找法（Fibonacci Search）

目录

  查找算法-斐波那契查找法（Fibonacci Search）

1、说明

2、算法分析

3、C++代码 

---

  查找算法-斐波那契查找法（Fibonacci Search）

1、说明

斐波那契查找法又称为斐氏查找法，此查找法和二分法一样都是以分割范围来进行查找的，不同的是斐波那契查找法不是按对半方式来分割的，而是以斐波那契级数的方式来分割的。

斐波那契级数的定义如下：

        

        

斐波那契级数：0、1、1、2、3、5、8、13、21、34、55、89、...。也就是除了第0个和第1个元素外，级数中的每个元素值都是前两个元素值的和。

斐波那契查找法的好处是只需要用到加减运算而不需要用到乘除运算，这从计算机运算的过程来看效率会高于前两种查找法。在尚未介绍斐波那契查找法之前，我们先来认识斐波那契树。所谓斐波那契树，是以斐波那契级数的特性来建立的二叉树，其建立的原则如下：

1. 斐波那契树的左右子树均为斐波那契树。
2. 当数据个数确定时，若想确定斐波那契树的层数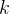值是多少，我们必须找到一个最小的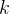值，使得斐波那契层数的。
3. 斐波那契树的树根一定是一个斐波那契树，且子节点与父节点差值的绝对值为斐波那契数。
4. 当时，斐波那契树的树根为，左子树为层斐波那契树（其树根为），右子树为层斐波那契树（其树根为）。
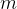5. 若值不是斐波那契树的值，则可以找出一个，使得，，再按斐波那契树的建立原则完成斐波那契树的建立，最后斐波那契树的各节点再减去差值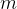即可，并把小于1的节点去掉。

2、算法分析

1. 斐波那契查找法的平均比较次数少于二分查找法，但在最坏的情况下二分查找法较快，其平均时间复杂度为。
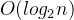2. 斐波那契查找法较为复杂，需额外产生斐波那契树。

3、C++代码 

#include
using namespace std;
 
void SetData(int* Data, int Size) {
	for (int i = 0; i < Size; i++) {
		Data[i] = rand() % 150 + 1;
	}
}
 
void Sort(int* Data, int Size) {
	for (int i = 0; i < Size; i++) {
		for (int j = i + 1; j < Size; j++) {
			if (Data[i] > Data[j]) {
				int temp = Data[i];
				Data[i] = Data[j];
				Data[j] = temp;
			}
		}
	}
}
 
void Print(int* Data, int Size) {
	for (int i = 0; i < Size ; i++) {
		cout << Data[i] << "  ";
	}
	cout << endl;
}
 
int* Fibonacci(int Size) {
	int* fib = new int[Size];
	fib[0] = 0;
	fib[1] = 1;
	for (int i = 2; i < Size; i++) {
		fib[i] = fib[i - 1] + fib[i - 2];
	}
	return fib;
}
 
int FibonacciSearch(int* Data, int Size, int Value) {
	int low = 0;
	int high = Size - 1;
	int k = 0;
	int mid = 0;
 
	int* fib = Fibonacci(Size);
 
	while (high > fib[k] - 1) {
		k++;
	}
	int* temp = new int[fib[k]];
	for (int i = 0; i < Size; i++) {
		temp[i] = Data[i];
	}
	for (int i = Size; i < fib[k]; i++) {
		temp[i] = Data[high];
	}
 
	while (low <= high) {
		mid = low + fib[k - 1] - 1;
		if (Value < temp[mid]) {
			high = mid - 1;
			k--;
		}
		else if (Value > temp[mid]) {
			low = mid + 1;
			k -= 2;
		}
		else
			return mid <= high ? mid : high;
	}
	return -1;
}
 
int main() {
	int Size = 20;
	int* Data = new int[Size] {0};
 
	SetData(Data, Size);
	Sort(Data, Size);
	cout << "原始数据：" << endl;
	Print(Data, Size);
	cout << "---------------------" << endl;
 
	int num = 0;
	cout << "请输入想要查找的数据：";
	cin >> num;
 
	int index = -1;
	index = FibonacciSearch(Data, Size, num);
 
	if (index != -1)
		cout << "查找的数据在数据库的第[ " << index + 1 << " ]位" << endl;
	else
		cout << "在数据库中没有找到该数据" << endl;
 
	return 0;
}

输出结果