四个小车相对导航集中式无迹卡尔曼滤波（fullyCN-EKF）

背景

二维情况下，四个小车各自有绝对定位（GNSS），相互之间部分有相对定位（UWB）时，一个滤波器搞定四个小车的状态滤波。使用EKF。

建模

四个小车，每个有x、y两个轴，所以状态量有4*2=8维，观测量为各自的GNSS绝对定位+相对定位（1对2+2对1+2对3+3对3+4对3），所以观测量Z的维度为（4+5）*2=18维。
定义系统误差矩阵Q和观测误差协方差矩阵R为：

Q = 0.1*diag(ones(8,1))
R = 0.1*diag([ones(18,1)])
1
2

定义四个小车的初值为：（1,0）、（2,0）、（3,0）、（4,0），各自的状态方程设置简单一点，统一为：
X ˙ k + 1 = f ( X k ) + u ( k ) = X k + ( cos ⁡ ( 0.1 k ) cos ⁡ ( 0.1 k ) + 1 ) ) \dot{X}_{k+1}=f(X_{k})+u(k)=X_{k}+\left.\left(cos(0.1k)cos(0.1k)+1)

\right.\right) X˙k+1​=f(Xk​)+u(k)=Xk​+(cos(0.1k)cos(0.1k)+1)​)
因此四个小车混在一起，可以得到状态量：
$${\mathbf{x}}_k={\left[{\left({\mathbf{x}}_k^1\right)}^{\mathrm{T}},{\left({\mathbf{x}}_k^2\right)}^{\mathrm{T}},\dots ,{\left({\mathbf{x}}_k^4\right)}^{\mathrm{T}}\right]}^{\mathrm{T}}$$
X对应的状态变换矩阵为8维的主对角矩阵：

F = eye(8);
1

观测数据生成:

Q_abs = 0.2*diag([1,1]);w_abs=sqrt(Q_abs)*randn(size(Q_abs,1),length(t));Zflight.a = flight.a+w_abs; %生成飞机a的绝对观测量
Q_abs = 0.2*diag([1,1]);w_abs=sqrt(Q_abs)*randn(size(Q_abs,1),length(t));Zflight.b = flight.b+w_abs;
Q_abs = 0.2*diag([1,1]);w_abs=sqrt(Q_abs)*randn(size(Q_abs,1),length(t));Zflight.c = flight.c+w_abs;
Q_abs = 0.2*diag([1,1]);w_abs=sqrt(Q_abs)*randn(size(Q_abs,1),length(t));Zflight.d = flight.d+w_abs;
Q_coo = 0.1*diag([1,1]);w_coo=sqrt(Q_coo)*randn(size(Q_coo,1),length(t));Zflight.ab = flight.a-flight.b+w_coo; %生成a-b的相对观测量
Q_coo = 0.1*diag([1,1]);w_coo=sqrt(Q_coo)*randn(size(Q_coo,1),length(t));Zflight.ac = flight.a-flight.c+w_coo;
Q_coo = 0.1*diag([1,1]);w_coo=sqrt(Q_coo)*randn(size(Q_coo,1),length(t));Zflight.ad = flight.a-flight.d+w_coo;
Q_coo = 0.1*diag([1,1]);w_coo=sqrt(Q_coo)*randn(size(Q_coo,1),length(t));Zflight.ba = flight.b-flight.a+w_coo;
Q_coo = 0.1*diag([1,1]);w_coo=sqrt(Q_coo)*randn(size(Q_coo,1),length(t));Zflight.bc = flight.b-flight.c+w_coo;
Q_coo = 0.1*diag([1,1]);w_coo=sqrt(Q_coo)*randn(size(Q_coo,1),length(t));Zflight.bd = flight.b-flight.d+w_coo;
Q_coo = 0.1*diag([1,1]);w_coo=sqrt(Q_coo)*randn(size(Q_coo,1),length(t));Zflight.ca = flight.c-flight.a+w_coo;
Q_coo = 0.1*diag([1,1]);w_coo=sqrt(Q_coo)*randn(size(Q_coo,1),length(t));Zflight.cb = flight.c-flight.b+w_coo;
Q_coo = 0.1*diag([1,1]);w_coo=sqrt(Q_coo)*randn(size(Q_coo,1),length(t));Zflight.cd = flight.c-flight.d+w_coo;
Q_coo = 0.1*diag([1,1]);w_coo=sqrt(Q_coo)*randn(size(Q_coo,1),length(t));Zflight.da = flight.d-flight.a+w_coo;
Q_coo = 0.1*diag([1,1]);w_coo=sqrt(Q_coo)*randn(size(Q_coo,1),length(t));Zflight.db = flight.d-flight.b+w_coo;
Q_coo = 0.1*diag([1,1]);w_coo=sqrt(Q_coo)*randn(size(Q_coo,1),length(t));Zflight.dc = flight.d-flight.c+w_coo;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

再定义观测方程：

Z_hat =[Xpre(1);Xpre(2);Xpre(3);Xpre(4);Xpre(5);Xpre(6);Xpre(7);Xpre(8);
    Xpre(1*2-1)-Xpre(2*2-1);Xpre(1*2)-Xpre(2*2); %Zab
    Xpre(2*2-1)-Xpre(1*2-1);Xpre(2*2)-Xpre(1*2); %Zba
    Xpre(2*2-1)-Xpre(2*3-1);Xpre(2*2)-Xpre(2*3); %Zbc
    Xpre(2*3-1)-Xpre(2*2-1);Xpre(2*3)-Xpre(2*2);%Zcb
    Xpre(2*4-1)-Xpre(2*3-1);Xpre(2*4)-Xpre(2*3)%Zdc
    ];
1
2
3
4
5
6
7

上述代码第一行代表四个小车的绝对观测量（每个小车2个维度，所以共8维）。
第二行表示第一个的坐标减去第二个的坐标（2→1的观测量），第三行至第六行以此类推。
由Z可以得到观测矩阵：

H = [1,0,0,0,0,0,0,0;
        0,1,0,0,0,0,0,0;
        0,0,1,0,0,0,0,0;
        0,0,0,1,0,0,0,0;
        0,0,0,0,1,0,0,0;
        0,0,0,0,0,1,0,0;
        0,0,0,0,0,0,1,0;
        0,0,0,0,0,0,0,1;
        1,0,-1,0,0,0,0,0;
        0,1,0,-1,0,0,0,0;
        -1,0,1,0,0,0,0,0;
        0,-1,0,1,0,0,0,0;
        0,0,1,0,-1,0,0,0;
        0,0,0,1,0,-1,0,0;
        0,0,-1,0,1,0,0,0;
        0,0,0,-1,0,1,0,0;
        0,0,0,0,-1,0,1,0;
        0,0,0,0,0,-1,0,1];
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

滤波

PP=F*P*F'+Q;
Kk=PP*H'/(H*PP*H'+R);
flight_ekf.fully(:,k)=Xpre+Kk*(flightZ.fully(:,k)-Z_hat);
P=PP-Kk*H*PP;
flightP_num.fully(k,:,:) = P;
1
2
3
4
5

绘图

a机的x轴与y轴位移：

a机的x轴与y轴误差曲线图：

a机x轴和y轴的累积误差概率曲线图：

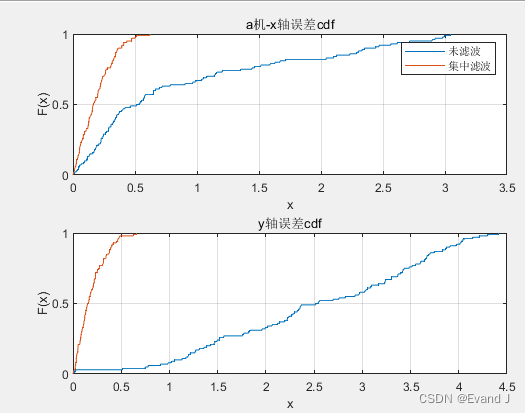
b机x轴和y轴的累积误差概率曲线图：

c机x轴和y轴的累积误差概率曲线图：

d机x轴和y轴的累积误差概率曲线图：

完整程序下载链接：
https://download.csdn.net/download/callmeup/88471122
有疑问留言or联系电子邮箱：evandworld@foxmail.com，看到了一一般都会回复