LeetCode977——有序数组的平方

LeetCode977——有序数组的平方

给你一个按 非递减顺序 排序的整数数组 nums，返回 每个数字的平方 组成的新数组，要求新数组也按 非递减顺序 排序。

输入：nums = [-4,-1,0,3,10]
输出：[0,1,9,16,100]
解释：平方后，数组变为 [16,1,0,9,100]
排序后，数组变为 [0,1,9,16,100]

输入：nums = [-7,-3,2,3,11]
输出：[4,9,9,49,121]

1.暴力解

首先对原来的数组进行求平方操作，再选用一种排序算法对平方后的数组进行排序。

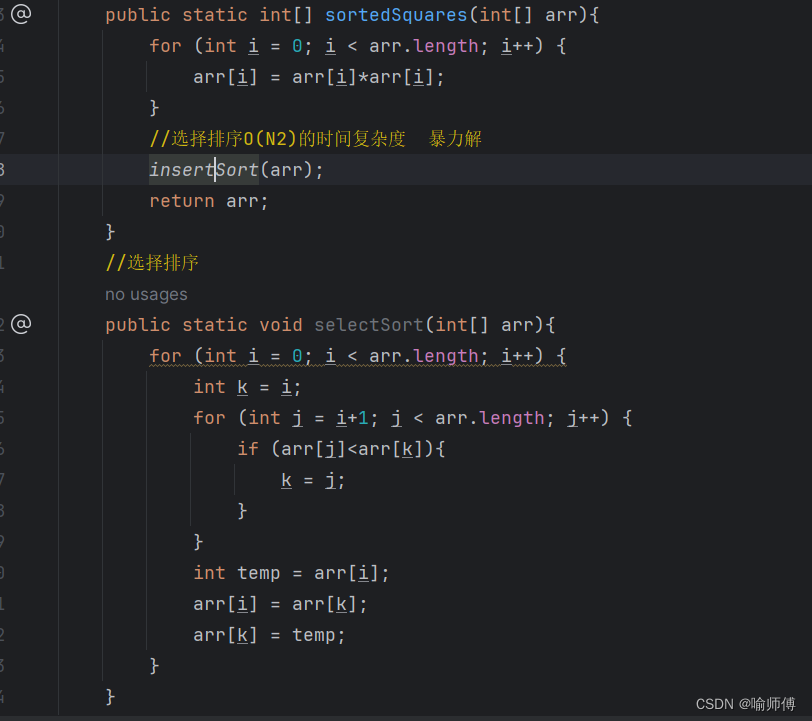
空间复杂度为O(1),时间复杂度取决于你采用的排序算法。

 public static int[] sortedSquares(int[] arr){
        for (int i = 0; i < arr.length; i++) {
            arr[i] = arr[i]*arr[i];
        }
        //选择排序O(N2)的时间复杂度  暴力解
        insertSort(arr);
        return arr;
    }
    //选择排序
    public static void selectSort(int[] arr){
        for (int i = 0; i < arr.length; i++) {
            int k = i;
            for (int j = i+1; j < arr.length; j++) {
                if (arr[j]<arr[k]){
                    k = j;
                }
            }
            int temp = arr[i];
            arr[i] = arr[k];
            arr[k] = temp;
        }
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

2.双指针法

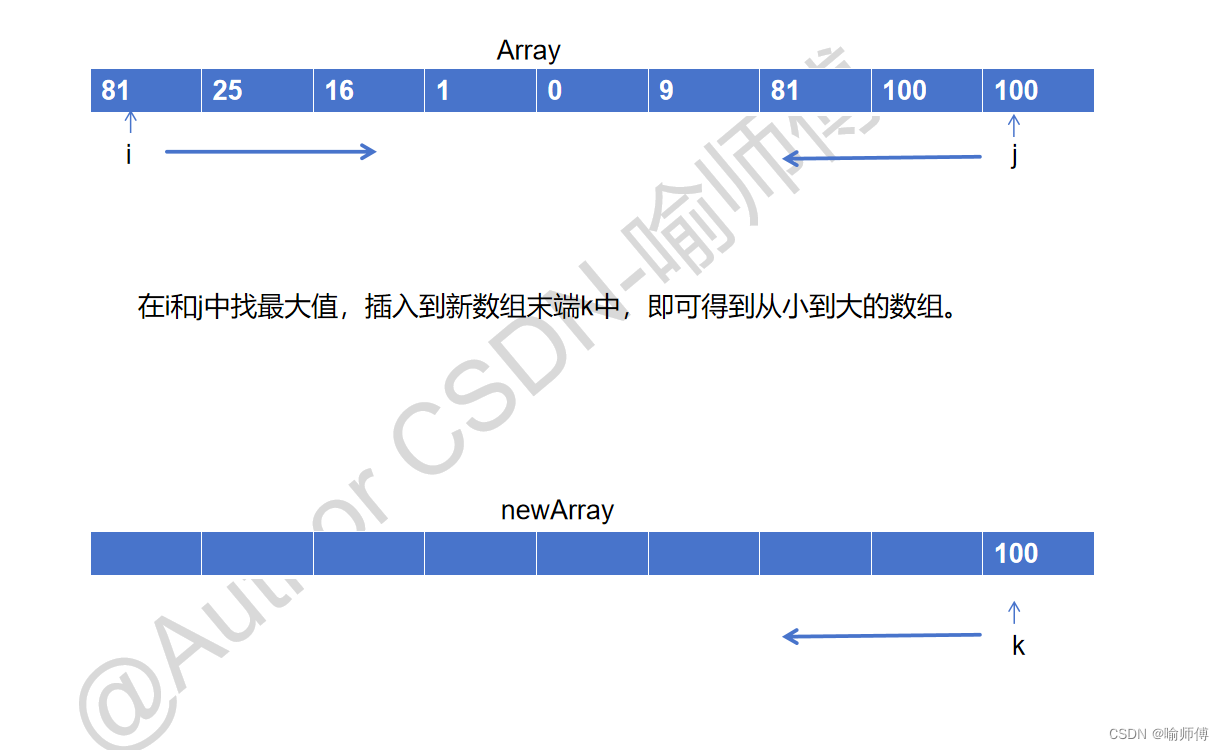
在平方后的数组首尾分别放置指针，因为数组可能会存在负数且数组 非递减顺序 ，所以平方后的最大值必定在首尾中选取。

如果i的值大于j，将i存入新数组的最后一位并执行 i++ k–，如果j的值大于i，将j存入新数组的最后一位并执行j-- k–，这样下来 newArr便为有序的了。

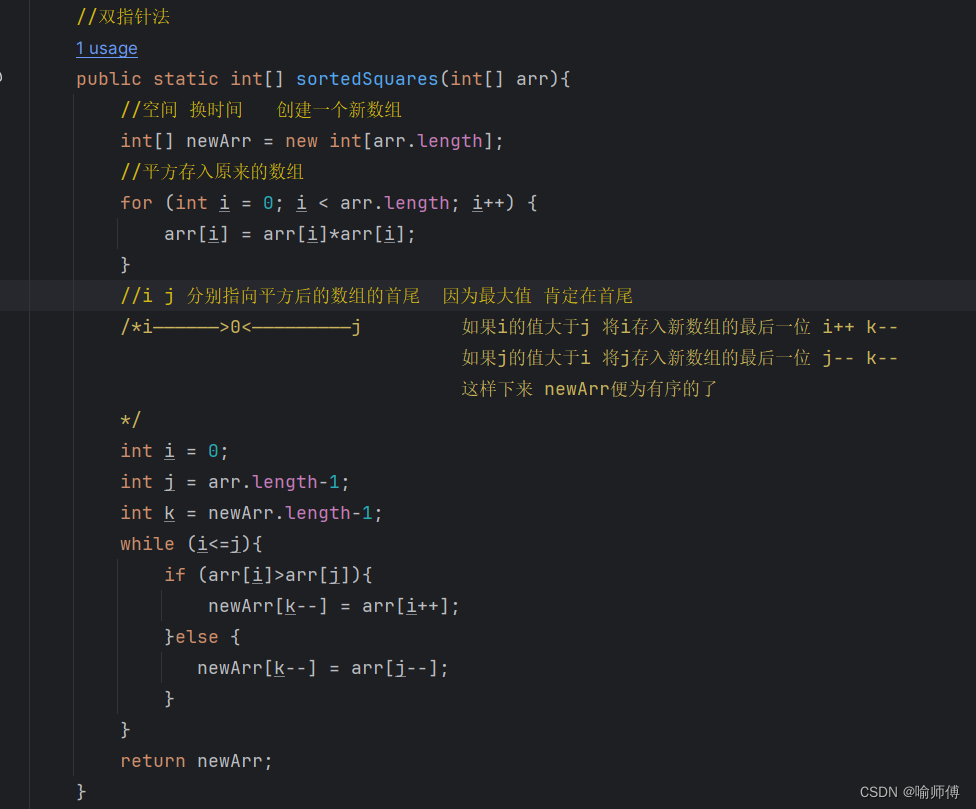
时间复杂度为O(N)，空间复杂度为O(N)，相对于暴力解法，时间复杂度更低，以空间换时间。

public static int[] sortedSquares(int[] arr){
        //空间 换时间   创建一个新数组
        int[] newArr = new int[arr.length];
        //平方存入原来的数组
        for (int i = 0; i < arr.length; i++) {
            arr[i] = arr[i]*arr[i];
        }
        //i j 分别指向平方后的数组的首尾  因为最大值 肯定在首尾
        /*i——————>0<—————————j         如果i的值大于j 将i存入新数组的最后一位 i++ k--
                                       如果j的值大于i 将j存入新数组的最后一位 j-- k--
                                       这样下来 newArr便为有序的了
        */
        int i = 0;
        int j = arr.length-1;
        int k = newArr.length-1;
        while (i<=j){
            if (arr[i]>arr[j]){
                newArr[k--] = arr[i++];
            }else {
               newArr[k--] = arr[j--];
            }
        }
        return newArr;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

Tips：双指针的思想还是很重要的，有兴趣的小伙伴可以去LeetCode27看一下，巩固一下双指针的思想。

仅供学习使用！