二叉搜索树

目录

一、概念

二、插入数据

三、查找数据

四、删除数据

---

一、概念

二叉搜索树：又称为二叉排序树，它或是一棵空树，或是一棵具有以下性质的二叉树：

（1）若它的左子树不为空，则左子树上的所有节点的值都小于根节点的值

（2）若它的右子树不为空，则右子树上的所有节点的值都大于根节点的值

（3）它的左右子树也分别是二叉搜索树

例如：

图中二叉搜索树中序遍历的结果：3 5 7 10 11 12 40  

由于二叉搜索树的性质，二叉搜索树中序遍历的结果是升序

二、插入数据

若二叉搜索树为空树，则直接将节点放在根节点位置处。

若二叉搜索树不为空树，由二叉树的性质（左子树上的所有节点的值都小于根节点的值，右子树上的所有节点的值都大于根节点的值），可通过比较插入节点和当前节点cur的值，找到插入节点的位置

 

 找到插入节点的位置后，要通过cur的父亲节点将插入节点连接起来，因此我们可以定义一个parent节点，指向cur的父亲节点，来帮助我们插入节点

若插入的值与二叉搜索树中节点的值相同，则插入失败，返回false

代码实现：

public class BinarySearchTree {
    static class Node{
        private int val;
        private Node left;
        private Node right;
        public Node(int val){
            this.val = val;
        }
 
    }
    //创建根节点
    public Node root;
    //插入数据
    public boolean insert(int val){
        Node node = new Node(val);
        //根节点为空，直接将数据放在根节点位置
        if(root == null){
            root = node;
            return true;
        }
        //不为根节点，查找插入位置
        Node cur = root;
        Node parent = null;
        while(cur != null){
            if(node.val < cur.val){
                parent = cur;
                cur = cur.left;
            }else if(node.val > cur.val){
                parent = cur;
                cur = cur.right;
            }else {//若相等，则插入失败
                return false;
            }
        }
        if(parent.val > node.val){
            parent.left = node;
        }else{
            parent.right = node;
        }
        return true;
    }
}

三、查找数据

将待查找数据data与节点的值进行比较，若相同，则返回；若data小于节点的值，则向左子树继续查找；若data大于节点的值，则向右子树继续查找

代码实现：

public boolean search(int data){
    if(root == null){//若根节点为null，无数据，直接返回false
        return false;
    }
    Node cur = root;
    while(cur != null){
        if(data == cur.val){
            return true;
        }else if(data < cur.val){
            cur = cur.left;
        }else{
            cur = cur.right;
        }
    }
    return false;
}

四、删除数据

当删除二叉搜索树中节点时，需分情况删除

待删除节点为cur，其父亲节点为parent

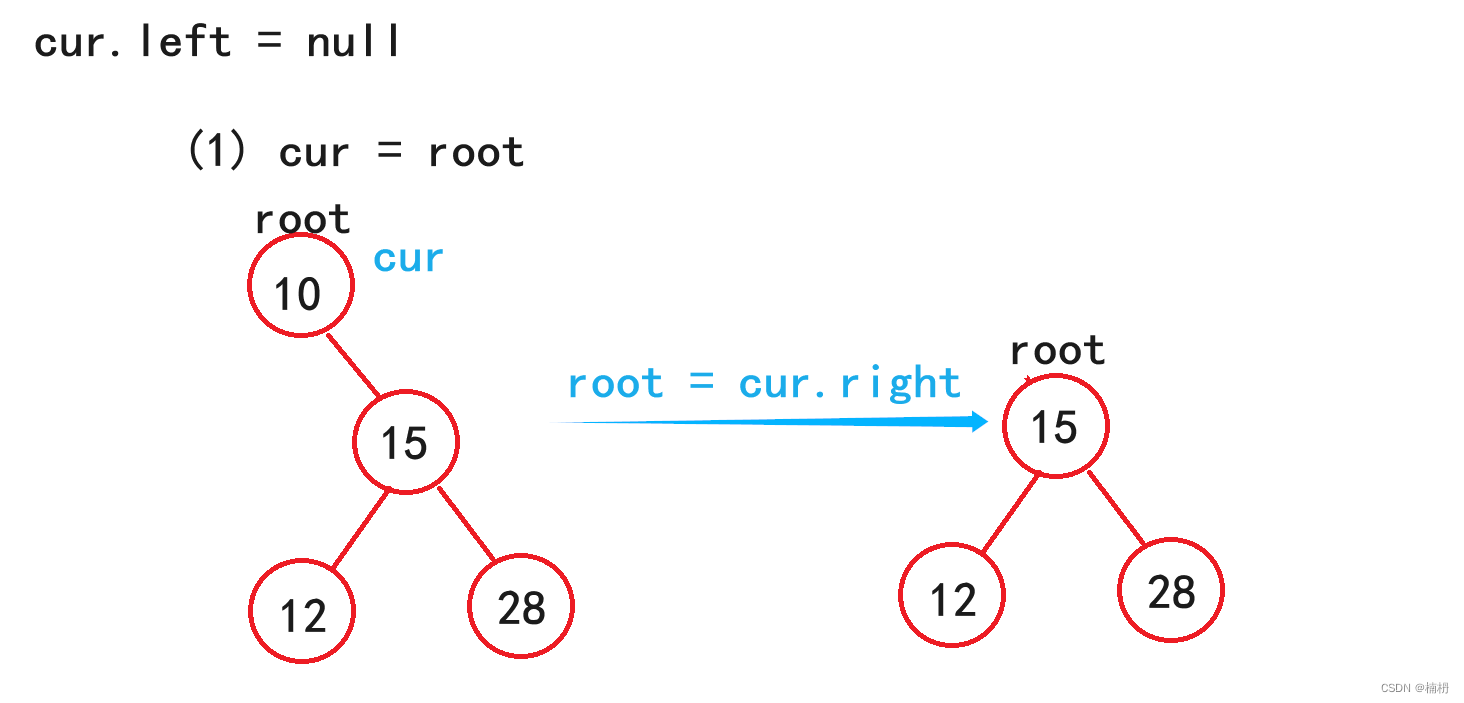
1. cur.left = null

（1）若cur = root，则root = cur.right

（2）若cur != root 且 cur = parent.left ，则parent.left = cur.right

（3）若cur != root 且 cur = parent.right，则parent.right = cur.right

2. cur.right = null

（1）cur = root，则 root = cur.right

（2）cur != root 且 cur = parent.left，则parent.left = cur.left

（3）cur != root 且 cur = parent.right，则parent.right = cur.left

3. cur.left != null 且 cur.right != null

此时通过替换进行删除

由于cur中的数据比左子树大，比右子树小，因此我们可以在左子树中寻找最大的数据（即左子树中最右边的数据），或是在右子树寻找最小的数据（即右子树中最左的数据），用找到的值替换掉cur，再删除找到的值

由于替换的值为右子树最左的节点（或左子树最右的节点），此时删除的情况变为 2 中的（2）或（3）（或是 1 中的（2）或（3）），便于删除

代码实现：

public boolean remove(int key){
    Node cur = root;
    Node parent = null;
    while(cur != null){
        //找到需删除节点
        if(cur.val < key){
            parent = cur;
            cur = cur.right;
        }else if(cur.val > key){
            parent = cur;
            cur = cur.left;
        }else {//找到了，开始删除
            removeNode(cur,parent);
            return true;
        }
    }
    //未找到，删除失败
    return false;
}
private void removeNode(Node cur, Node parent){
    if(cur.left == null){
        if(cur == root){
            root = cur.right;
        }else if(parent.left == cur){
            parent.left = cur.right;
        }else{
            parent.right = cur.right;
        }
    }else if(cur.right == null){
        if(cur == root){
            root = cur.left;
        }else if(parent.left == cur){
            parent.left = cur.left;
        }else{
            parent.right = cur.left;
        }
    }else {
        Node targetParent = cur;
        Node target = cur.right;
        //在cur的右子树查找最小值
        while(target.left != null){
            targetParent = target;
            target = target.left;
        }
        //将cur的值替换为target的值
        cur.val = target.val;
        if(targetParent.left == target){
            targetParent.left = target.right;
        }else {
            targetParent.right = target.right;
        }
    }
}