• 【C++代码】回溯，子集，组合，全排列，去重--代码随想录

    题目：分割回文串

    • 给你一个字符串 s，请你将 s 分割成一些子串，使每个子串都是 回文串 。返回 s 所有可能的分割方案。回文串 是正着读和反着读都一样的字符串。

    • 在for (int i = startIndex; i < s.size(); i++)循环中，我们 定义了起始位置startIndex，那么 [startIndex, i] 就是要截取的子串。首先判断这个子串是不是回文，如果是回文，就加入在vector path中，path用来记录切割过的回文子串。

    • class Solution {
public:
vector<vector<string>> res;
    vector<string> path;
    vector<vector<bool>> isP;
    void compP(const string& s){
        isP.resize(s.size(),vector<bool>(s.size(),false));
        for(int i=s.size()-1;i>=0;i--){
            for(int j=i;j<s.size();j++){
                if(j==i){
                    isP[i][j]=true;
                }else if(j-i==1){
                    isP[i][j]=(s[i]==s[j]);
                }else{
                    isP[i][j]=(s[i]==s[j]&&isP[i+1][j-1]);
                }
            }
        }
    }
    void track(const string &s,int start){
        if(start>=s.size()){
            res.push_back(path);
            return;
        }
        for(int i=start;i<s.size();i++){
            if(isP[start][i]){
                string str=s.substr(start,i-start+1);
                path.push_back(str);
            }else{
                continue;
            }
            track(s,i+1);
            path.pop_back();
        }
    }
    vector<vector<string>> partition(string s) {
        res.clear();
        path.clear();
        compP(s);
        track(s,0);
        return res;
    }
};

      • 1
      • 2
      • 3
      • 4
      • 5
      • 6
      • 7
      • 8
      • 9
      • 10
      • 11
      • 12
      • 13
      • 14
      • 15
      • 16
      • 17
      • 18
      • 19
      • 20
      • 21
      • 22
      • 23
      • 24
      • 25
      • 26
      • 27
      • 28
      • 29
      • 30
      • 31
      • 32
      • 33
      • 34
      • 35
      • 36
      • 37
      • 38
      • 39
      • 40
      • 41
      • 42
      • 43

    • 判断一个字符串是否是回文。可以使用双指针法，一个指针从前向后，一个指针从后向前，如果前后指针所指向的元素是相等的，就是回文字符串了。

    • bool isPalindrome(const string& s, int start, int end) {
   for (int i = start, j = end; i < j; i++, j--) {
       if (s[i] != s[j]) {
           return false;
       }
   }
   return true;
}

      • 1
      • 2
      • 3
      • 4
      • 5
      • 6
      • 7
      • 8

    • isPalindrome函数运用双指针的方法来判定对于一个字符串s, 给定起始下标和终止下标, 截取出的子字符串是否是回文字串。但是其中有一定的重复计算存在:例如给定字符串"abcde", 在已知"bcd"不是回文字串时, 不再需要去双指针操作"abcde"而可以直接判定它一定不是回文字串。

    • 具体来说, 给定一个字符串s, 长度为n, 它成为回文字串的充分必要条件是s[0] == s[n-1]且s[1:n-1]是回文字串。动态规划算法中, 我们可以高效地事先一次性计算出, 针对一个字符串s, 它的任何子串是否是回文字串, 然后在我们的回溯函数中直接查询即可, 省去了双指针移动判定这一步骤.

    题目：复原 IP 地址

    • 有效 IP 地址 正好由四个整数（每个整数位于 0 到 255 之间组成，且不能含有前导 0），整数之间用 '.' 分隔。 例如："0.1.2.201" 和 "192.168.1.1" 是 有效 IP 地址，但是 "0.011.255.245"、"192.168.1.312" 和 "192.168@1.1" 是 无效 IP 地址。

    • 给定一个只包含数字的字符串 s ，用以表示一个 IP 地址，返回所有可能的有效 IP 地址，这些地址可以通过在 s 中插入 '.' 来形成。你 不能 重新排序或删除 s 中的任何数字。你可以按 任何 顺序返回答案。

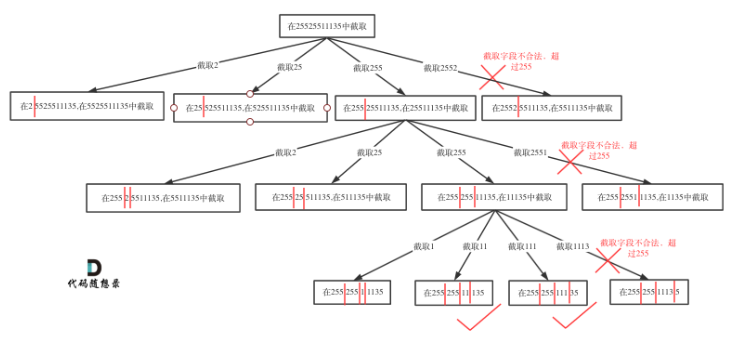
    • 切割问题可以抽象为树型结构，如图：

      • 在这里插入图片描述
    • class Solution {
public:
    vector<string> res;
    bool isV(const string &s,int start,int end){
        if(start>end){
            return false;
        }
        if(s[start]=='0'&& start!=end){// 0开头的数字不合法,纯0除外
            return false;
        }
        int num=0;
        for(int i=start;i<=end;i++){
            if(s[i]>'9'||s[i]<'0'){
                return false;
            }
            num =num*10+(s[i]-'0');
            if(num>255){
                return false;
            }
        }
        return true;
    }
    void track(string& s,int start,int pointnum){
        if(pointnum==3){
            if(isV(s,start,s.size()-1)){
                res.push_back(s);
            }
            return ;
        }

        for(int i=start;i<s.size();i++){
            if(isV(s,start,i)){
                s.insert(s.begin()+i+1,'.');
                pointnum++;
                track(s,i+2,pointnum);
                pointnum--;
                s.erase(s.begin()+i+1);
            }else{
                break;
            }
        }
    }
    vector<string> restoreIpAddresses(string s) {
        res.clear();
        if(s.size()<4||s.size()>12){
            return res;
        }
        track(s,0,0);
        return res;
    }
};

      • 1
      • 2
      • 3
      • 4
      • 5
      • 6
      • 7
      • 8
      • 9
      • 10
      • 11
      • 12
      • 13
      • 14
      • 15
      • 16
      • 17
      • 18
      • 19
      • 20
      • 21
      • 22
      • 23
      • 24
      • 25
      • 26
      • 27
      • 28
      • 29
      • 30
      • 31
      • 32
      • 33
      • 34
      • 35
      • 36
      • 37
      • 38
      • 39
      • 40
      • 41
      • 42
      • 43
      • 44
      • 45
      • 46
      • 47
      • 48
      • 49
      • 50
      • 51

    • 递归调用时，下一层递归的start要从i+2开始（因为需要在字符串中加入了分隔符.），同时记录分割符的数量pointnum 要 +1。回溯的时候，就将刚刚加入的分隔符. 删掉就可以了，pointnum也要-1。

    题目：子集

    • 给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。

    • 如果把 子集问题、组合问题、分割问题都抽象为一棵树的话，那么组合问题和分割问题都是收集树的叶子节点，而子集问题是找树的所有节点！其实子集也是一种组合问题，因为它的集合是无序的，子集{1,2} 和 子集{2,1}是一样的。

    • class Solution {
public:
    vector<vector<int>> res;
    vector<int> path;
    void track(vector<int> &nums,int start){
        res.push_back(path);
        if(start>=nums.size()){
            return;
        }
        for(int i=start;i<nums.size();i++){
            path.push_back(nums[i]);
            track(nums,i+1);
            path.pop_back();
        }
    }
    vector<vector<int>> subsets(vector<int>& nums) {
        res.clear();
        path.clear();
        track(nums,0);
        return res;
    }
};

      • 1
      • 2
      • 3
      • 4
      • 5
      • 6
      • 7
      • 8
      • 9
      • 10
      • 11
      • 12
      • 13
      • 14
      • 15
      • 16
      • 17
      • 18
      • 19
      • 20
      • 21
      • 22

    题目：子集 II

    • 给你一个整数数组 nums ，其中可能包含重复元素，请你返回该数组所有可能的子集（幂集）。解集 不能 包含重复的子集。返回的解集中，子集可以按 任意顺序 排列。

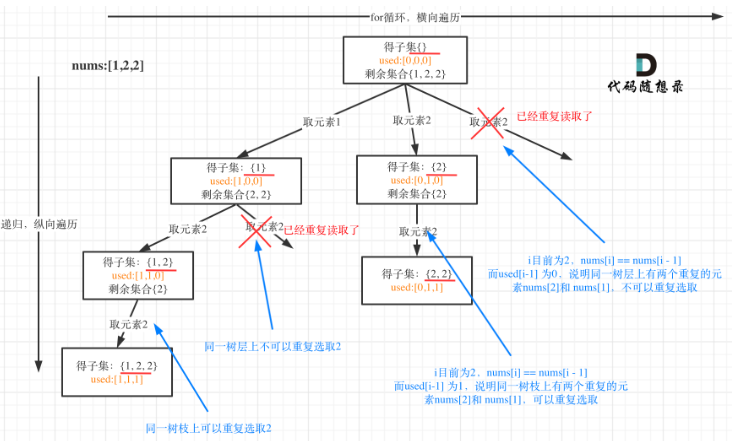
    • 在这里插入图片描述

    • 从图中可以看出，同一树层上重复取2 就要过滤掉，同一树枝上就可以重复取2，因为同一树枝上元素的集合才是唯一子集！

    • class Solution {
public:
    vector<vector<int>> res;
    vector<int> path;
    void track(vector<int> &nums,int start){
        res.push_back(path);
        unordered_set<int> uset;
        for(int i=start;i<nums.size();i++){
            if(uset.find(nums[i])!=uset.end()) continue;
            uset.insert(nums[i]);
            path.push_back(nums[i]);
            track(nums,i+1);
            path.pop_back();
        }
    }
    vector<vector<int>> subsetsWithDup(vector<int>& nums) {
        res.clear();
        path.clear();
        sort(nums.begin(),nums.end());
        track(nums,0);
        return res;
    }
};

      • 1
      • 2
      • 3
      • 4
      • 5
      • 6
      • 7
      • 8
      • 9
      • 10
      • 11
      • 12
      • 13
      • 14
      • 15
      • 16
      • 17
      • 18
      • 19
      • 20
      • 21
      • 22
      • 23

    • 不使用set去重

    •     void track2(vector<int>& nums,int start,vector<bool>& used){
        res.push_back(path);
        for(int i=start;i<nums.size();i++){
            if(i>0&&nums[i]==nums[i-1]&&used[i-1]==false) continue;
            path.push_back(nums[i]);
            used[i]=true;
            track2(nums,i+1,used);
            used[i]=false;
            path.pop_back();
        }
    }
    vector<vector<int>> subsetsWithDup(vector<int>& nums) {
        res.clear();
        path.clear();
        vector<bool> used(nums.size(),false);
        sort(nums.begin(),nums.end());
        track2(nums,0,used);
        return res;
    }

      • 1
      • 2
      • 3
      • 4
      • 5
      • 6
      • 7
      • 8
      • 9
      • 10
      • 11
      • 12
      • 13
      • 14
      • 15
      • 16
      • 17
      • 18
      • 19

    题目：递增子序列

    • 给你一个整数数组 nums ，找出并返回所有该数组中不同的递增子序列，递增子序列中 至少有两个元素 。你可以按 任意顺序 返回答案。数组中可能含有重复元素，如出现两个整数相等，也可以视作递增序列的一种特殊情况。

    • class Solution {
public:
    vector<vector<int>> res;
    vector<int> path;
    void track(vector<int>& nums,int start){
        if(path.size()>1){
            res.push_back(path);
        }
        unordered_set<int> uset;
        for(int i=start;i<nums.size();i++){
            if((!path.empty()&&nums[i]<path.back())||uset.find(nums[i])!=uset.end()){
                continue;
            }
            uset.insert(nums[i]);
            path.push_back(nums[i]);
            track(nums,i+1);
            path.pop_back();
        }
    }
    vector<vector<int>> findSubsequences(vector<int>& nums) {
        res.clear();
        path.clear();
        track(nums,0);
        return res;
    }
};

      • 1
      • 2
      • 3
      • 4
      • 5
      • 6
      • 7
      • 8
      • 9
      • 10
      • 11
      • 12
      • 13
      • 14
      • 15
      • 16
      • 17
      • 18
      • 19
      • 20
      • 21
      • 22
      • 23
      • 24
      • 25
      • 26

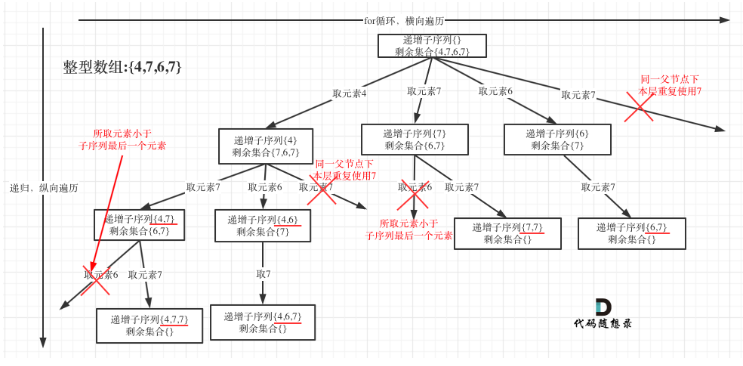
    • 在这里插入图片描述

    •     void track2(vector<int> &nums,int start){
        if(path.size()>1){
            res.push_back(path);
        }
        int used[201]={0};//数组中的整数范围是 [-100,100]。
        for(int i=start;i<nums.size();i++){
            if((!path.empty()&&nums[i]<path.back())||(used[nums[i]+100]==1)){
                continue;
            }
            used[nums[i]+100]=1;
            path.push_back(nums[i]);
            track2(nums,i+1);
            path.pop_back();
        }
    }
    vector<vector<int>> findSubsequences(vector<int>& nums) {
        res.clear();
        path.clear();
        track2(nums,0);
        return res;
    }

      • 1
      • 2
      • 3
      • 4
      • 5
      • 6
      • 7
      • 8
      • 9
      • 10
      • 11
      • 12
      • 13
      • 14
      • 15
      • 16
      • 17
      • 18
      • 19
      • 20
      • 21

    题目：全排列

    • 给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

    • 首先排列是有序的，也就是说 [1,2] 和 [2,1] 是两个集合，这和之前分析的子集以及组合所不同的地方。可以看出元素1在[1,2]中已经使用过了，但是在[2,1]中还要在使用一次1，所以处理排列问题就不用使用start了。但排列问题需要一个used数组，标记已经选择的元素，如图橘黄色部分所示:

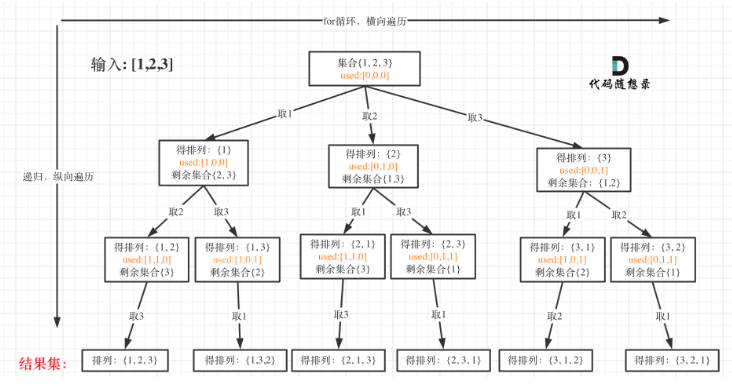
    • 在这里插入图片描述

    • 因为排列问题，每次都要从头开始搜索，例如元素1在[1,2]中已经使用过了，但是在[2,1]中还要再使用一次1。而used数组，其实就是记录此时path里都有哪些元素使用了，一个排列里一个元素只能使用一次。

    • class Solution {
public:
    vector<vector<int>> res;
    vector<int> path;
    void track(vector<int> &nums,vector<bool> &used){
        if(path.size()==nums.size()){
            res.push_back(path);
            return;
        }
        for(int i=0;i<nums.size();i++){
            if(used[i]==true) continue;
            used[i]=true;
            path.push_back(nums[i]);
            track(nums,used);
            used[i]=false;
            path.pop_back();
        }
    }
    vector<vector<int>> permute(vector<int>& nums) {
        res.clear();
        path.clear();
        vector<bool> used(nums.size(),false);
        track(nums,used);
        return res;
    }
};

      • 1
      • 2
      • 3
      • 4
      • 5
      • 6
      • 7
      • 8
      • 9
      • 10
      • 11
      • 12
      • 13
      • 14
      • 15
      • 16
      • 17
      • 18
      • 19
      • 20
      • 21
      • 22
      • 23
      • 24
      • 25
      • 26

    • 时间复杂度: O(n!)；空间复杂度: O(n)。排列问题的不同：每层都是从0开始搜索而不是start，需要used数组记录path里都放了哪些元素了

    题目：全排列 II

    • 给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。

    • class Solution {
public:
    vector<vector<int>> res;
    vector<int> path;
    void track(vector<int> &nums,vector<bool> &used){
        if(path.size()==nums.size()){
            res.push_back(path);
            return;
        }
        for(int i=0;i<nums.size();i++){
            if((i>0 && nums[i]==nums[i-1]) && used[i-1]==false){
                continue;
            }
            if(used[i]==true){
                continue;
            }
            used[i]=true;
            path.push_back(nums[i]);
            track(nums,used);
            used[i]=false;
            path.pop_back();
        }
    }
    vector<vector<int>> permuteUnique(vector<int>& nums) {
        res.clear();
        path.clear();
        sort(nums.begin(),nums.end());
        vector<bool> used(nums.size(),false);
        track(nums,used);
        return res;
    }
};

      • 1
      • 2
      • 3
      • 4
      • 5
      • 6
      • 7
      • 8
      • 9
      • 10
      • 11
      • 12
      • 13
      • 14
      • 15
      • 16
      • 17
      • 18
      • 19
      • 20
      • 21
      • 22
      • 23
      • 24
      • 25
      • 26
      • 27
      • 28
      • 29
      • 30
      • 31
      • 32

    • 还要强调的是去重一定要对元素进行排序，这样我们才方便通过相邻的节点来判断是否重复使用了。

    • 在这里插入图片描述

    • 图中我们对同一树层，前一位（也就是nums[i-1]）如果使用过，那么就进行去重。一般来说：组合问题和排列问题是在树形结构的叶子节点上收集结果，而子集问题就是取树上所有节点的结果。时间复杂度: O(n! * n)

  • 相关阅读:
    比特币是如何转账的——比特币区块链的五个技术性细节
    文心一言 VS 讯飞星火 VS chatgpt （102）-- 算法导论9.3 8题
    OSPF原理
    Nodejs 第七十九章（Kafka进阶）
    算法读书笔记-3
    SD NAND 的 SDIO在STM32上的应用详解(上篇）
    【Java基础】集合容器
    Paper Time｜开放式时空大数据助力智能公交路线规划
    在线教育行业介绍
    c-const修饰指针-day16
  • 原文地址：https://blog.csdn.net/weixin_43424450/article/details/134028857