LeetCode 11. 盛最多水的容器

盛水最多的容器

题目链接 11. 盛最多水的容器

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

**说明：**你不能倾斜容器。

示例 1：

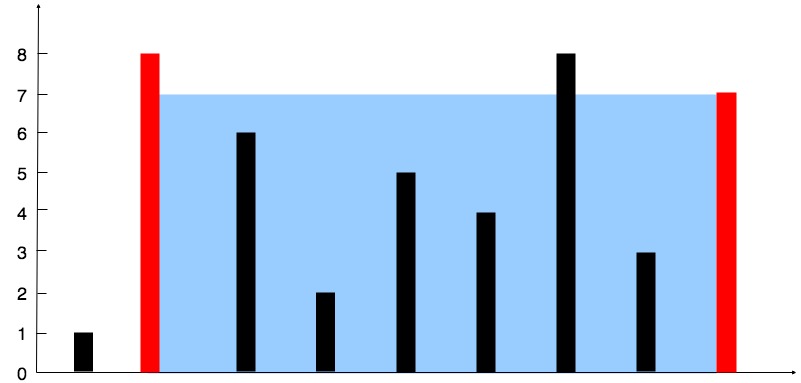
输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。
1
2
3

示例 2：

输入：height = [1,1]
输出：1
1
2

题目解释

就是求我们水桶的最大的容量,其中高度是我们左右两个元素的较小值,宽度是对应元素下标的差值.

算法原理

一般情况下,我们可以使用暴力求解.不过这里暴力求解是会超时的.这里我们也是使用双指针.我们先看一个情况.

V = v = (right - left) * min(height[right], height[left])
1

我们固定左右的位置,这里假设num[left] < num[right],下面我们该如何移动我们的left和right,存在下面两种

• left向右移
• right向左移

首先我们要确定的是无论上面如何移动,那么我们的宽度一定是减少的,如果我们想要较大的容量,只能寄托于我们的高度提升.

对于left右移,这里有可能高度会提升,毕竟我们的原本的高度是height[left].但是如果我们right右移,此时我们对于right-1的元素会有三个情况

• height[right-1] > height[left]
• height[right-1] == height[left]
• height[right-1] < height[left]

但是,无论从哪一个角度出发,我们移动right的得到的容量都比原本的要小

细节补充

补充一下,我们上面举了一个例子,我们每一次的移动都是希望我们下一次的容量比当前容量更大,至于那些一定比我们当前小的,那么就直接舍弃

代码编写

class Solution {
public:
    int maxArea(vector& height) {
        int left = 0;
        int right = height.size() -1;
        int result = 0;
        while(left < right)
        {
            result = max(result, (right-left)*min(height[left], height[right]));
            if(height[left] < height[right]) left++;
            else right--;
        }
        return result;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15