【算法训练-动态规划 一】【应用DP问题】零钱兑换、爬楼梯、买卖股票的最佳时机I、打家劫舍

废话不多说，喊一句号子鼓励自己：程序员永不失业，程序员走向架构！本篇Blog的主题是【动态规划】，使用【数组】这个基本的数据结构来实现，这个高频题的站点是：CodeTop，筛选条件为：目标公司+最近一年+出现频率排序，由高到低的去牛客TOP101去找，只有两个地方都出现过才做这道题（CodeTop本身汇聚了LeetCode的来源），确保刷的题都是高频要面试考的题。明确目标题后，附上题目链接，后期可以依据解题思路反复快速练习，题目按照题干的基本数据结构分类，且每个分类的第一篇必定是对基础数据结构的介绍。

零钱兑换【MID】

通过这道题推导下动态规划状态转移方程的推导思路

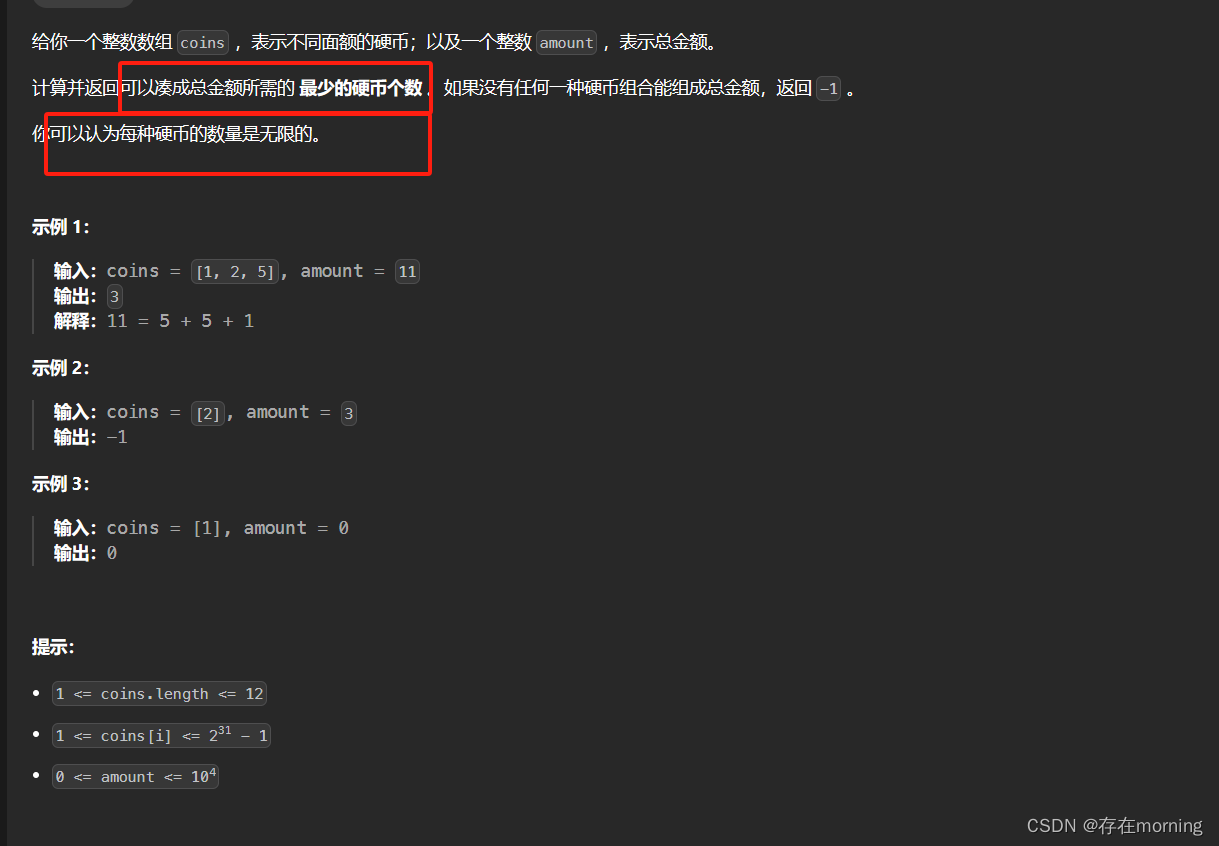
题干

回溯的思路就是：无重复可复选的组合树解法

解题思路

先分析明确 这个问题可以用动态规划解决

问题分析

首先，这个问题是动态规划问题，因为它具有「最优子结构」的。要符合「最优子结构」，子问题间必须互相独立【无后效性】。

什么是相互独立，比如说，假设你考试，每门科目的成绩都是互相独立的。你的原问题是考出最高的总成绩，那么你的子问题就是要把语文考到最高，数学考到最高…… 为了每门课考到最高，你要把每门课相应的选择题分数拿到最高，填空题分数拿到最高…… 当然，最终就是你每门课都是满分，这就是最高的总成绩。得到了正确的结果：最高的总成绩就是总分。因为这个过程符合最优子结构，「每门科目考到最高」这些子问题是互相独立，互不干扰的。但是，如果加一个条件：你的语文成绩和数学成绩会互相制约，不能同时达到满分，数学分数高，语文分数就会降低，反之亦然。这样的话，显然你能考到的最高总成绩就达不到总分了，按刚才那个思路就会得到错误的结果。因为「每门科目考到最高」的子问题并不独立，语文数学成绩户互相影响，无法同时最优，所以最优子结构被破坏。

回到凑零钱问题，为什么说它符合最优子结构呢？假设你有面值为 1, 2, 5 的硬币，你想求 amount = 11 时的最少硬币数（原问题），如果你知道凑出 amount = 10, 9, 6 的最少硬币数（子问题），你只需要把子问题的答案加一（再选一枚面值为 1, 2, 5 的硬币），求个最小值，就是原问题的答案。因为硬币的数量是没有限制的，所以子问题之间没有相互制约，是互相独立的

如何列出状态转移方程

那么，既然知道了这是个动态规划问题，就要思考如何列出正确的状态转移方程？

1. 确定 base case，这个很简单，显然目标金额 amount 为 0 时算法返回 0，因为不需要任何硬币就已经凑出目标金额了。
2. 确定「状态」，也就是原问题和子问题中会变化的变量。由于硬币数量无限，硬币的面额也是题目给定的，只有目标金额会不断地向 base case 靠近，所以唯一的「状态」就是目标金额 amount。
3. 确定「选择」，也就是导致「状态」产生变化的行为。目标金额为什么变化呢，因为你在选择硬币，你每选择一枚硬币，就相当于减少了目标金额。所以说所有硬币的面值，就是你的「选择」。
4. 明确 dp 函数/数组的定义。我们采用动态规划，自底向上求解，所以dp 数组的定义：当目标金额为 i 时，至少需要 dp[i] 枚硬币，例如目标金额为11时，至少需要dp[11]种硬币组合

代码实现

给出代码实现基本档案

基本数据结构：数组
辅助数据结构：无
算法：动态规划
技巧：无

import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 最少货币数
     * @param arr int整型一维数组 the array
     * @param aim int整型 the target
     * @return int整型
     */
    public int coinChange(int[] coins, int amount) {
        // 0 异常情况
        if (coins.length == 0 || amount < 0) {
            return -1;
        }
        // 1 定义动态规划数组，dp[i] 表示组成目标金额i【状态】的最少货币数量【选择】
        int[] dp = new int[amount + 1];
        // 所有数值初始化为目标金额，初始化目标金额最多有amount种组合（当货币为1时）
        Arrays.fill(dp, amount+1);
       
        // 2 定义base case :目标金额为0 需要的货币数量为0
        dp[0] = 0;

        // 3 列举所有状态，求每种状态的最少货币选择
        for (int i = 1; i < dp.length; i++) {
            // 内层 for 循环在求所有选择的最小值
            for (int coin : coins) {
                // 剪枝，如果目标金额小于coin，则没有任何选择，子问题无解
                if (i < coin) {
                    continue;
                }
                // 状态转移方程，目标金额的货币组合数=1（当前货币占用1个组合位置）+dp[i-coin](差额前值的最少组合数)
                dp[i] = Math.min(dp[i], dp[i - coin] + 1);
            }
        }
        // 如果金额为10的选择大于10种（例如11种），那会出现不足1元的币种，显然不满足条件
        return dp[amount] > amount? -1: dp[amount];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

为啥 dp 数组中的值都初始化为 amount + 1 呢，因为凑成 amount 金额的硬币数最多只可能等于 amount（全用 1 元面值的硬币），所以初始化为 amount + 1 就相当于初始化为正无穷，便于后续取最小值，如果没有取到最小值（没有更改初始化的值）则认为没有找到最少的组合方式

为啥不直接初始化为 int 型的最大值 Integer.MAX_VALUE 呢？因为后面有 dp[i - coin] + 1，这就会导致整型溢出

复杂度分析

时间复杂度：O(S*n)，其中 S 是金额，n 是面额数。我们一共需要计算 O(S)个状态，S 为题目所给的总金额。对于每个状态，每次需要枚举 n 个面额来转移状态，所以一共需要 O(S*n) 的时间复杂度。

空间复杂度：O(S)。数组 dp 需要开长度为总金额 S 的空间。

爬楼梯【EASY】

再来一道动规里相对来说较为基础的题目

题干

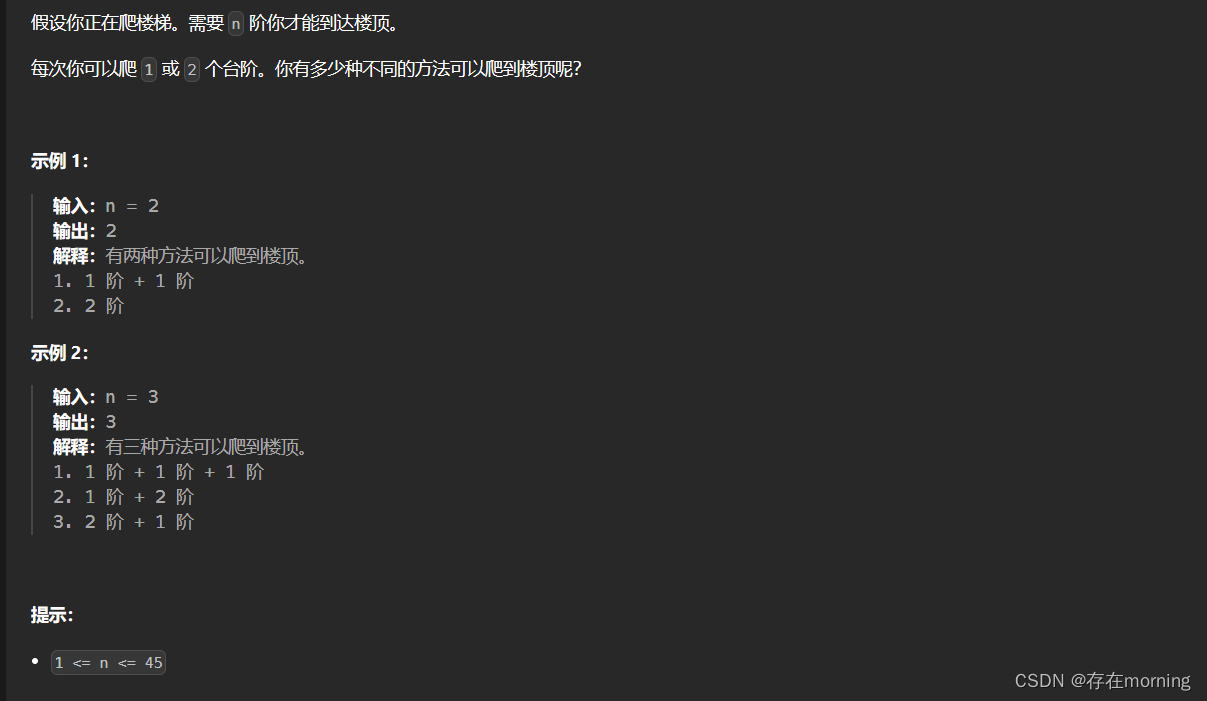
和零钱兑换类似，不过和零钱兑换不同的是，要记录的是兑换的方法有多少种，而不是最少数量的组合

解题思路

动态规划，定义状态转移公式：dp[i]=dp[i-1]+dp[i-2]

代码实现

给出代码实现基本档案

基本数据结构：数组
辅助数据结构：无
算法：动态规划
技巧：无

import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param number int整型
     * @return int整型
     */
    public int climbStairs(int n) {
        // 1 特殊情况判断，如果目标台阶数为0，则有0种跳法
        if (n < 1) {
            return 0;
        }

        // 2 定义状态转移表,dp[i]表示跳上i级台阶总共有dp[i]种跳法
        int[] dp = new int[n + 1];

        // 3 定义base case:因为一次只能跳1或2，所以初始状态为dp[0],dp[1]
        dp[0] = 1;
        dp[1] = 1;

        // 4 进行状态转移，穷举所有状态对应的跳法
        for (int i = 2; i < dp.length; i++) {
            dp[i] = dp[i - 1] + dp[i - 2];
        }


        return dp[n];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

复杂度分析

时间复杂度为：O（N）：迭代此时为N
空间复杂度为：O（N）：状态转移表的大小为N

还有一种压缩空间复杂度的写法，就是用滚动数组

import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param number int整型
     * @return int整型
     */
    public int climbStairs(int n) {
        // 1 特殊情况判断，如果目标台阶数为0，则有0种跳法
        if (n == 0 || n == 1) {
            return 1;
        }

        int first = 1;
        int second = 1;
        int result = 0;

        // 2 数组滚动更新
        for (int i = 2; i <= n; i++) {
            result = first + second;
            first = second;
            second = result;
        }


        return result;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

空间复杂度可以降到O（1），但是没有普适性。

买卖股票的最佳时机I【EASY】

来从动态规划最简单的题开始训练

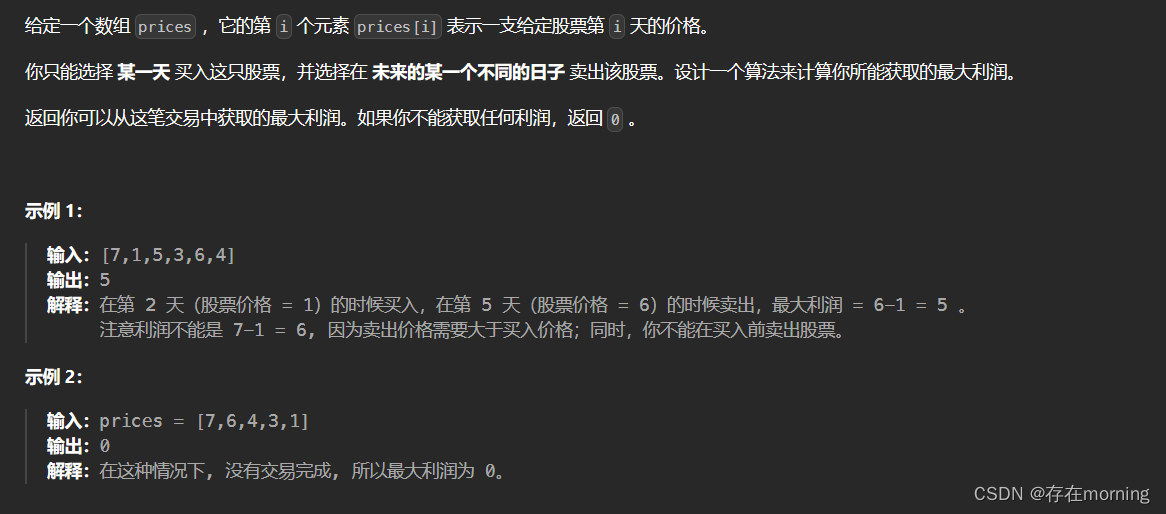
题干

解题思路

按照动态规划的思路进行状态设计和状态转移方程编写

1 定义状态（定义子问题）

dp[i]：表示第i天卖出股票的最大利润。

2 状态转移方程（描述子问题之间的联系）

根据状态的定义，由于 prices[i] 一定会被选取，并且以 prices[i] 结尾的卖出日期与以 prices[i - 1] 结尾的卖出日期只相差一个元素 nums[i] 。假设数组 prices的值全都严格大于 0，那么一定有 dp[i] = dp[i - 1] + prices[i]-prices[i-1]。可是 dp[i - 1] 有可能是负数，于是分类讨论：

• 如果 dp[i - 1] > 0，那么可以把prices[i]-prices[i-1]直接接在 dp[i - 1] 表示的那个数组的后面，得到和更大的利润；
• 如果 dp[i - 1] <= 0，那么 prices[i] 加上前面的数 dp[i - 1] 以后值不会变大。于是 dp[i] 「另起炉灶」，此时单独的利润prices[i]-prices[i-1]的值，就是 dp[i]。

以上两种情况的最大值就是 dp[i] 的值

3 初始化状态

dp[0] 根据定义，初始化第1天买入第一天卖出利润为0，初始化利润值

4 求解方向

这里采用自底向上，从最小的状态开始求解

5 找到最终解

这里的dp[i]只是第i天卖出的最大利润，并不是题目中的问题，买卖股票的最大利润，所以最终解并不是子问题的解，需要用一个MAX值承载，通过与dp[i]比较更新最终解

代码实现

给出代码实现基本档案

基本数据结构：数组
辅助数据结构：无
算法：动态规划
技巧：无

其中数据结构、算法和技巧分别来自：

• 10 个数据结构：数组、链表、栈、队列、散列表、二叉树、堆、跳表、图、Trie 树
• 10 个算法：递归、排序、二分查找、搜索、哈希算法、贪心算法、分治算法、回溯算法、动态规划、字符串匹配算法
• 技巧：双指针、滑动窗口、中心扩散

当然包括但不限于以上

import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param prices int整型一维数组
     * @return int整型
     */
    public int maxProfit (int[] prices) {
        // 1 初始化动态规划数组：维护第i天卖出的最大利润
        int[] dp = new int[prices.length];
        int maxValue = dp[0];
        for (int i = 1; i < prices.length; i++) {
            // 2 计算当前天和前一天卖出的利润差
            int curValue = prices[i] - prices[i - 1];
            // 3 状态转移方程：第i天卖出的最大利润为：如果i-1天卖出的最大利润为负数，则舍弃，否则累加第i天的最大利润
            dp[i] = dp[i - 1] <= 0 ? curValue : dp[i - 1] + curValue;
            // 4 每次计算完最小问题后更新最大值
            maxValue = Math.max(dp[i], maxValue);
        }
        return maxValue;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

复杂度分析

时间复杂度：遍历了一遍数组，所以时间复杂度为O（N）
空间复杂度：定义了动规数组，空间复杂度为O（N）

打家劫舍【MID】

来一道MID的题目，打家劫舍，也是耳闻已久的题目了

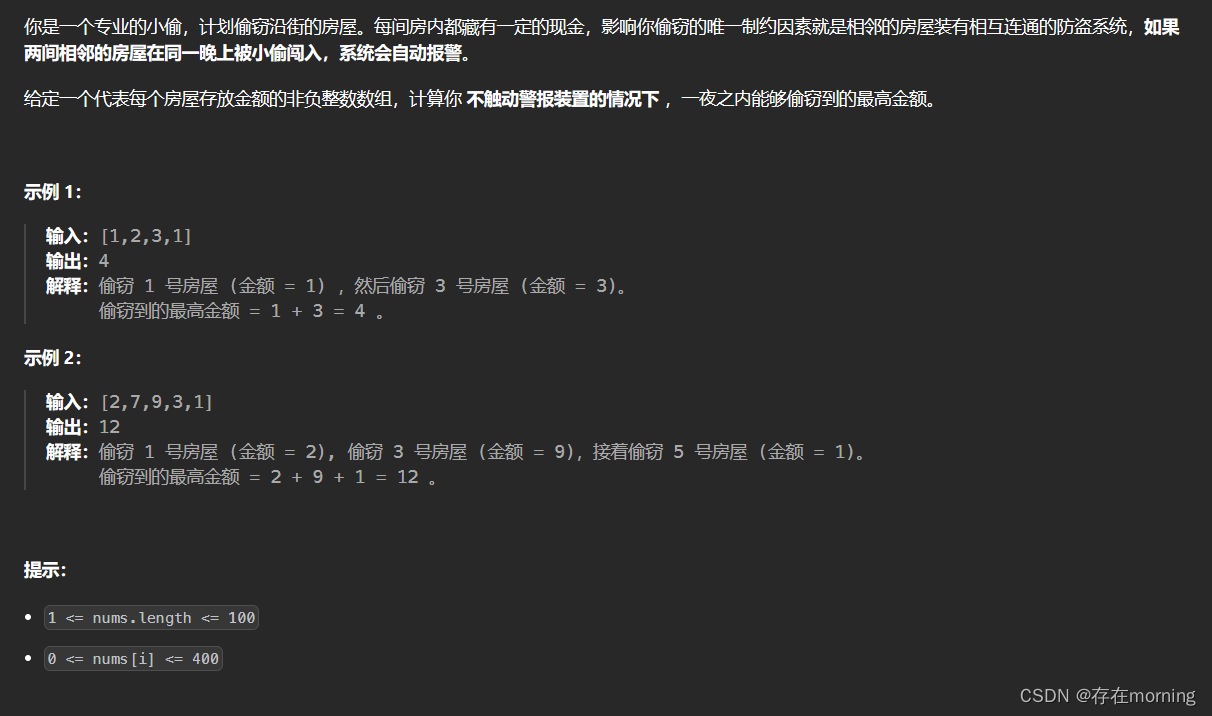
题干

解题思路

还是用动态规划的方式解题

1 定义状态（定义子问题）

子问题是和原问题相似，但规模较小的问题。例如这道小偷问题，原问题是 “从全部房子中能偷到的最大金额”，将问题的规模缩小，子问题就是 “从 i个房子中能按照规则偷到的最大金额 ”，

dp[i]：表示能按照规则从i间房子所能偷到的最大利润。

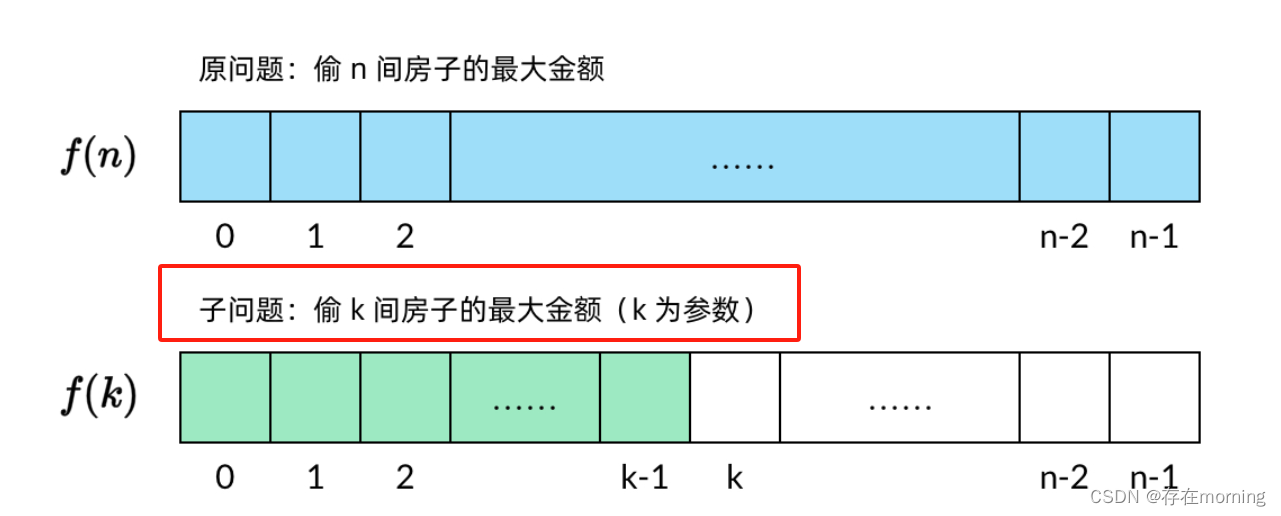
2 状态转移方程（描述子问题之间的联系）

3 初始化状态

这里采用自底向上，从最小的状态开始求解

• 当k=0时，没有房子，所以dp[0]=0;
• 当k=1时，有一间房子，所以只能偷这个，金额为dp[1]=nums[0]

5 找到最终解

代码实现

给出代码实现基本档案

基本数据结构：数组
辅助数据结构：无
算法：动态规划
技巧：无

其中数据结构、算法和技巧分别来自：

• 10 个数据结构：数组、链表、栈、队列、散列表、二叉树、堆、跳表、图、Trie 树
• 10 个算法：递归、排序、二分查找、搜索、哈希算法、贪心算法、分治算法、回溯算法、动态规划、字符串匹配算法
• 技巧：双指针、滑动窗口、中心扩散

当然包括但不限于以上

import java.util.*;

class Solution {
    public int rob(int[] nums) {
        // 1 特殊情况处理，如果不存在房间，只能偷到0元
        if (nums.length < 1) {
            return 0;
        }

        // 2 定义状态转移表:dp[i] 表示偷窃前i间房子中的最大金额，原问题为偷窃全部房间的最大金额nums.length
        int[] dp = new int[nums.length + 1];

        // 3 初始化base case,前0间房，金额为0，第一间房的金额就是nums[0]
        dp[0] = 0;
        dp[1] = nums[0];


        // 4 定义状态转移方程
        for (int i = 2; i <dp.length; i++) {
            // 前i间房子的偷窃最大金额=（前i-2间房子最大值+第i间房子）与（前i-1间房子的最大值）
            dp[i] = Math.max(dp[i - 2] + nums[i - 1], dp[i - 1]);
        }

        return dp[nums.length];

    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

为了便于理解，补充一个合nums数组下标对齐的版本

import java.util.*;

class Solution {
    public int rob(int[] nums) {
        // 1 特殊情况处理，如果不存在房间，只能偷到0元
        if (nums.length < 1) {
            return 0;
        }

        // 2 定义状态转移表:dp[i] 表示偷窃前i间房子中的最大金额，原问题为偷窃全部房间的最大金额nums.length-1
        int[] dp = new int[nums.length];

        // 3 初始化base case,前0间房，金额为0，第一间房的金额就是nums[0]
        if (nums.length == 1) {
            return nums[0];
        }
        if (nums.length == 2) {
            return Math.max(nums[1], nums[0]);
        }
        dp[0] = nums[0];
        dp[1] = Math.max(nums[1], nums[0]);


        // 4 定义状态转移方程
        for (int i = 2; i < dp.length; i++) {
            // 前i间房子的偷窃最大金额=（前i-2间房子最大值+第i间房子）与（前i-1间房子的最大值）
            dp[i] = Math.max(dp[i - 2] + nums[i], dp[i - 1]);
        }

        return dp[nums.length - 1];

    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

复杂度分析

时间复杂度：遍历了一遍数组，所以时间复杂度为O（N）
空间复杂度：定义了动规数组，空间复杂度为O（N）

拓展知识：动态规划与贪心算法

动态规划

动态规划（Dynamic Programming，简称DP）是一种解决复杂问题的算法设计技术，常用于优化问题和组合问题的求解。它通过将原问题分解成子问题，并保存子问题的解，以避免重复计算，从而提高算法的效率。动态规划通常用于解决具有重叠子问题和最优子结构性质的问题。

动态规划的基本思想可以总结为以下几个步骤：

1. 定义问题的状态：首先要明确定义问题的状态，这些状态可以用来描述问题的各种情况。

2. 找到状态转移方程：状态转移方程描述了问题之间的联系，即如何从一个状态转移到另一个状态。这通常涉及到问题的递归关系，通过这个关系可以从较小规模的子问题得到更大规模的问题的解。

3. 初始化状态：确定初始状态的值，这通常是问题规模最小的情况下的解。

4. 自底向上或自顶向下求解：动态规划可以采用自底向上（Bottom-Up）或自顶向下（Top-Down）的方式求解问题。自底向上是从最小的状态开始逐步计算，直到得到最终问题的解；自顶向下是从最终问题开始，递归地计算子问题的解，直到达到最小状态。

5. 根据问题的要求，从状态中找到最终解。

动态规划常见的应用领域包括：

1. 最长公共子序列问题：在两个序列中找到一个最长的共同子序列，用于比较字符串相似性。

2. 背包问题：在给定一定容量的背包和一组物品的情况下，选择一些物品放入背包，使得物品的总价值最大或总重量不超过背包容量。

3. 最短路径问题：求解图中两点之间的最短路径，如Dijkstra算法和Floyd-Warshall算法。

4. 硬币找零问题：给定一组硬币面额和一个目标金额，找到使用最少数量的硬币组合成目标金额。

5. 斐波那契数列问题：求解斐波那契数列的第n个数，通过动态规划可以避免重复计算。

动态规划是一种强大的问题求解方法，但它并不适用于所有类型的问题。在使用动态规划时，需要仔细分析问题的性质，确保问题具有重叠子问题和最优子结构性质，以确保动态规划算法能够有效地解决问题。

贪心算法

贪心算法（Greedy Algorithm）是一种常用的问题求解策略，通常用于解决最优化问题，如最短路径、最小生成树、背包问题等。贪心算法的基本思想是每一步都选择当前状态下的最优解，而不考虑全局的最优解，希望通过局部最优的选择最终达到全局最优。贪心算法通常是一种高效的方法，但并不是所有问题都适合使用贪心算法，因为有些问题的最优解不一定可以通过贪心选择得到。

贪心算法的一般步骤如下：

1. 定义问题的优化目标，明确问题的约束条件。

2. 从问题的初始状态开始，通过一系列选择，每次选择局部最优解，更新当前状态。

3. 检查是否满足问题的约束条件和终止条件。如果不满足，则回到第2步继续选择；如果满足，则算法结束。

4. 对于某些问题，需要证明贪心选择的局部最优解确实能够导致全局最优解，这需要数学证明或者举出反例。

以下是一些常见的问题，可以使用贪心算法解决：

1. 最小生成树问题：如Kruskal算法和Prim算法用于寻找无向图中的最小生成树。

2. 最短路径问题：如Dijkstra算法用于寻找图中两点之间的最短路径。

3. 背包问题：如分数背包问题和0/1背包问题，可以使用贪心算法进行求解。

4. 活动选择问题：如贪心选择活动安排最多的问题，可以使用贪心算法求解。

需要注意的是，并非所有问题都适合使用贪心算法，因为有些问题的最优解可能需要全局搜索或者动态规划等其他算法。因此，在应用贪心算法之前，需要仔细分析问题的特点和性质，以确定贪心算法是否合适。

动态规划与贪心算法区别

动态规划（Dynamic Programming）和贪心算法（Greedy Algorithm）都是常见的问题求解策略，但它们在问题求解时有很大的区别，适用于不同类型的问题和场景。

区别：

1. 最优子结构性质：

   • 动态规划：动态规划问题通常具有最优子结构性质，即全局最优解可以通过子问题的最优解来构造。动态规划通常涉及到将问题划分为重叠的子问题，然后利用这些子问题的解来构建全局最优解。
   • 贪心算法：贪心算法通常涉及到每一步选择当前状态下的最优解，但不一定具有最优子结构性质。贪心算法通常是通过一系列局部最优选择来达到全局最优，但不能保证一定能够得到全局最优解。

2. 选择的灵活性：

   • 动态规划：在动态规划中，可以在每个子问题中考虑多种选择，并计算每种选择的代价或价值，然后选择最优的。通常需要一个状态转移方程来描述问题的子结构和递归关系。
   • 贪心算法：贪心算法在每一步都选择当前状态下的最优解，不考虑其他选择的影响。它通常适用于问题具有"贪心选择性质"的情况，即通过局部最优选择能够得到全局最优解。

问题解决场景：

1. 动态规划适用场景：

   • 当问题的最优解可以通过子问题的最优解来构造时，通常使用动态规划。典型问题包括：
     • 最短路径问题（如Dijkstra算法）
     • 最长公共子序列问题
     • 背包问题（如0/1背包问题）
     • 编辑距离问题
   • 需要存储和重用子问题的解，通常使用表格或数组来实现。

2. 贪心算法适用场景：

   • 当问题具有贪心选择性质，即通过每一步的局部最优选择能够达到全局最优时，可以使用贪心算法。典型问题包括：
     • 最小生成树问题（如Prim算法和Kruskal算法）
     • 哈夫曼编码问题
     • 活动选择问题
     • 货币找零问题
   • 贪心算法通常更简单和高效，但不能解决所有问题，因为它没有全局的视野。

总之，动态规划和贪心算法是两种不同的问题求解策略，根据问题的特性和要求选择合适的算法非常重要。有些问题可以同时使用这两种策略的思想，即使用贪心算法的局部最优性来设计动态规划的状态转移方程。