【电路笔记】-平均电压和均方根电压（RMS Voltage）

平均电压和均方根电压（RMS Voltage）

1、概述

在 DC 状态下，只能对电压值进行一种定义，该值是明确的，并且由参考值 0 V 与 DC 信号的平线图之间的差异确定。然而，在 AC 状态下， 仅提及一个电压值可能会导致混乱。 从一个简单的正弦波形，我们至少可以列出四种不同的电压定义：

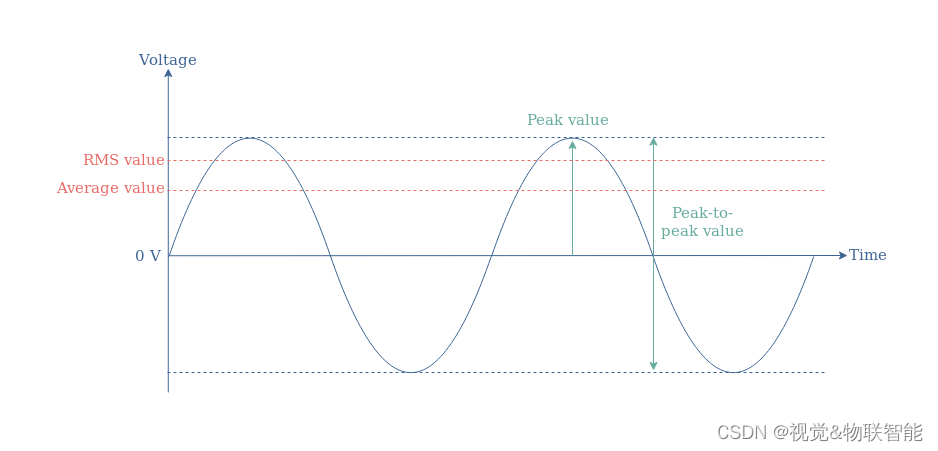
图 1：峰值(Peak Value)、平均值(Average Value)和RMS(均方根值)

峰值(Peak Value)对应于参考值（即交流信号振荡的值）与信号最大值之间的差值。 峰峰值是峰值乘以因子2，它对应于信号的总垂直宽度。

在图1中，我们还用红色突出显示了平均值和RMS值，这是我们将重点关注的本文中的两节将分别介绍平均值和RMS值，我们将了解它们是如何定义的，如何确定它们，最后我们将了解 RMS 值的特殊之处。

2、平均电压

对于基本的对称正弦波、三角波、方波或锯齿波（参见图 2 和交流波形教程），很难说清楚平均电压值，我们将在下面标记 A。 事实上，这些类型的信号在其周期的一半期间为正，在另一半期间为负。 换句话说，信号 50% 的时间位于水平轴上方，50% 的时间位于水平轴下方。根据该观察，很容易理解，如果我们考虑整个周期上任何这些信号的平均值，则为 等于 0，无论峰值如何，因此不相关。

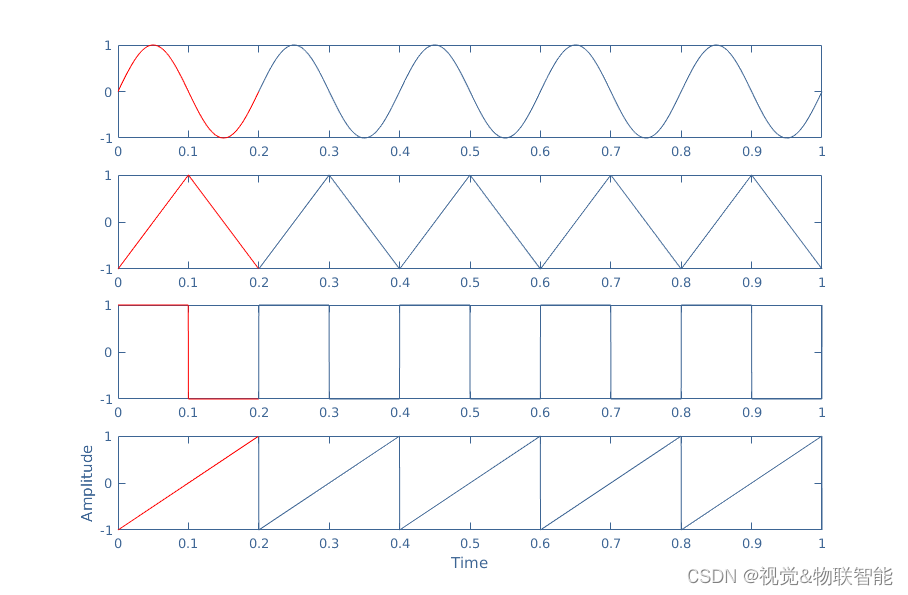
图 2：基本正弦波、三角波、方波和锯齿波

我们可以通过解释如何计算平均值来证明这个结果。 对于有限的一组值，平均过程包括将所有值（V1、V2、V3…）相加，然后除以该组的基数 N（该组中有多少个值）：

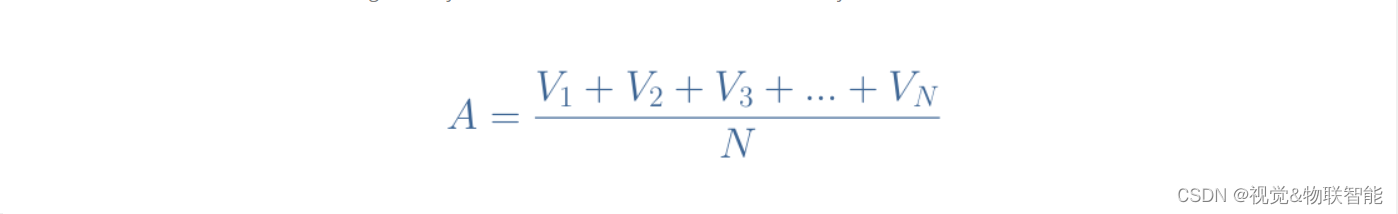
然而，对于模拟信号来说，不可能简单地对信号在一个周期内获取的所有瞬时值（也称为中坐标）求和，因为存在无穷大。 我们不使用求和，而是使用积分运算：

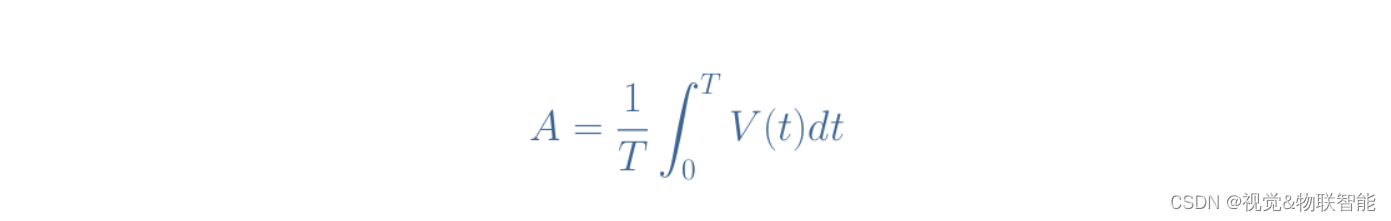
公式 1：整个周期内的交流信号 V(t) 的平均值

对于如图 1 所示的基本波形，我们可以看到该公式的第一项和第二项相等但符号相反，因此平均值等于 0。

为了使这些信号的平均值有意义，我们更愿意分别考虑半个正周期和半个负周期，它们的一些值分别在下图 3 中以红色和绿色突出显示：

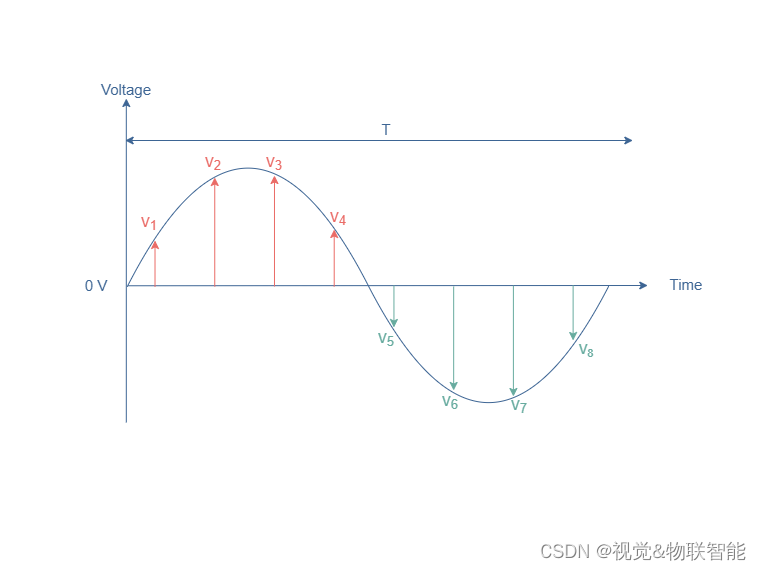
图 3：正弦波形的正半周期（红色）和负半周期（绿色）的一些瞬时值

与公式 1 类似，我们可以分别定义正半周期 (A+) 和负半周期 (A–) 的平均值：

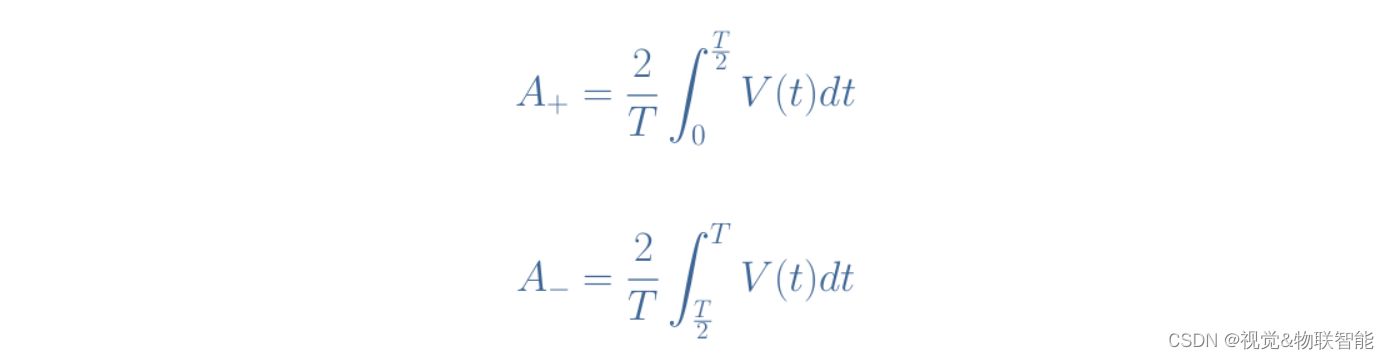
公式3：正 (+) 和负 (-) 半周期的交流信号 V(t) 的平均值

$A_{+}$和$A_{–}$的值取决于我们正在处理的信号及其各自的峰值 ($V_p$)。 我们在下面列出了绝对值 |A| 最常见的基本和对称交流信号的 $A_{+}$ 和