-
【数据结构与算法】two X 树的遍历以及功能实现
前言:前面我们已经提到过树、二叉树的概念及结构、堆排序、Top-k问题等的知识点,这篇文章我们来详解一下二叉树的链式结构等问题。
目录
二叉树结构定义(struct BinaryTreeNode)
判断一棵树是否为完全二叉树(BinaryTreeComplete)
一.链式二叉树存储的概念
二叉树的链式存储结构是指: 用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。通常的方法是链表中每个结点由三个域组成, 数据域和左右指针域,左右指针分别用来给出该结点 左孩子和右孩子所在的链结点的存储地址 。链式结构又分为二叉链和三叉链,当前我们学习中一般都是二叉链,后面课程学到高阶数据结构如红黑树等会用到三叉链。
2.1 前置说明
在学习二叉树的基本操作前,需先要创建一棵二叉树,然后才能学习其相关的基本操作。由于现在大家对二叉树结构掌握还不够深入,为了降低大家学习成本,此处手动快速创建一棵简单的二叉树,快速进入二叉树操作学习,等二叉树结构了解的差不多时,我们反过头再来研究二叉树真正的创建方式。- typedef int BTDataType;
- typedef struct BinaryTreeNode
- {
- BTDataType data;
- struct BinaryTreeNode* left;
- struct BinaryTreeNode* right;
- }BTNode;
- BTNode* BuyNode(BTDataType x)
- {
- BTNode* node = (BTNode*)malloc(sizeof(BTNode));
- if (node == NULL)
- {
- perror("malloc fail");
- return NULL;
- }
- node->data = x;
- node->left = NULL;
- node->right = NULL;
- return node;
- }
- BTNode* CreatBinaryTree()
- {
- BTNode* node1 = BuyNode(1);
- BTNode* node2 = BuyNode(2);
- BTNode* node3 = BuyNode(3);
- BTNode* node4 = BuyNode(4);
- BTNode* node5 = BuyNode(5);
- BTNode* node6 = BuyNode(6);
- node1->left = node2;
- node1->right = node4;
- node2->left = node3;
- node4->left = node5;
- node4->right = node6;
- return node1;
- }
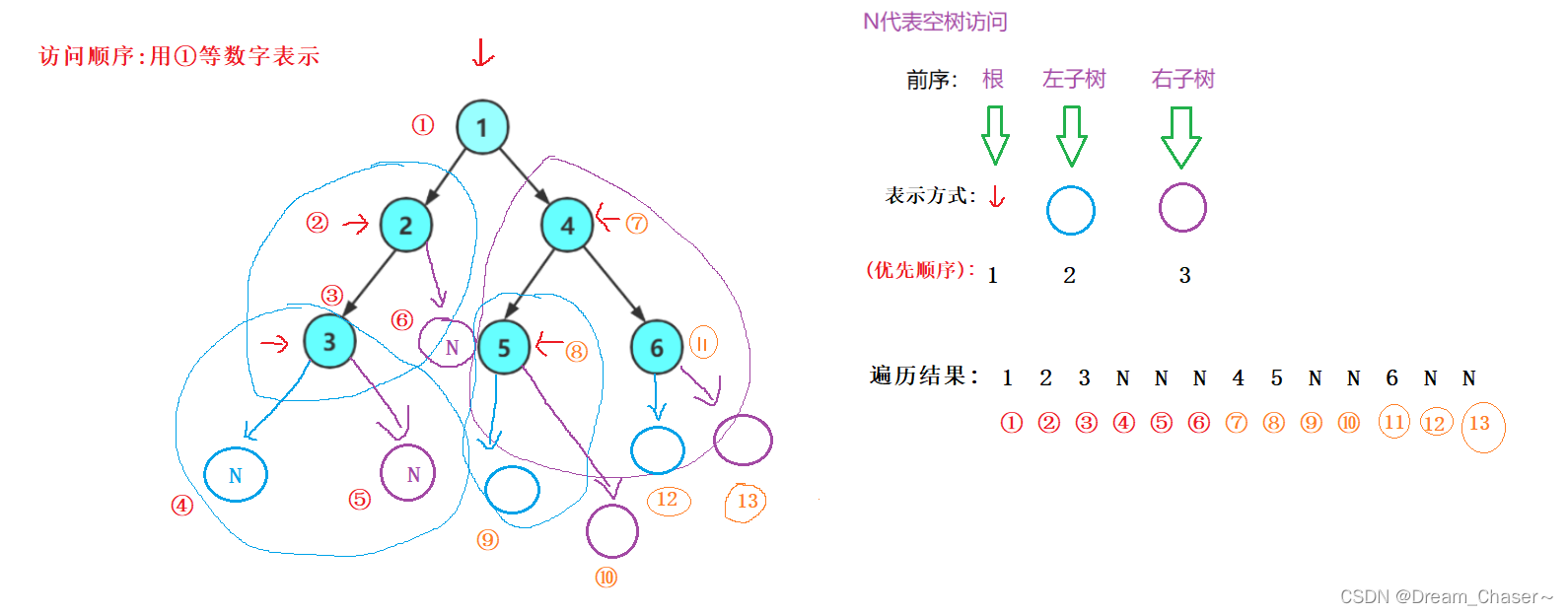
注意:上述代码并不是创建二叉树的方式,真正创建二叉树方式后序详解重点讲解。再看二叉树基本操作前,再回顾下二叉树的概念, 二叉树是:1. 空树2. 非空:根节点,根节点的左子树、根节点的右子树组成的。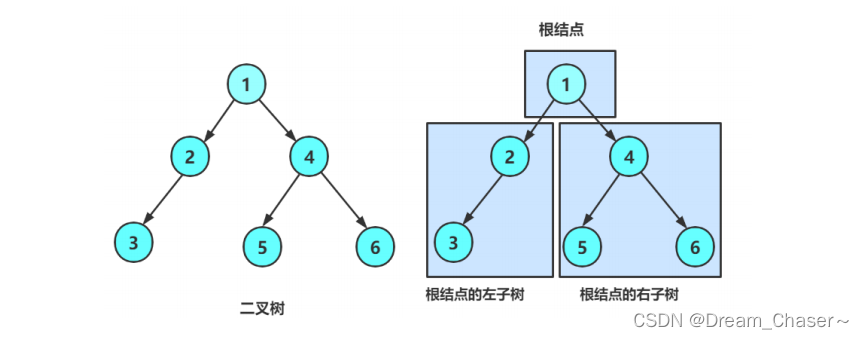
后续遍历(Postorder Traversal)
访问根结点的操作发生在遍历其左右子树之后. 由于被访问的结点必是某子树的根, 所以N(Node)、L(Left subtree)和R(Right subtree)又可解释为根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历
由于被访问的结点必是某子树的根, 所以N(Node)、L(Left subtree)和R(Right subtree)又可解释为根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历层序遍历(LevelOrder)
层序遍历 : 除了先序遍历、中序遍历、后序遍历外,还可以对二叉树进行层序遍历。设二叉树的根节点所在层数为1,层序遍历就是从所在二叉树的根节点出发,首先访问第一层的树根节点,然后从左到右访问第2层上的节点,接着是第三层的节点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。
2.3二叉树功能的实现
二叉树结构定义(struct BinaryTreeNode)
代码实现:
- typedef int BTDataType;
- typedef struct BinaryTreeNode
- {
- BTDataType data;
- struct BinaryTreeNode* left;
- struct BinaryTreeNode* right;
- }BTNode;
二叉树节点的创建(CreatBinaryTree)
- BTNode* BuyNode(BTDataType x)//树中一个节点的创建
- {
- BTNode* node = (BTNode*)malloc(sizeof(BTNode));
- if (node == NULL)
- {
- perror("malloc fail");
- return NULL;
- }
- node->data = x;
- node->left = NULL;
- node->right = NULL;
- return node;
- }
- BTNode* CreatBinaryTree()//树的构造
- {
- BTNode* node1 = BuyNode(1);
- BTNode* node2 = BuyNode(2);
- BTNode* node3 = BuyNode(3);
- BTNode* node4 = BuyNode(4);
- BTNode* node5 = BuyNode(5);
- BTNode* node6 = BuyNode(6);
- node1->left = node2;
- node1->right = node4;
- node2->left = node3;
- node4->left = node5;
- node4->right = node6;
- return node1;
- }
二叉树的前序遍历函数(PrevOrder)
递归不可能一直调用函数,因为这个过程一直在创建栈帧,即使栈再大,也会栈溢出。所以肯定会回归,回归的本质就是销毁栈帧。
递归是由两个部分构成:
1.子问题
2.返回条件
图解:


代码实现:
- void PrevOrder(BTNode* root)
- {
- if (root == NULL)
- {
- printf("N ");
- return;
- }
- printf("%d ", root->data);
- PrevOrder(root->left);
- PrevOrder(root->right);
- }
二叉树的中序遍历函数(InOrder)
绘图:

- void InOrder(BTNode* root)
- {
- if (root == NULL)
- {
- printf("N ");
- return;
- }
- InOrder(root->left);
- printf("%d ", root->data);
- InOrder(root->right);
- }
二叉树的后序遍历函数(PostOrder)
跟前中序的思路相差不大,这里就不绘图了。
代码实现:
- void PostOrder(BTNode* root)
- {
- if (root == NULL)
- {
- printf("N ");
- return;
- }
- PostOrder(root->left);
- PostOrder(root->right);
- printf("%d ", root->data);
- }
统计二叉树节点个数(BTreeSize)
画出递归展开图:
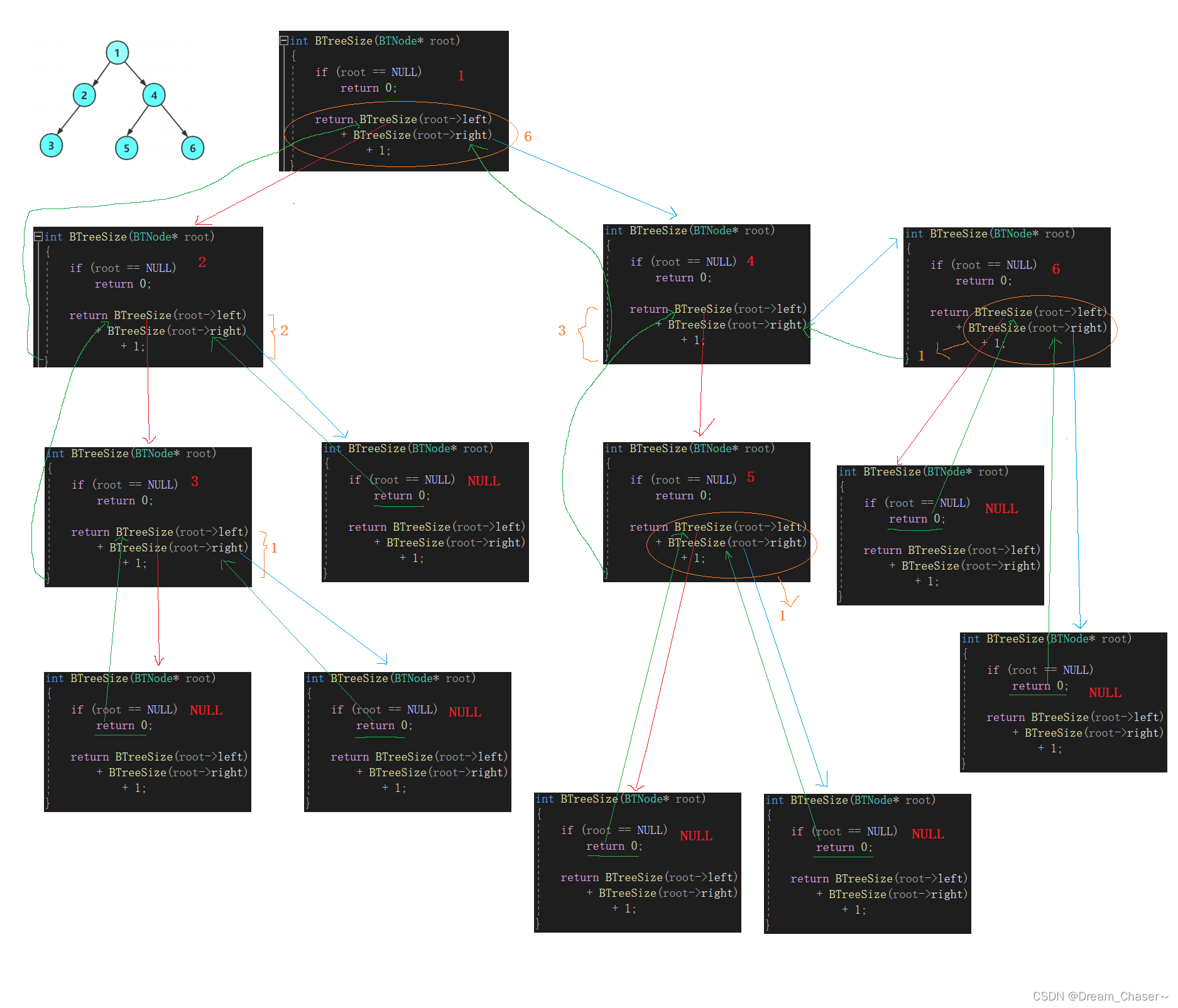
- int BTreeSize(BTNode* root)
- {
- //写法一
- if (root == NULL)
- return 0;
- return BTreeSize(root->left) + BTreeSize(root->right) + 1;
- //写法二
- return root == NULL ? 0 : BTreeSize(root->left) + BTreeSize(root->right) + 1;
- }
求出叶子节点的数量(BTreeLeafSize)
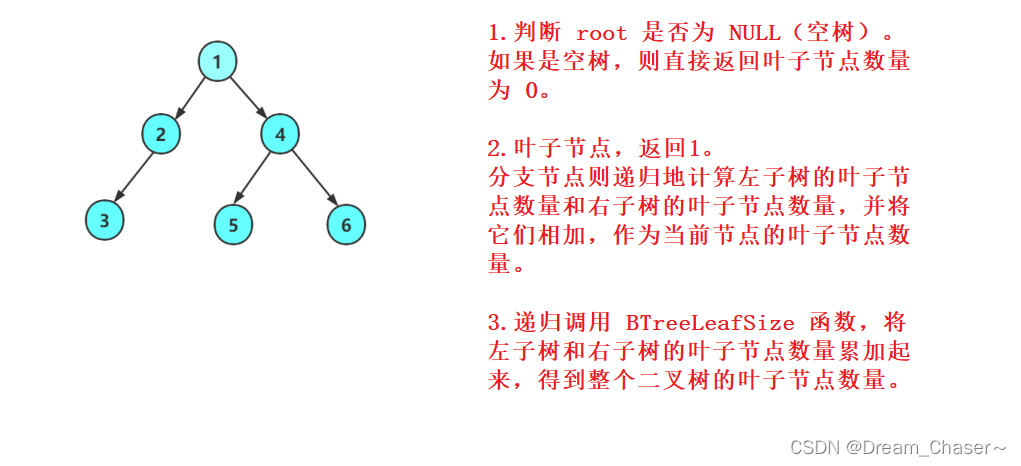
进入函数首先判断根节点是否为空,为空就直接返回0,说明树为空,直接返回叶子节点数量为0。
接下来,检查当前的节点是叶子节点还是分支节点,若代码检查当前节点是否为叶子节点,即该节点的左子节点和右子节点都为空。如果是叶子节点,返回叶子节点数量为1。
如果当前节点为分支节点,则继续调用该函数,计算左子树和右子树的叶子节点数量,并将它们相加,得到当前节点为根的子树的叶子节点数量。
最后,函数返回左子树和右子树叶子节点数量的和,即整个二叉树的叶子节点数量。
- int BTreeLeafSize(BTNode* root)//接受一个指向二叉树节点的指针root作为参数
- {
- if (root == NULL)//代码检查根节点是否为空
- {
- return 0;
- }
- if ( root->left==NULL &&root->right==NULL)
- {
- return 1;
- }
- return BTreeLeafSize(root->left) + BTreeLeafSize(root->right);
- }
求二叉树的高度(BTreeHeight)
先比较一下以下的哪种代码更优:
方案一:
在递归调用
BTreeHeight函数之后,并没有对返回值进行保存和比较,而是直接返回了当前节点的左子树和右子树的高度中较大的一个加1。这样的实现虽然能够得到正确的结果,但是效率较低。因为在计算左子树的高度和右子树的高度时,每次都会重复递归调用BTreeHeight函数- int BTreeHeight(BTNode* root)
- {
- if (root == NULL)
- {
- return 0;
- }
- return BTreeHeight(root->left) > BTreeHeight(root->right) ?
- BTreeHeight(root->left) + 1 : BTreeHeight(root->right) + 1;
- }
为了更好地理解方案一的解释,这里写出一个不用三目运算符,但是等价于上述代码的代码
画图理解:
这里其实用到的是分治算法,通常分为三个步骤:
-
分解(Divide):将原问题划分为若干个规模较小的子问题。这一步通常在递归的过程中进行,直到问题足够简单,可以直接求解。
-
解决(Conquer):递归地解决子问题。对于每个子问题,如果它的规模足够小,可以直接求解;否则,继续递归地将子问题划分为更小的子问题。
-
合并(Combine):将子问题的解合并得到原问题的解。这一步通常在递归的回溯过程中进行。

代码实现:
- int BTreeHeight(BTNode* root)
- {
- if (root == NULL)
- {
- return 0;
- }
- int h = 0;
- if (BTreeHeight(root->left) > BTreeHeight(root->right))
- {
- h = BTreeHeight(root->left) + 1;
- }
- else
- {
- h = BTreeHeight(root->right) + 1;
- }
- return h;
- }
力扣执行:

方案二:

使用了两个变量
leftHeight和rightHeight分别保存了左子树和右子树的高度。通过递归调用BTreeHeight函数分别计算左子树和右子树的高度,并将结果保存在这两个变量中。然后比较leftHeight和rightHeight的值,将较大值加1作为当前节点的高度返回。这样的实现避免了重复计算,提高了效率。- int BTreeHeight(BTNode* root)
- {
- if (root == NULL)
- {
- return 0;
- }
- int leftHeight = BTreeHeight(root->left);
- int rightHeight = BTreeHeight(root->right);
- return leftHeight > rightHeight ? leftHeight + 1 : rightHeight+ 1;
- }
力扣执行:

二叉树第k层节点个数(BTreeLevelKSize)
子问题:
转换成左子树的第k-1层和右子树的右子树的第k-1层
结束条件:
- k == 1且节点不为空
- 节点为空

代码实现:
- int BTreeLevelKSize(BTNode* root, int k)
- {
- assert(k > 0);
- if (root == NULL)
- return 0;
- if (k == 1)
- return 1;
- return BTreeLevelKSize(root->left, k - 1)
- + BTreeLevelKSize(root->right, k - 1);
- }
二叉树查找值为x的节点(BTreeFind)
思路:就如果根节点为空,直接返回NULL,如果找到了就返回x这个节点的地址。
从根节点开始遍历,先从左子树开始找,继续循环上述思路,如果节点不为NULL,但是节点不为x,那也是返回NULL,注意这个NULL是返回上一层的,谁调用它就返回给此函数。之后找右子树,也是一样的思路。
左子树整体找完之后,从右子树整体开始找,重复上述过程。特别强调一个点,return返回的时候不会return到最外层,一定是逐层逐层返回的,没有跳跃的一个过程。
画出递归展开图:

代码实现:
- BTNode* BTreeFind(BTNode* root,BTDataType x)
- {
- if (root == NULL)
- return NULL;
- if (root->data == x)
- return root;
- int ret1 = BTreeFind(root->left, x);
- if (ret1)
- return ret1;
- int ret2 = BTreeFind(root->right, x);
- if (ret2)
- return ret2;
- return NULL;
- }
二叉树的层序遍历(LevelOrder)
层序遍历是用队列实现的,所以要使用队列的结构体,以下的结构体都要用到
- typedef struct BTNode* QDataType;//注意这个地方的类型
- typedef struct QueueNode
- {
- QDataType data;
- struct QueueNode* next;
- }QNode;
- typedef struct Queue
- {
- QNode* phead;
- QNode* ptail;
- int size;
- }Queue;//表示队列整体,一个是出数据,一个是入数据.
- typedef int BTDataType;
- typedef struct BinaryTreeNode
- {
- BTDataType data;
- struct BinaryTreeNode* left;
- struct BinaryTreeNode* right;
- }BTNode;
画处解析图:
队列:先进先出
核心思路:上一层出时带下一层进队列
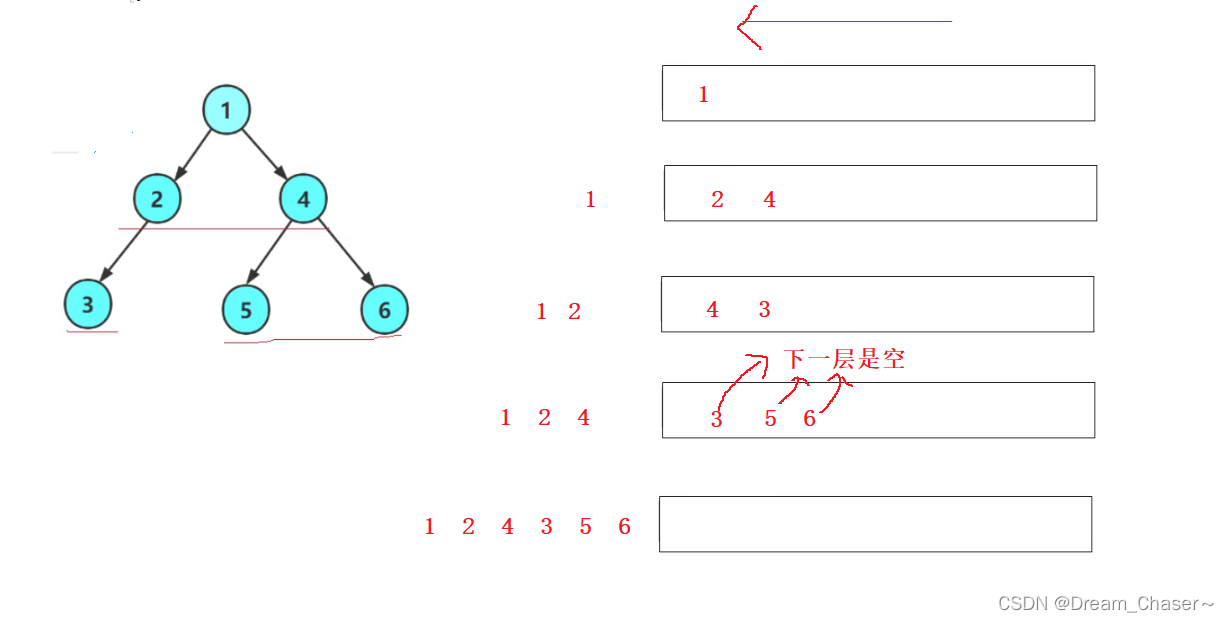
解析: 其实就是由原来的队列里面data的int类型,变成了struct BTreeNode* 类型的指针,指向了这个数节点。

代码实现:
- void LevelOrder(BTNode* root)
- {
- Queue q;//在函数内部,定义了一个队列q,并通过调用QueueInit函数对队列进行初始化。
- QueueInit(&q);
- //如果根节点root不为空,将根节点入队,即调用QueuePush函数将root指针插入到队列q中。
- if (root)
- QueuePush(&q,root);
- while (!QueueEmpty(&q))
- {
- BTNode* front = QueueFront(&q);//首先通过调用QueueFront函数获取队列q的队首元素,并将其赋值给指针变量front
- QueuePop(&q);//调用QueuePop函数将队首元素出队
- printf("%d ", front->data);//通过printf函数打印front指向的节点的数据值
- //如果front的左子节点不为空,将左子节点入队,
- //即调用QueuePush函数将front->left指针插入到队列q中
- if (front->left)
- QueuePush(&q, front->left);//后面这个参数是一个值,不是地址
- //如果front的右子节点不为空,将右子节点入队,
- //即调用QueuePush函数将front->right指针插入到队列q中。
- if (front->right)
- QueuePush(&q, front->right);//后面这个参数是一个值,不是地址
- //循环体内的操作完成后,继续下一次循环,直到队列q为空。
- }
- //最后,打印换行符表示层序遍历结束,
- //并调用QueueDestroy函数销毁队列q,释放内存。
- printf("\n");
- QueueDestroy(&q);
- }
二叉树的销毁(BTDestroy)
解析:要先判断根节点本身是否为空,为空就不销毁,返回。
销毁是用到后序遍历的,因为中途删掉了根节点,那么左右指针就找不到了,所以后序遍历适合实现二叉树的销毁。
画图:

- void BTDestroy(BTNode* root)
- {
- if (root == NULL)
- {
- return NULL;
- }
- BTDestroy(root->left);
- BTDestroy(root->right);
- free(root);
- }
判断一棵树是否为完全二叉树(BinaryTreeComplete)
非完全二叉树

完全二叉树
思路一样的就不画动图了,只要前面遇到一次空,立即跳出循环,停止插入元素,然后检查后面的元素是否为空,后面全是空就是完全二叉树了。
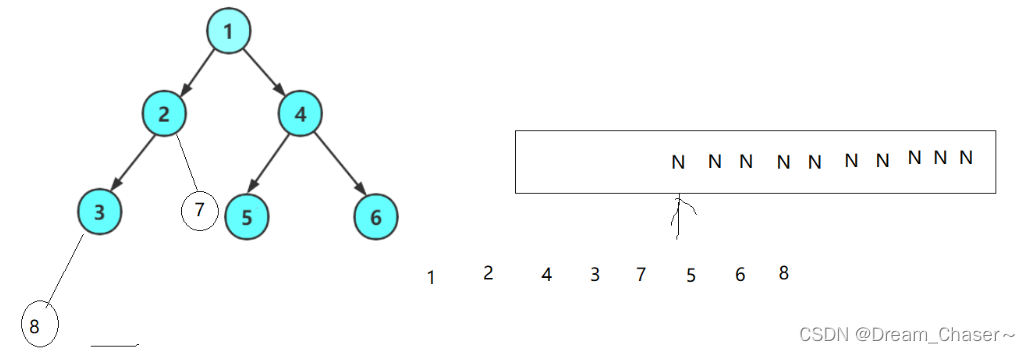
以下这个二叉树就不是完全二叉树了
代码实现:
- bool BTreeComplete(BTNode* root)
- {
- Queue q;
- QueueInit(&q);
- if (root)
- QueuePush(&q,root);
- while (!QueueEmpty(&q))//遍历树直到找到第一个空节点
- {
- BTNode* front= QueueFront(&q);
- QueuePop(&q);
- //遇到空就跳出
- if (front == NULL)
- {
- break;
- }
- QueuePush(&q, front->left);
- QueuePush(&q, front->right);
- }
- // 检查后面的节点有没有非空
- // 有非空,不是完全二叉树
- while (!QueueEmpty(&q))//由于中途遇到空,所以跳出循环,这次循环是为了检查后面元素是否为空
- {
- BTNode* front = QueueFront(&q);
- QueuePop(&q);
- if (front)
- {
- QueueDestroy(&q);
- return false;
- }
- }
- QueueDestroy(&q);
- return true;
- }
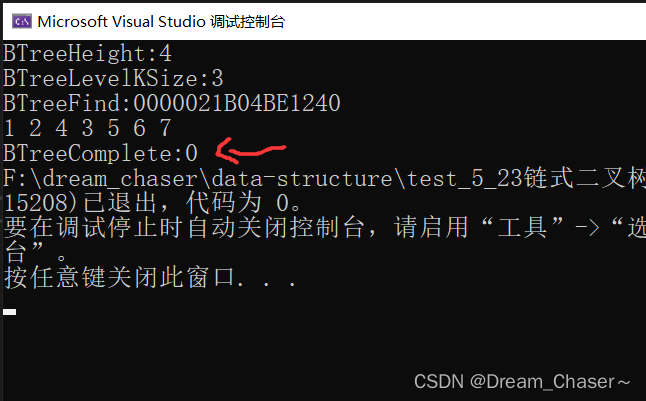
执行:
本篇到此结束,感谢来访!
-
相关阅读:
Flink--9、双流联结(窗口联结、间隔联结)
【Python】Pycharm中设置使用conda的虚拟环境(保姆级图文)
植物大战僵尸杂交版破解C++实现
Linux系统安装MongoDB流程
Nginx
SpringBoot 统一功能处理
ESP32 下蓝牙播放音乐
Promise笔记
php中识别url被篡改并阻止访问的实现方式是什么
第三章 搜索与图论(二)
- 原文地址:https://blog.csdn.net/weixin_65186652/article/details/133894482