-
模式识别——高斯分类器
模式识别——高斯分类器
需知
所有问题定义在分类问题下,基于贝叶斯决策
定义
条件概率为多元高斯分布,此时观测为向量 X = X 1 , X 2 , . . . , X n X={X_1,X_2,...,X_n} X=X1,X2,...,Xn,通过极大后验展开可以得到最优决策函数:

决策函数可以写为:

d d d就是马氏距离,代表两个高斯分布之间的距离。而 α \alpha α则代表了类别的先验。特殊情况(方差一致)
方差一致的话分类器就是线性的。



Sigmoid
使用原始的BDR定义可以推导出,每个类别的概率概率为sigmoid函数(原始定义考虑观测的边缘概率,所以计算的就是概率(概率和为1),所以为sigmoid函数。而在决策时不考虑边缘概率,约掉了归一化参数,其实两者的判决边界仍然是相同的)


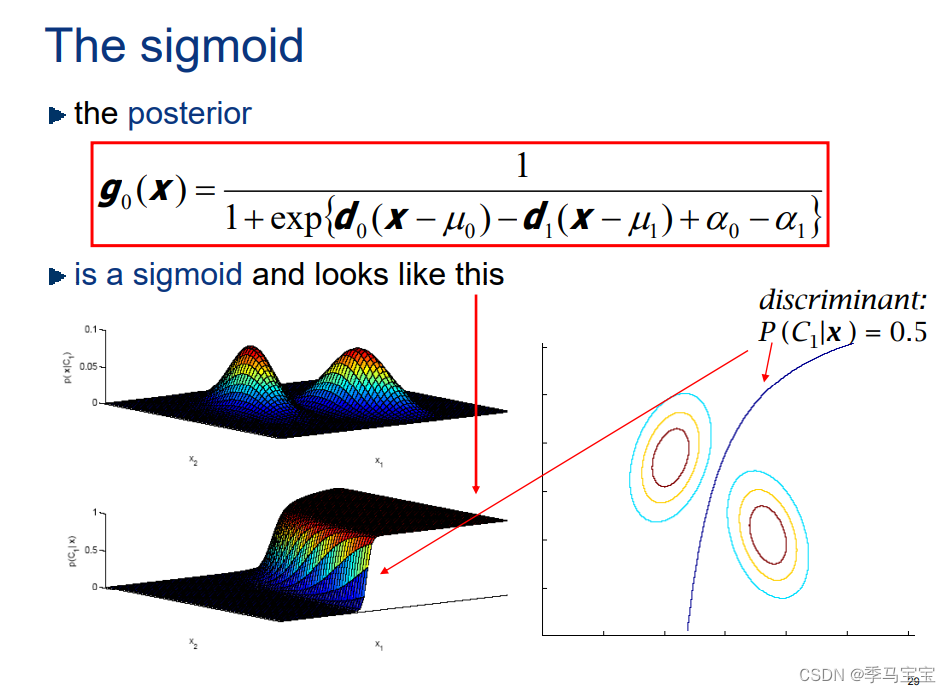
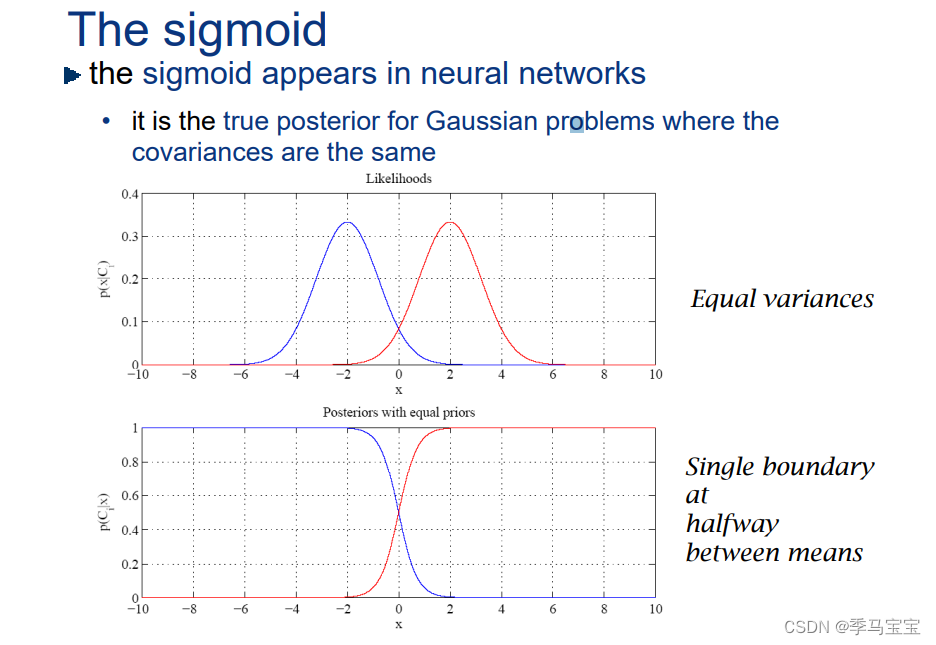
协方差一致有唯一分界线:
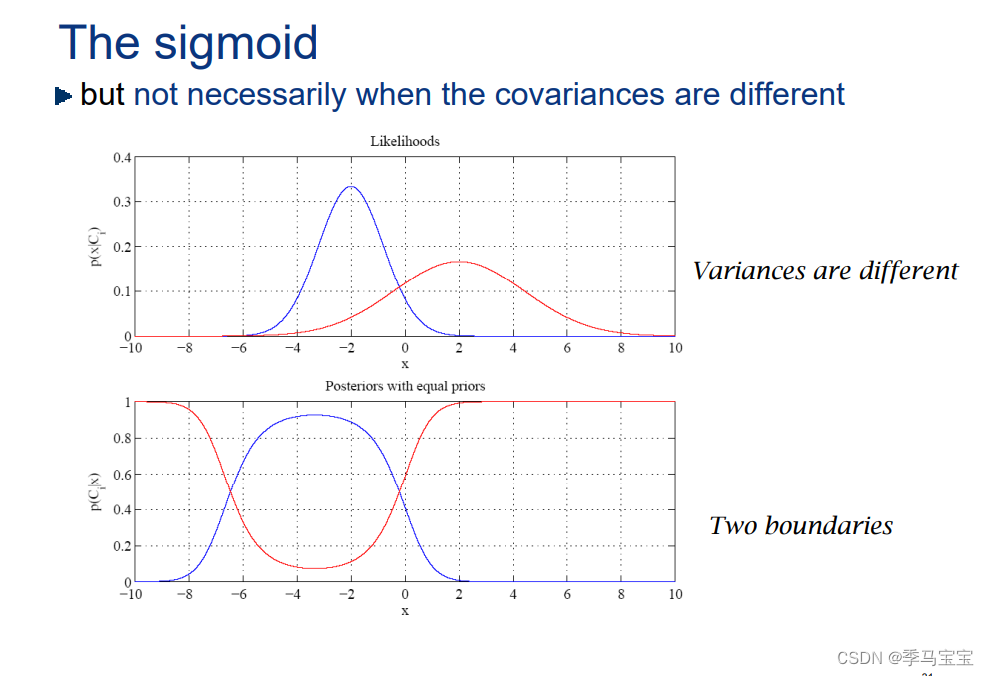
协方差不一致有两个分界线:
-
相关阅读:
tBERT-BERT融合主题模型
【论文阅读】MixMatch: A Holistic Approach to Semi-Supervised Learning
NodeJS @kubernetes/client-node连接到kubernetes集群的方法
使用 Java 操作 Redis
使用knuth Durstenfeld Shuffle置乱关键区域
Qt QtWidgets相关问题汇总
Windows端口号被占用的查看方法及解决办法
vue补充继上一篇
#FreeRTOS延时函数
python基于django的商品比价平台
- 原文地址:https://blog.csdn.net/qq_21043585/article/details/133992788