-
【Matlab】三维绘图函数汇总
本文用于汇总 Matlab 中的三维绘图函数。plot3() 函数用于绘制用参数方程表示的三维曲线。ezplot3() 函数用于三维曲线的符号绘图,需要用参数方程表示。mesh() 函数用于绘制三维曲面网格。surf() 函数用于绘制三维空间曲面。
目录
1. plot3()
plot3() 函数用于绘制三维曲线,需要用参数方程表示,plot3() 的用法与 plot() 函数类似。以下是 Matlab 关于 plot3() 函数的语法说明。
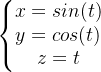
plot3(X,Y,Z) 绘制三维空间中的坐标。
-
要绘制由线段连接的一组坐标,请将
X、Y、Z指定为相同长度的向量。 -
要在同一组坐标轴上绘制多组坐标,请将
X、Y或Z中的至少一个指定为矩阵,其他指定为向量。
示例:绘制三维螺旋图
将
t定义为由介于 0 和 10π 之间的值组成的向量。将st和ct定义为正弦和余弦值向量。然后绘制曲线。- t = 0:pi/50:10*pi;
- st = sin(t);
- ct = cos(t);
- plot3(st,ct,t)

2. ezplot3()
ezplot3() 函数用于三维曲线的符号绘图,需要用参数方程表示。以下是 Matlab 关于 ezplot3() 函数的语法说明。

ezplot3(funx,funy,funz)
在默认域 0 <
t< 2π 中绘制空间曲线funx(t)、funy(t)和funz(t)。funx、funy和funz可以是函数句柄、字符向量或字符串。示例:绘制参数曲线
在 [0,6π] 区间上绘制此参数化曲线。
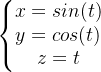
ezplot3('sin(t)','cos(t)','t',[0,6*pi])
3. mesh()
mesh() 函数用于绘制三维曲面网格,网格上的点由 X,Y,Z 三个矩阵给出。以下是 Matlab 关于 mesh() 的用法说明。

mesh(X,Y,Z)
创建一个网格图,该网格图为三维曲面,有实色边颜色,无面颜色。该函数将矩阵
Z中的值绘制为由X和Y定义的 x-y 平面中的网格上方的高度。边颜色因Z指定的高度而异。示例:绘制墨西哥帽子。
由函数
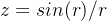 确定的曲面,其中
确定的曲面,其中 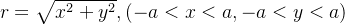 。
。- [X,Y] = meshgrid(-8:.5:8);
- R = sqrt(X.^2 + Y.^2) + eps;
- Z = sin(R)./R;
- mesh(X,Y,Z)

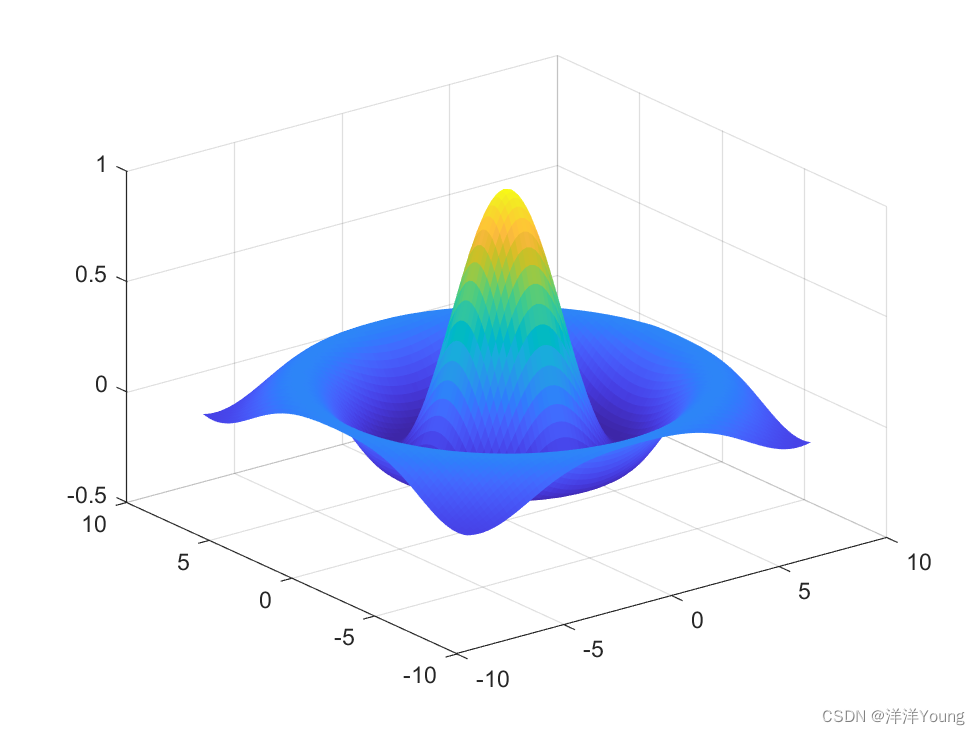
4. surf()
surf() 函数用于绘制三维空间曲面,曲面上的点由 X,Y,Z 三个矩阵给出。以下是 Matlab 关于 surf() 的用法说明。

surf(X,Y,Z)
创建一个三维曲面图,它是一个具有实色边和实色面的三维曲面。该函数将矩阵
Z中的值绘制为由X和Y定义的 x-y 平面中的网格上方的高度。曲面的颜色根据Z指定的高度而变化。- [X,Y] = meshgrid(-8:.2:8);
- R = sqrt(X.^2 + Y.^2) + eps;
- Z = sin(R)./R;
- surf(X,Y,Z)
- shading flat
-
-
相关阅读:
3.5 讲一讲关于小红书的搜索引流技巧【玩赚小红书】
每日一题 LCP 06. 拿硬币
Java web中使用servlet进行用户登录
SwiftUI调用相机拍照
【人工智能 | 认知观与系统类别】从宏观角度看人工智能认知观与系统类别:探索人工智能无垠领域
基于显扬科技自主研发3D机器视觉HY-M5在物流行业包裹分拣中的应用
Sass样式使用集锦
常见的通用型项目管理软件推荐
爱尔眼科眼底病论坛糖网病变智能(AI)监测防治培训举办!
2311vim极语言加高亮
- 原文地址:https://blog.csdn.net/sxyang2018/article/details/133978315