【换根DP】CF1882 D

Problem - D - Codeforces

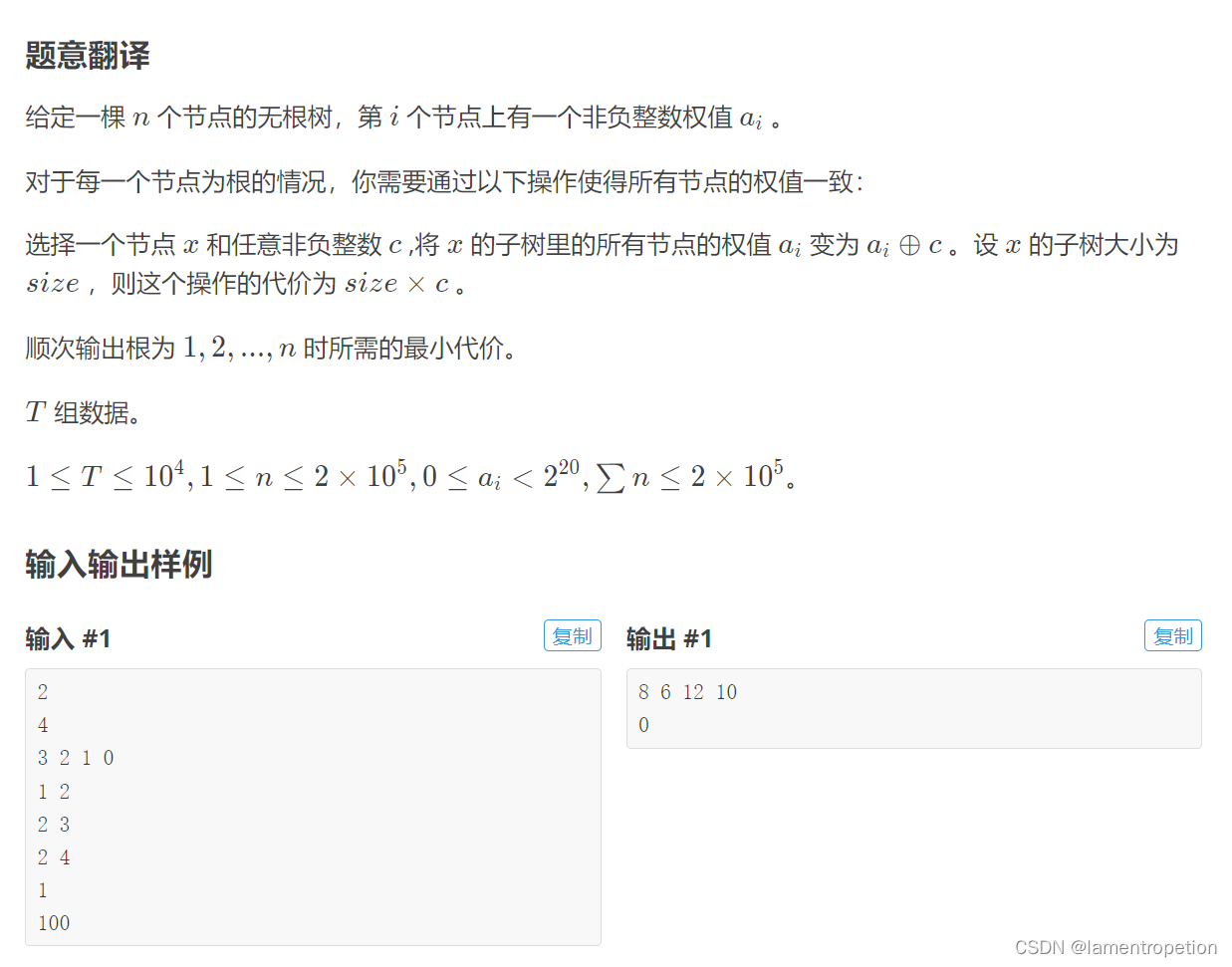
思路：

一个很套路的换根

首先观察到，先对儿子一定比先对父亲操作来的代价小，因此考虑先对儿子操作，再对父亲操作

然后就可以直接换根了，首先考虑树形DP，设dp[u] 为 把 u 子树染成同一种颜色的最小代价

那么根据刚刚的先操作儿子，转移方程为

dp[u] += dp[v] + (a[u] ^ a[v]) * sz[v]

然后换根就正常换就好了

Code：

#include 
 
#define int long long
 
constexpr int N = 2e5 + 10;
constexpr int mod = 998244353;
 
std::vector<int> adj[N];
 
int n;
int a[N];
int dp[N], sz[N];
 
void dfs1(int u, int fa) {
	sz[u] = 1;
	for (auto v : adj[u]) {
		if (v == fa) continue;
		dfs1(v, u);
		sz[u] += sz[v];
		dp[u] += dp[v] + (a[u] ^ a[v]) * sz[v];
	}
}
void dfs2(int u, int fa) {
	for (auto v : adj[u]) {
		if (v == fa) continue;
		dp[u] -= (a[u] ^ a[v]) * sz[v] + dp[v];
		sz[u] -= sz[v];
		int t1 = (a[u] ^ a[v]) * sz[v] + dp[v];
		int t2 = sz[v];
		dp[v] += (a[v] ^ a[u]) * sz[u] + dp[u];
		sz[v] += sz[u];
		dfs2(v, u);
		dp[u] += t1;
		sz[u] += t2;
	}
}
void solve() {
	std::cin >> n;
	for (int i = 1; i <= n; i ++) {
		adj[i].clear();
		dp[i] = sz[i] = 0;
	}
	for (int i = 1; i <= n; i ++) {
		std::cin >> a[i];
	}
	for (int i = 1; i <= n - 1; i ++) {
		int u, v;
		std::cin >> u >> v;
		adj[u].push_back(v);
		adj[v].push_back(u);
	}
	dfs1(1, 0);
	dfs2(1, 0);
	for (int i = 1; i <= n; i ++) {
		std::cout << dp[i] << " \n" [i == n];
	}
}
signed main() {
	std::ios::sync_with_stdio(false);
	std::cin.tie(nullptr);
 
	int t = 1;
	std::cin >> t;
	while (t--) {
		solve();
	}
	return 0;
}