LeetCode_并查集_DFS_中等_2316.统计无向图中无法互相到达点对数

1.题目

给你一个整数 n ，表示一张 无向图 中有 n 个节点，编号为 0 到 n - 1 。同时给你一个二维整数数组 edges ，其中 edges[i] = [a_i, b_i] 表示节点 a_i 和 b_i 之间有一条无向边。请你返回无法互相到达的不同点对数目。

示例 1：

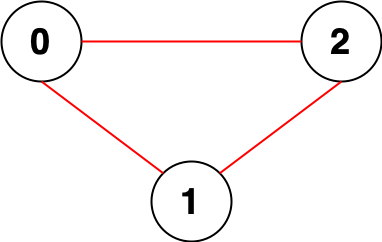
输入：n = 3, edges = [[0,1],[0,2],[1,2]]
输出：0
解释：所有点都能互相到达，意味着没有点对无法互相到达，所以我们返回 0。

示例 2：

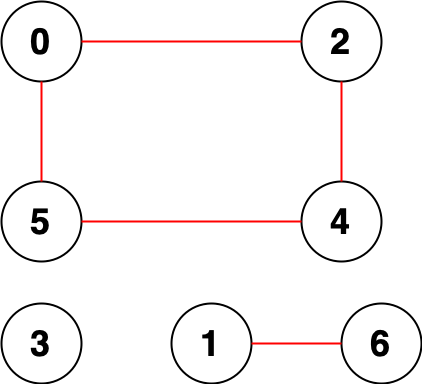
输入：n = 7, edges = [[0,2],[0,5],[2,4],[1,6],[5,4]]
输出：14
解释：总共有 14 个点对互相无法到达：
[[0,1],[0,3],[0,6],[1,2],[1,3],[1,4],[1,5],[2,3],[2,6],[3,4],[3,5],[3,6],[4,6],[5,6]]
所以我们返回 14。

提示：
1 <= n <= 10⁵
0 <= edges.length <= 2 * 10⁵
edges[i].length == 2
0 <= a_i, b_i < n
a_i != b_i
不会有重复边。

2.思路

（1）并查集

（2）DFS

3.代码实现（Java）

//思路1————并查集
class Solution {
    public long countPairs(int n, int[][] edges) {
        UnionFind uf = new UnionFind(n);
        for (int[] edge : edges) {
            uf.union(edge[0], edge[1]);
        }
        long res = 0;
        for (int i = 0; i < n; i++) {
            res += n - uf.getSize(uf.find(i));
        }
        return res / 2;
    }
}

class UnionFind {
    // parent[x] 表示节点 x 的父节点
    int[] parent;
    // sizes[x] 表示根节点 x 所在的树的顶点总数
    int[] sizes;

    public UnionFind(int n) {
        parent = new int[n];
        for (int i = 0; i < n; i++) {
            parent[i] = i;
        }
        sizes = new int[n];
        Arrays.fill(sizes, 1);
    }

    public int find(int x) {
        if (parent[x] != x) {
            parent[x] = find(parent[x]);
        }
        return parent[x];
    }

    public void union(int x, int y) {
        int rootX = find(x);
        int rootY = find(y);
        if (rootX != rootY) {
            if (sizes[rootX] > sizes[rootY]) {
                parent[rootY] = rootX;
                sizes[rootX] += sizes[rootY];
            } else {
                parent[rootX] = rootY;
                sizes[rootY] += sizes[rootX];
            }
        }
    }

    public int getSize(int x) {
        return sizes[x];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55

//思路2————DFS
class Solution {

    List<Integer>[] graph;
    boolean[] visited;

    public long countPairs(int n, int[][] edges) {
        graph = buildGraph(n, edges);
        visited = new boolean[n];
        long res = 0;
        for (int i = 0; i < n; i++) {
            if (!visited[i]) {
                long cnt = dfs(i);
                res += cnt * (n - cnt);
            }
        }
        return res / 2;
    }

    //通过 DFS 计算当前顶点 u 所在的连通分量的顶点数
    public long dfs(int u) {
        visited[u] = true;
        int cnt = 1;
        for (int v : graph[u]) {
            if (!visited[v]) {
                cnt += dfs(v);
            }
        }
        return cnt;
    }

    //构造邻接表
    public List<Integer>[] buildGraph(int n, int[][] edges) {
        List<Integer>[] graph = new ArrayList[n];
        for (int i = 0; i < n; i++) {
            graph[i] = new ArrayList<>();
        }
        for (int[] edge : edges) {
            int u = edge[0];
            int v = edge[1];
            graph[u].add(v);
            graph[v].add(u);
        }
        return graph;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46