LC-2316. 统计无向图中无法互相到达点对数（DFS、并查集）

2316. 统计无向图中无法互相到达点对数

中等

给你一个整数 n ，表示一张 无向图 中有 n 个节点，编号为 0 到 n - 1 。同时给你一个二维整数数组 edges ，其中 edges[i] = [ai, bi] 表示节点 ai 和 bi 之间有一条 无向 边。

请你返回 无法互相到达 的不同 点对数目 。

示例 1：

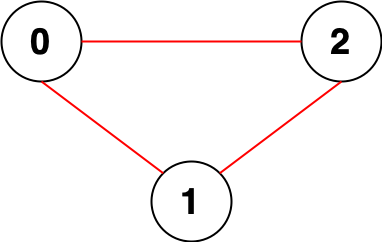
输入：n = 3, edges = [[0,1],[0,2],[1,2]]
输出：0
解释：所有点都能互相到达，意味着没有点对无法互相到达，所以我们返回 0 。
1
2
3

示例 2：

输入：n = 7, edges = [[0,2],[0,5],[2,4],[1,6],[5,4]]
输出：14
解释：总共有 14 个点对互相无法到达：
[[0,1],[0,3],[0,6],[1,2],[1,3],[1,4],[1,5],[2,3],[2,6],[3,4],[3,5],[3,6],[4,6],[5,6]]
所以我们返回 14 。
1
2
3
4
5

提示：

• 1 <= n <= 105
• 0 <= edges.length <= 2 * 105
• edges[i].length == 2
• 0 <= ai, bi < n
• ai != bi
• 不会有重复边。

DFS

class Solution {
    // 统计联通分量 个数 和 大小
    // 然后递推，求出点对个数
    // 例如 4 1 2
    // 4 * 1 + 5 * 2
    public long countPairs(int n, int[][] edges) {
        List<Integer>[] g = new ArrayList[n];
        Arrays.setAll(g, e -> new ArrayList<>());
        for(int[] e : edges){
            int x = e[0], y = e[1];
            g[x].add(y);
            g[y].add(x);
        }
        boolean[] vis = new boolean[n];
        List<Integer> list = new ArrayList<>();
        for(int i = 0; i < n; i++){
            if(!vis[i]){
                int cnt = dfs(i, -1, g, vis);
                list.add(cnt);
            }
        }
        long res = 0l, sum = 0l;
        for(Integer e : list){
            res += e * sum;
            sum += e;
        }
        return res;
    }

    private int dfs(int x, int fa, List<Integer>[] g, boolean[] vis){
        int res = 1;
        vis[x] = true;
        for(int y : g[x]){
            if(y != fa && !vis[y])
                res += dfs(y, x, g, vis);
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

并查集

统计连通块大小可以用并查集做

class Solution {
    // 统计联通分量 个数 和 大小
    public long countPairs(int n, int[][] edges) {
        UF uf = new UF(n);
        for(int[] e : edges){
            uf.union(Math.max(e[0], e[1]), Math.min(e[0], e[1]));
        }
        Map<Integer, Integer> map = new HashMap<>();
        for(int i = 0; i < n; i++){
            map.merge(uf.find(i), 1, Integer::sum);
        }
        long res = 0l, sum = 0l;
        for(int x : map.keySet()){
            res += (long)map.get(x) * sum;
            sum += map.get(x);
        }
        return res;
    }
}

/* ------------ 并查集模版 ------------ */
class UF {
    int[] parent; // par数组用来存储根节点，par[x]=y表示x的根节点为y
    int[] size; // size[i]表示以i为根的联通块大小
    int count; // count表示连通块个数，每次调用union时count-1
    
    public UF(int n) {
        this.count = n;
        parent = new int[n];
        size = new int[n];
        for (int i = 0; i < n; i++) {
            parent[i] = i;
            size[i] = 1;
        }
    }
    
    public void union(int x, int y) {
        int rootx = find(x);
        int rooty = find(y);
        if (rootx == rooty) return;
        else//不是同一个根，即不在同一个集合，就合并
            parent[rootx] = rooty;
            size[rooty] += size[rootx];
        count--;
    }
    
    public int find(int x) {
        // 路径压缩
        if (parent[x] != x) {
            parent[x] = find(parent[x]);
        }
        return parent[x];
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55