聚类方法总结及code

参考链接

聚类方法的分类：

10类常用方法解析：
1.亲和力传播

1）概述
AP算法的基本思想是将全部数据点都当作潜在的聚类中心(称之为exemplar)，然后数据点两两之间连线构成一个网络(相似度矩阵)，再通过网络中各条边的消息(responsibility:吸引度和availability:归属度)传递计算出各样本的聚类中心。
1）相似度： 点j作为点i的聚类中心的能力，记为S(i,j)。一般使用负的欧式距离，所以S(i,j)越大，表示两个点距离越近，相似度也就越高。使用负的欧式距离，相似度是对称的，如果采用其他算法，相似度可能就不是对称的。
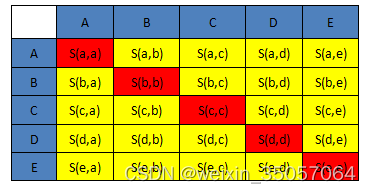
2）相似度矩阵：N个点之间两两计算相似度，这些相似度就组成了相似度矩阵。如图1所示的黄色区域，就是一个5*5的相似度矩阵(N=5)
3) preference：指点i作为聚类中心的参考度(不能为0)，取值为S对角线的值(图1红色标注部分)，此值越大，最为聚类中心的可能性就越大。但是对角线的值为0，所以需要重新设置对角线的值，既可以根据实际情况设置不同的值，也可以设置成同一值。一般设置为S相似度值的中值。(有的说设置成S的最小值产生的聚类最少，但是在下面的算法中设置成中值产生的聚类是最少的)
4）Responsibility(吸引度):指点k适合作为数据点i的聚类中心的程度，记为r(i,k)。如图2红色箭头所示，表示点i给点k发送信息，是一个点i选点k的过程。
5）Availability(归属度):指点i选择点k作为其聚类中心的适合程度，记为a(i,k)。如图3红色箭头所示，表示点k给点i发送信息，是一个点k选diani的过程。
6）exemplar：指的是聚类中心。
7）r (i, k)加a (i, k)越大,则k点作为聚类中心的可能性就越大,并且i点隶属于以k点为聚类中心的聚类的可能性也越大

2）算法步骤
a）计算相似度矩阵，并且设置参考度，这里使用相似度矩阵的中值
b）计算吸引度矩阵，即R值。
c）计算归属度矩阵，即A值
d）迭代更新R值和A值。终止条件是聚类中心在一定程度上不再更新或者达到最大迭代次数
e）根据求出的聚类中心，对数据进行分类
这个步骤产生的是一个归类列表，列表中的每个数字对应着样本数据中对应位置的数据的分类

3）图解过程

4）算法函数
a）sklearn.cluster.AffinityPropagation

b）主要参数(详细参数)
damping : 阻尼系数，取值[0.5,1)
convergence_iter ：比较多少次聚类中心不变之后停止迭代，默认15

c）主要属性
cluster_centers_indices_ : 存放聚类中心的数组
labels_ :存放每个点的分类的数组
n_iter_ : 迭代次数

d) 示例代码

from numpy import unique
from sklearn.cluster import AffinityPropagation
import numpy as np
from sklearn.preprocessing import StandardScaler

# 定义数据集
X = np.random.random((500, 4))
X = StandardScaler().fit_transform(X)
# 定义模型
model = AffinityPropagation(damping=0.5) # 设置damping : 阻尼系数，取值[0.5,1)
# 匹配模型
model.fit(X)
yhat = model.predict(X)  # yhat为集群结果
clusters = len(unique(yhat))  # 类别
1
2
3
4
5
6
7
8
9
10
11
12
13
14

e) 优缺点：
优点：
1>不需要制定最终聚类族的个数
2>已有的数据点作为最终的聚类中心，而不是新生成一个族中心。
3>模型对数据的初始值不敏感。
4>对初始相似度矩阵数据的对称性没有要求。
5>相比与k-centers聚类方法，其结果的平方差误差较小。
缺点：
1>AP算法需要事先计算每对数据对象之间的相似度，如果数据对象太多的话，内存放不下，若存在数据库，频繁访问数据库也需要时间。
2>AP算法的时间复杂度较高，一次迭代大概O(N3)
3>聚类的好坏受到参考度和阻尼系数的影响。

2.聚合聚类（层次聚类）
1）概述
Hierarchical Clustering(层次聚类)：就是按照某种方法进行层次分类，直到满足某种条件为止。
主要分成两类：
a）凝聚：从下到上。首先将每个对象作为一个簇，然后合并这些原子簇为越来越大的簇，直到所有的对象都在一个簇中，或者某个终结条件被满足。
b）分裂：从上到下。首先将所有对象置于同一个簇中，然后逐渐细分为越来越小的簇，直到每个对象自成一簇，或者达到了某个终止条件。（较少用）

2）算法步骤
a）将每个对象归为一类, 共得到N类, 每类仅包含一个对象. 类与类之间的距离就是它们所包含的对象之间的距离.
b）找到最接近的两个类并合并成一类, 于是总的类数少了一个.
c）重新计算新的类与所有旧类之间的距离.
d）重复第2步和第3步, 直到最后合并成一个类为止(此类包含了N个对象).

3）图解过程

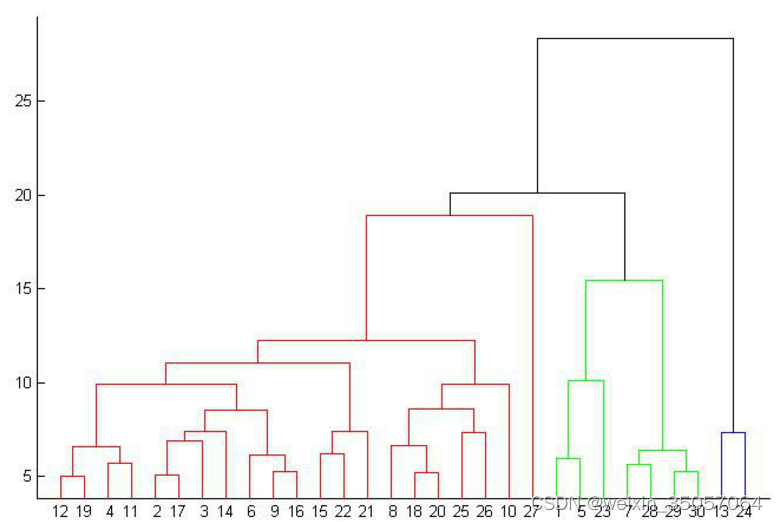
4）Hierarchical Clustering算法函数
a）sklearn.cluster.AgglomerativeClustering
b）主要参数(详细参数)
n_clusters：聚类的个数
linkage：指定层次聚类判断相似度的方法，有以下三种：
ward：组间距离等于两类对象之间的最小距离。（即single-linkage聚类）
average：组间距离等于两组对象之间的平均距离。（average-linkage聚类）
complete：组间距离等于两组对象之间的最大距离。（complete-linkage聚类）
c）主要属性
labels_： 每个数据的分类标签
d) 示例代码：

# 聚合聚类
from numpy import unique
from numpy import where
from sklearn.datasets import make_classification
from sklearn.cluster import AgglomerativeClustering
from matplotlib import pyplot
# 定义数据集
X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4)
# 定义模型
model = AgglomerativeClustering(n_clusters=2)
# 模型拟合与聚类预测
yhat = model.fit_predict(X)
# 检索唯一群集
clusters = unique(yhat)
# 为每个群集的样本创建散点图
for cluster in clusters:
# 获取此群集的示例的行索引
row_ix = where(yhat == cluster)
# 创建这些样本的散布
pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
# 绘制散点图
pyplot.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

3.BIRCH
1）概述
BIRCH的全称是利用层次方法的平衡迭代规约和聚类（Balanced Iterative Reducing and Clustering Using Hierarchies），它是用层次方法来聚类和规约数据。
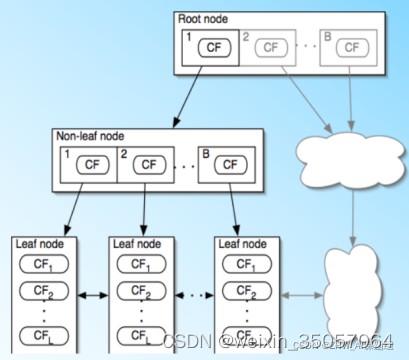
BIRCH算法利用了一个树结构来帮助我们快速的聚类，这个树结构称之为聚类特征树(Clustering Feature Tree，简称CF Tree)。这颗树的每一个节点是由若干个聚类特征(Clustering Feature，简称CF)组成。从右图中我们可以看看聚类特征树的样子：每个节点包括叶子节点都有若干个CF，而内部节点的CF有指向孩子节点的指针，所有的叶子节点用一个双向链表链接起来。
将所有的训练集样本建立了CF Tree，一个基本的BIRCH算法就完成了，对应的输出就是若干个CF节点，每个节点里的样本点就是一个聚类的簇。也就是说BIRCH算法的主要过程，就是建立CF Tree的过程。

2）算法步骤
a) 将所有的样本依次读入，在内存中建立一颗CF Tree
b)（可选）将第一步建立的CF Tree进行筛选，去除一些异常CF节点，这些节点一般里面的样本点很少。对于一些超球体距离非常近的元组进行合并
c)（可选）利用其它的一些聚类算法比如K-Means对所有的CF元组进行聚类，得到一颗比较好的CF Tree。这一步的主要目的是消除由于样本读入顺序导致的不合理的树结构，以及一些由于节点CF个数限制导致的树结构分裂。可以认为是一个半监督K-Means过程。此外，Birch还可以作为其他聚类算法的输入，例如 AgglomerativeClustering。
d)（可选）利用第三步生成的CF Tree的所有CF节点的质心，作为初始质心点，对所有的样本点按距离远近进行聚类。这样进一步减少了由于CF Tree的一些限制导致的聚类不合理的情况。

3）图解过程

4）算法函数
a）sklearn.cluster.Birch
b）主要参数(详细参数)
n_clusters ：聚类的目标个数。（可选）
threshold ：扫描半径（个人理解，官方说法比较绕口），设置小了分类就多。
branches_factor：每个节点中CF子集群的最大数量,默认为50。
c）主要属性
labels_ ：每个数据点的分类
d) 示例代码

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets.samples_generator import make_blobs
from sklearn.cluster import Birch

# X为样本特征，Y为样本簇类别， 共1000个样本，每个样本2个特征，共4个簇，簇中心在[-1,-1], [0,0],[1,1], [2,2]
X, y = make_blobs(n_samples=1000, n_features=2, centers=[[-1,-1], [0,0], [1,1], [2,2]], cluster_std=[0.4, 0.3, 0.4, 0.3], 
                  random_state =9)

##设置birch函数
birch = Birch(n_clusters = None)
##训练数据
y_pred = birch.fit_predict(X)
##绘图
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
plt.show()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

e) 优缺点
优点:
1> 节约内存，所有的样本都在磁盘上，CF Tree仅仅存了CF节点和对应的指针（指向父节点和孩子节点的指针）。
2> 聚类速度快，只需要一遍扫描训练集就可以建立CF Tree，CF Tree的增删改都很快，由于B树是高度平衡的，所以在树上进行插入或查找操作很快，而且合并两个簇只需要两个CF算术相加即可，计算两个簇的距离只需要用到聚类特征。
3> 可识别噪声点，即那些包含数据点少的MinCluster，还可以对数据集进行初步分类的预处理。
缺点:
1> 对非球状的簇聚类效果不好，取决于簇直径和簇间距离的计算方法。
2> 对高维数据聚类效果不好，此时的计算量主要在于SS和簇间距离的计算，此时可以选择Mini Batch K-Means。
3> 结果依赖于数据点的插入顺序。本属于同一个簇的点可能由于插入顺序相差很远而分到不同的簇中。
4> 由于每个节点只能包含一定数目的子节点，最后得出来的簇可能和实际簇相差很大。
Birch适合于处理大数据量和大类别的数据集，但在整个过程中算法一旦中断，一切必须从头再来。
5> 局部性也导致了Birch的聚类效果欠佳。当一个新点要插入B树时，它只跟很少一部分簇进行了相似性（通过计算簇间距离）比较，高的efficient导致低的effective。

4.DBSCAN
1）概述
DBSCAN（Density-Based Spatial Clustering of Applications with Noise,具有噪声的基于密度的聚类方法）是一种基于密度的空间聚类算法。该算法将具有足够密度的区域划分为簇(即要求聚类空间中的一定区域内所包含对象的数目不小于某一给定阈值)，并在具有噪声的空间数据库中发现任意形状的簇，它将簇定义为密度相连的点的最大集合。

2. 算法步骤（大致非详细）
   DBSCAN需要二个参数:扫描半径 (eps)和最小包含点数(min_samples)
   a）遍历所有点，寻找核心点
   b）连通核心点，并且在此过程中扩展某个分类集合中点的个数

3）图解过程

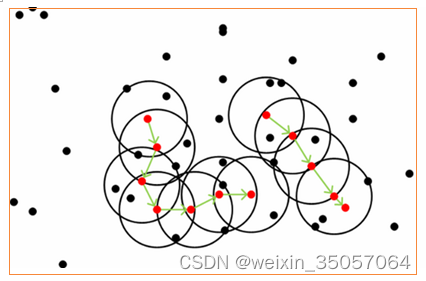
在上图中，第一步就是寻找红色的核心点，第二步就是用绿色箭头联通红色点。图中点以绿色线条为中心被分成了两类。没在黑色圆中的点是噪声点。

4）DBSCAN算法函数
a）sklearn.cluster.DBSCAN
b）主要参数（详细参数）
eps:两个样本之间的最大距离，即扫描半径
min_samples ：作为核心点的话邻域(即以其为圆心，eps为半径的圆，含圆上的点)中的最小样本数(包括点本身)。
c）主要属性
core_sample_indices_:核心样本指数。（此参数在代码中有详细的解释）
labels_:数据集中每个点的集合标签给,噪声点标签为-1。
d) 代码示例：

# dbscan 聚类
from numpy import unique
from numpy import where
from sklearn.datasets import make_classification
from sklearn.cluster import DBSCAN
from matplotlib import pyplot
# 定义数据集
X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4)
# 定义模型
model = DBSCAN(eps=0.30, min_samples=9)
# 模型拟合与聚类预测
yhat = model.fit_predict(X)
# 检索唯一群集
clusters = unique(yhat)
# 为每个群集的样本创建散点图
for cluster in clusters:
# 获取此群集的示例的行索引
row_ix = where(yhat == cluster)
# 创建这些样本的散布
pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
# 绘制散点图
pyplot.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

5.K-均值
1）概述
kmeans算法又名k均值算法,K-means算法中的k表示的是聚类为k个簇，means代表取每一个聚类中数据值的均值作为该簇的中心，或者称为质心，即用每一个的类的质心对该簇进行描述。
其算法思想大致为：先从样本集中随机选取 k个样本作为簇中心，并计算所有样本与这 k个“簇中心”的距离，对于每一个样本，将其划分到与其距离最近的“簇中心”所在的簇中，对于新的簇计算各个簇的新的“簇中心”。
根据以上描述，我们大致可以猜测到实现kmeans算法的主要四点：
   （1）簇个数 k 的选择
   （2）各个样本点到“簇中心”的距离
   （3）根据新划分的簇，更新“簇中心”
   （4）重复上述2、3过程，直至"簇中心"没有移动

2）算法步骤
a) 初始化聚类中心
随机选取k个样本，作为初始的聚类中心
=》如何确定k值？
=》1.尝试不同的k值
=》2.根据业务特点
=》3. 根据SSE或轮廓系数
b) 给聚类中心分配样本
计算每个样本与各个聚类中心的距离，把每个样本分配给距离他最近的聚类中心
欧式距离、曼哈顿距离、余弦相似度
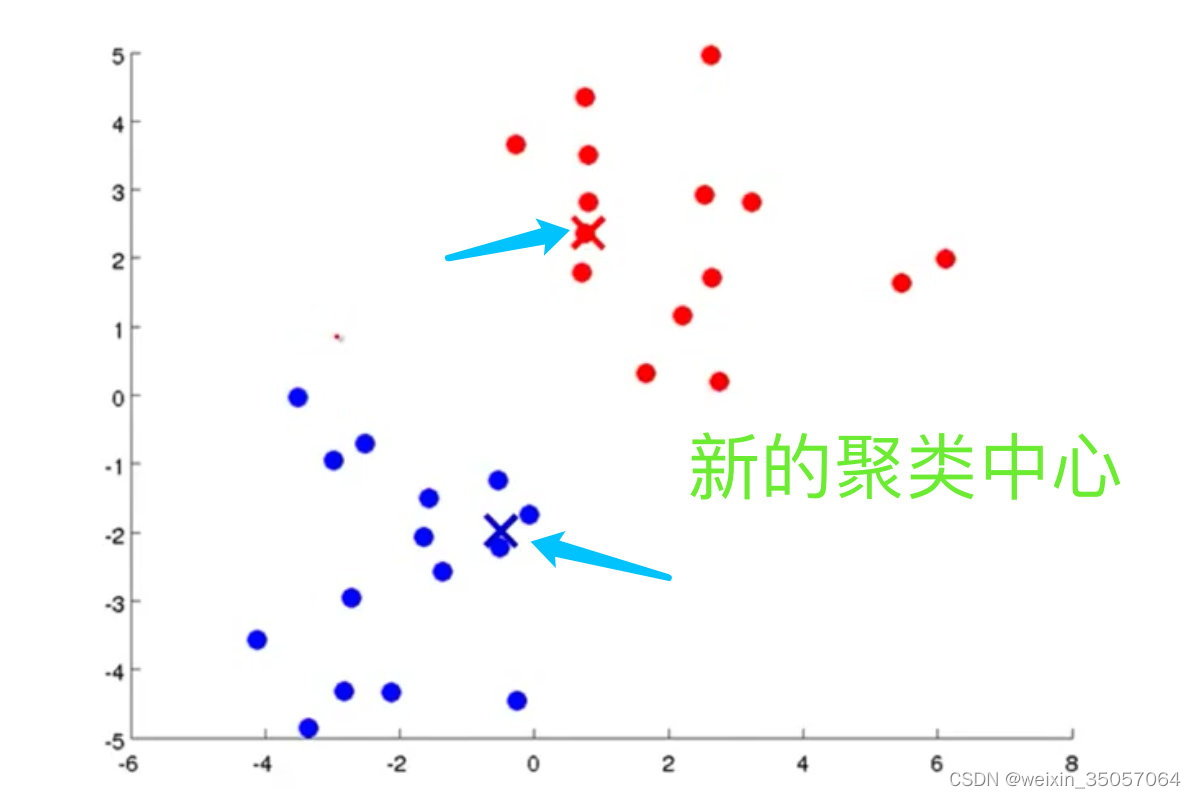
c) 移动聚类中心
新的聚类中心移动到这个聚类所有样本对平均值处
d) 是否停止K-means
质心不再改变，或给定loop最大次数loopLimit

3）图解过程

4）算法函数
a）sklearn.cluster.KMeans
b）主要参数(详细参数)
n_clusters:
k值 缺省值=8 【生成的聚类数，即产生的质心（centroids）数。】
max_iter：
最大迭代次数。 缺省值=300 如果数据集不是凸集，可能很难收敛，此时可以通过指定最大的迭代次数让算法可以及时退出循环。
n_init：
使用不同的初始化质心运行算法的次数。由于K-Means的结果会受初始值影响，属于局部最优的迭代算法，因此需要多跑几次以选择一个较好的聚类效果，默认是10，一般不需要改。k值较大时，可以适当增大这个值。
init：
即初始值选择的方式。可以为完全随机选择’random’,优化过的’k-means++‘或者自己指定初始化的k个质心。一般建议使用默认的’k-means++’。
（１）‘k-means++’ 用一种特殊的方法选定初始质心从而能加速迭代过程的收敛
（２）‘random’ 随机从训练数据中选取初始质心。
（３）如果传递的是一个ndarray，则应该形如 (n_clusters, n_features) 并给出初始质心。

c）主要属性
cluster_centers_：向量，[n_clusters, n_features] (聚类中心的坐标)
Labels_:每个点的分类
inertia_：float形 每个点到其簇的质心的距离之和。
d) 示例代码

# k-means 聚类
from numpy import unique
from numpy import where
from sklearn.datasets import make_classification
from sklearn.cluster import KMeans
from matplotlib import pyplot
# 定义数据集
X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4)
# 定义模型
model = KMeans(n_clusters=2)
# 模型拟合
model.fit(X)
# 为每个示例分配一个集群
yhat = model.predict(X)
# 检索唯一群集
clusters = unique(yhat)
# 为每个群集的样本创建散点图
for cluster in clusters:
# 获取此群集的示例的行索引
row_ix = where(yhat == cluster)
# 创建这些样本的散布
pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
# 绘制散点图
pyplot.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

e) 优缺点
K-Means的主要优点：
1）原理简单，容易实现
2）可解释度较强
K-Means的主要缺点：
1）K值很难确定
2）局部最优
3）对噪音和异常点敏感
4）需样本存在均值（限定数据种类）
5）聚类效果依赖于聚类中心的初始化
6）对于非凸数据集或类别规模差异太大的数据效果不好

6.Mini-Batch K-均值
1）概述
Mini Batch K-Means算法是K-Means算法的一种优化方案，采用小批量的数据子集减小计算时间，同时仍试图优化目标函数，这里所谓的小批量是指每次训练算法时所随机抽取的数据子集，采用这些随机产生的子集进行训练算法，大大减小了计算时间，与其他算法相比，减少了k-均值的收敛时间，小批量k-均值产生的结果，一般只略差于标准算法。

Mini Batch KMeans使用了一个种叫做Mini Batch（分批处理）的方法对数据点之间的距离进行计算。Mini Batch的好处是计算过程中不必使用所有的数据样本，而是从不同类别的样本中抽取一部分样本来代表各自类型进行计算。由于计算样本量少，所以会相应的减少运行时间，但另一方面抽样也必然会带来准确度的下降。

2）算法步骤
迭代步骤：
1：从数据集中随机抽取一些数据形成小批量，把他们分配给最近的质心
2：更新质心
与K均值算法相比，数据的更新是在每一个小的样本集上。对于每一个小批量，通过计算平均值得到更新质心，并把小批量里的数据分配给该质心，随着迭代次数的增加，这些质心的变化是逐渐减小的，直到质心稳定或者达到指定的迭代次数，停止计算

3）图解过程

4）算法函数
a）sklearn.cluster.MiniBatchKMeans
b）主要参数(详细参数)

c）主要属性

d) 示例代码

# mini-batch k均值聚类
from numpy import unique
from numpy import where
from sklearn.datasets import make_classification
from sklearn.cluster import MiniBatchKMeans
from matplotlib import pyplot
# 定义数据集
X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4)
# 定义模型
model = MiniBatchKMeans(n_clusters=2)
# 模型拟合
model.fit(X)
# 为每个示例分配一个集群
yhat = model.predict(X)
# 检索唯一群集
clusters = unique(yhat)
# 为每个群集的样本创建散点图
for cluster in clusters:
# 获取此群集的示例的行索引
row_ix = where(yhat == cluster)
# 创建这些样本的散布
pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
# 绘制散点图
pyplot.show()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

7.Mean Shift
1. 概述
Mean-shift（即：均值迁移）的基本思想：在数据集中选定一个点，然后以这个点为圆心，r为半径，画一个圆(二维下是圆)，求出这个点到所有点的向量的平均值，而圆心与向量均值的和为新的圆心，然后迭代此过程，直到满足一点的条件结束。(Fukunage在1975年提出)
后来Yizong Cheng 在此基础上加入了 核函数 和 权重系数 ，使得Mean-shift 算法开始流行起来。目前它在聚类、图像平滑、分割、跟踪等方面有着广泛的应用。
2. 图解过程
为了方便大家理解，借用下几张图来说明Mean-shift的基本过程。

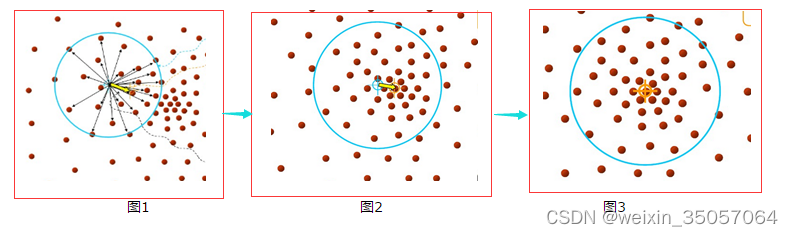
由上图可以很容易看到，Mean-shift 算法的核心思想就是不断的寻找新的圆心坐标，直到密度最大的区域。
3. Mean-shift 算法函数
a）核心函数：sklearn.cluster.MeanShift(核函数：RBF核函数)
由上图可知，圆心(或种子)的确定和半径(或带宽)的选择，是影响算法效率的两个主要因素。所以在sklearn.cluster.MeanShift中重点说明了这两个参数的设定问题。
b）主要参数
bandwidth ：半径(或带宽)，float型。如果没有给出，则使用sklearn.cluster.estimate_bandwidth计算出半径(带宽).（可选）
seeds :圆心（或种子），数组类型，即初始化的圆心。（可选）
bin_seeding ：布尔值。如果为真，初始内核位置不是所有点的位置，而是点的离散版本的位置，其中点被分类到其粗糙度对应于带宽的网格上。将此选项设置为True将加速算法，因为较少的种子将被初始化。默认值：False.如果种子参数(seeds)不为None则忽略。
c）主要属性
cluster_centers_ : 数组类型。计算出的聚类中心的坐标。
labels_ :数组类型。每个数据点的分类标签。
d) 示例代码

# 均值漂移聚类
from numpy import unique
from numpy import where
from sklearn.datasets import make_classification
from sklearn.cluster import MeanShift
from matplotlib import pyplot
# 定义数据集
X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4)
# 定义模型
model = MeanShift()
# 模型拟合与聚类预测
yhat = model.fit_predict(X)
# 检索唯一群集
clusters = unique(yhat)
# 为每个群集的样本创建散点图
for cluster in clusters:
# 获取此群集的示例的行索引
row_ix = where(yhat == cluster)
# 创建这些样本的散布
pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
# 绘制散点图
pyplot.show()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

8.OPTICS

9.光谱聚类
1）概述
Spectral Clustering(SC,即谱聚类)，是一种基于图论的聚类方法,它能够识别任意形状的样本空间且收敛于全局最有解，其基本思想是利用样本数据的相似矩阵进行特征分解后得到的特征向量进行聚类.它与样本特征无关而只与样本个数有关。

基本思路：将样本看作顶点,样本间的相似度看作带权的边,从而将聚类问题转为图分割问题:找到一种图分割的方法使得连接不同组的边的权重尽可能低(这意味着组间相似度要尽可能低),组内的边的权重尽可能高(这意味着组内相似度要尽可能高).

2）图解过程

如上图所示，断开虚线，六个数据被聚成两类。
3）Spectral Clustering算法函数
a）核心函数：sklearn.cluster.SpectralClustering
因为是基于图论的算法，所以输入必须是对称矩阵。
b）主要参数(参数较多，详细参数)
n_clusters：聚类的个数。（官方的解释：投影子空间的维度）
affinity：核函数，默认是’rbf’，可选：“nearest_neighbors”，“precomputed”,"rbf"或sklearn.metrics.pairwise_kernels支持的其中一个内核之一。
gamma :affinity指定的核函数的内核系数，默认1.0

c）主要属性

labels_ ：每个数据的分类标签
d) 示例代码

# spectral clustering
from numpy import unique
from numpy import where
from sklearn.datasets import make_classification
from sklearn.cluster import SpectralClustering
from matplotlib import pyplot
# 定义数据集
X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4)
# 定义模型
model = SpectralClustering(n_clusters=2)
# 模型拟合与聚类预测
yhat = model.fit_predict(X)
# 检索唯一群集
clusters = unique(yhat)
# 为每个群集的样本创建散点图
for cluster in clusters:
# 获取此群集的示例的行索引
row_ix = where(yhat == cluster)
# 创建这些样本的散布
pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
# 绘制散点图
pyplot.show()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

10.高斯混合
1）概述 高斯混合聚类
核心思想：
它是一种基于概率分布的聚类算法，它是首先假设每个簇符合不同的高斯分布，也就是多元正态分布，说白了就是每个簇内的数据会符合一定的数据分布。

假设数据集是按照一定统计过程产生的，那么聚类的过程就是通过样本学习相应统计分布模型的参数

它的大致流程就是首先假设k个高斯分布，然后判断每个样本符合各个分布的概率，将该样本划为概率最大的那个分布簇内，然后一轮后，进行更新我们的高斯分布参数，就会用到我们的极大似然估计，然后再基于新的分布去计算符合各个分布的概率，不断迭代更新，直至模型收敛达到局部最优解，常见的算法就是EM算法，它会同时估计出每个样本所属的簇类别以及每个簇的概率分布的参数。

概率密度常记为：
意思就是在参数为一定值的情况下符合的分布，对应相应的概率密度函数。

2）算法步骤
Input: 簇的个数K, 阈值epsilon, 最大迭代次数
Output: 混合模型参数（包括所有分模型构成的均值向量，alpha向量，方差向量）
Step1: 采用Kmeans方法初始化混合模型参数
Step2: EM算法学习参数
Step3: 根据学习得到的参数，计算每个样本对各个分模型的相应度（即样本来子分模型的概率），样本归属于相应度最大的分模型对应的簇

3）图解过程

4）算法函数
a）sklearn.mixture.GaussianMixture
b）主要参数(详细参数)
n_components ：混合元素（聚类）的数量，默认为1
covariance_type：描述要使用的协方差参数类型的字符串，必选一个(‘full’ , ‘tied’, ‘diag’, ‘spherical’)，默认为full。
tol：float类型, 默认值： 0.001.收敛阈值，当平均增益低于这个值时迭代停止。
reg_covar：float类型, 协方差对角线上的非负正则化参数，默认值： 1e-6 接近于0.
max_iter：最大迭代次数，默认为100
n_init：执行初始化操作数量，保持最好的结果，默认为1

c）主要属性
weights_ : array-like, shape (n_components,)，每个混合元素权重
means_ : array-like, shape (n_components, n_features)，每个混合元素均值
covariances_ : array-like，每个混合元素的协方差，它的形状依靠协方差类型

d) 示例代码

# 高斯混合模型
from numpy import unique
from numpy import where
from sklearn.datasets import make_classification
from sklearn.mixture import GaussianMixture
from matplotlib import pyplot
# 定义数据集
X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4)
# 定义模型
model = GaussianMixture(n_components=2)
# 模型拟合
model.fit(X)
# 为每个示例分配一个集群
yhat = model.predict(X)
# 检索唯一群集
clusters = unique(yhat)
# 为每个群集的样本创建散点图
for cluster in clusters:
# 获取此群集的示例的行索引
row_ix = where(yhat == cluster)
# 创建这些样本的散布
pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
# 绘制散点图
pyplot.show()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25