连续/离散的控制系统阶跃测试（包括MATLAB里的step()函数）

阶跃测试

只要是连续时间系统，无论是传递函数还是连续状态空间形式的模型，直接可以用**step()**做阶跃测试；但是对于离散系统而言，不能用step()函数，可以自行编写代码，如下。

1、离散系统：x(k+1)=Ax(k)+Bu(k)

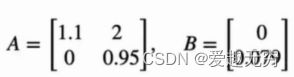
离散系统阶跃响应不能用step()函数，可以自行编写

close all;
clear all;
A=[1.1 2;0 0.95];B=[0;0.079];

total = 100;
x = zeros(2,total+1);
u = zeros(1,total);
u(1) = 1;
t = zeros(1,total);

for i=1:total
    
    t(i) = i-1;
    x(:,i+1) = A*x(:,i) + B*u(:,i);
end

figure(1);
subplot(3,1,1);
plot(t,x(1,1:total));
ylabel('x1')
hold on;
grid on;

subplot(3,1,2);
plot(t,x(2,1:total));
ylabel('x2')
hold on;
grid on;

subplot(3,1,3);
plot(t,u(1:total));
ylabel('u')
hold on;
grid on;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

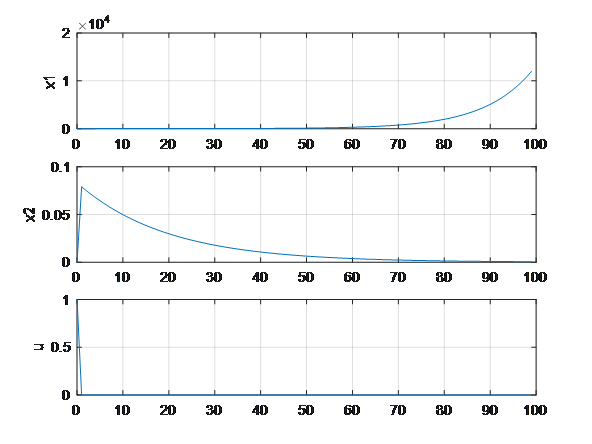
可见系统自身不稳定，因为离散系统的特征值有在单位圆外，如下

2、连续系统：x’=Ax+Bu或y=G(s)u

一个是连续状态空间模型，一个是传递函数模型

2.1 传递函数形式：

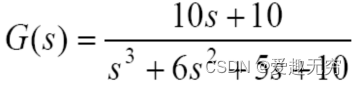
MATLAB里写成传函形式，并做阶跃测试**step()**函数

2.2 化成连续状态空间形式

再做阶跃

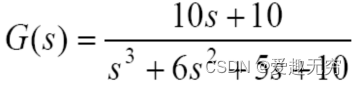
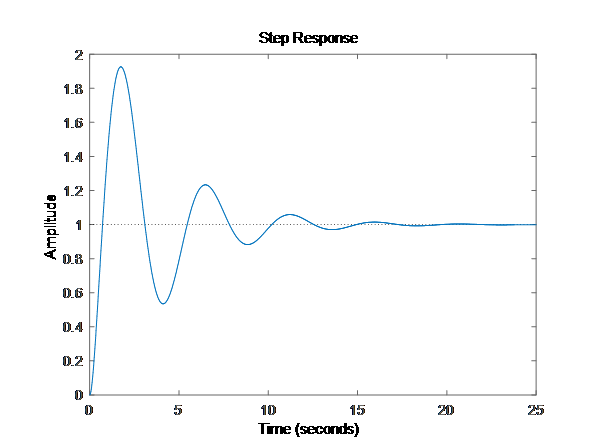
不管是传函，还是连续状态空间，step()测试结果相同，说明系统稳定，因为状态矩阵特征值都<0；

eig(A)

ans =

-5.4178 + 0.0000i
-0.2911 + 1.3270i
-0.2911 - 1.3270i

2.3 连续状态空间形式化成离散状态空间形式

（1）对传递函数进行离散

得到的是离散时间传递函数，z变换
（2）对连续状态空间模型进行离散

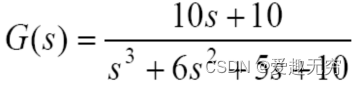
得到的是离散状态空间模型
（3）对离散状态空间模型做阶跃测试
离散系统阶跃响应不能用step()函数，可以自行编写，就是本文第1节，下面继续写一遍：

A = [0.5307 -0.2069 -0.1864;0.1491 0.978 -0.02058;0.01647 0.1985  0.9986];B = [0.1491;0.01647;0.001152];C = [0 2.5 1.25];%得到的离散状态空间模型

total = 100;
x = zeros(3,total+1);
u = zeros(1,total);
u(1) = 1;
y = zeros(1,total);
t = zeros(1,total);

for i=1:total
    
    t(i) = i-1;
    x(:,i+1) = A*x(:,i) + B*u(:,i);
    y(:,i+1) = C*x(:,i+1);
end

figure(1);
subplot(3,1,1);
plot(t,x(1,1:total));
ylabel('x1')
hold on;
grid on;

subplot(3,1,2);
plot(t,x(2,1:total));
ylabel('x2')
hold on;
grid on;

subplot(3,1,3);
plot(t,x(3,1:total));
ylabel('x3')
hold on;
grid on;

figure(2)
subplot(2,1,1);
plot(t,u(1:total));
ylabel('u')
hold on;
grid on;

subplot(2,1,2);
plot(t,y(1:total));
ylabel('y')
hold on;
grid on;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

图形如下：


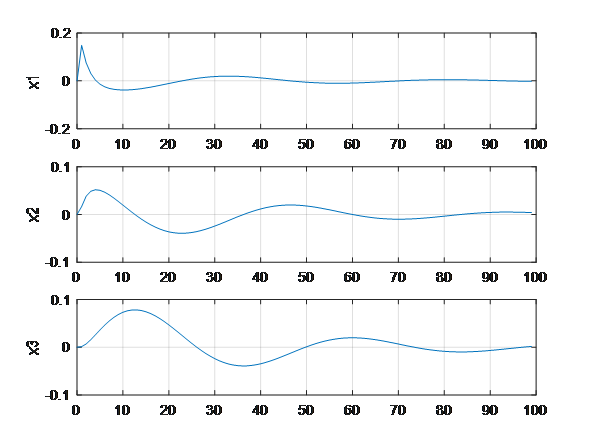
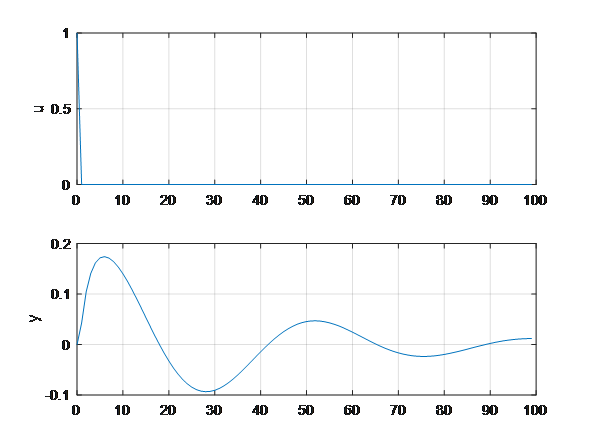
化成离散系统后，仍然稳定。