形式化验证笔记

参考视频：

• 形式化验证的原理与新应用
• 【DatenLord达坦科技】形式化验证入门(我强推！！！！！)

形式化验证：在状态机表征的空间里面进行搜索，验证某个模型是否按规范执行且测试覆盖率达到100%
方法：将规范(可选)和代码变为数学公式，再将公式放入定理证明器

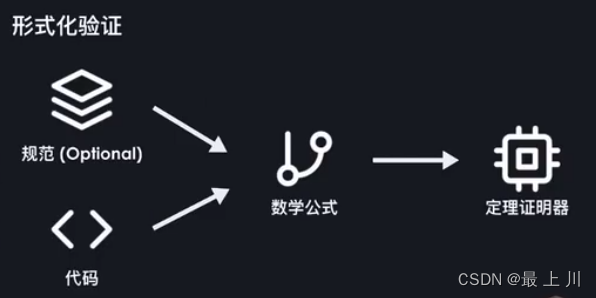
例子

第一种作用：生成测试用例

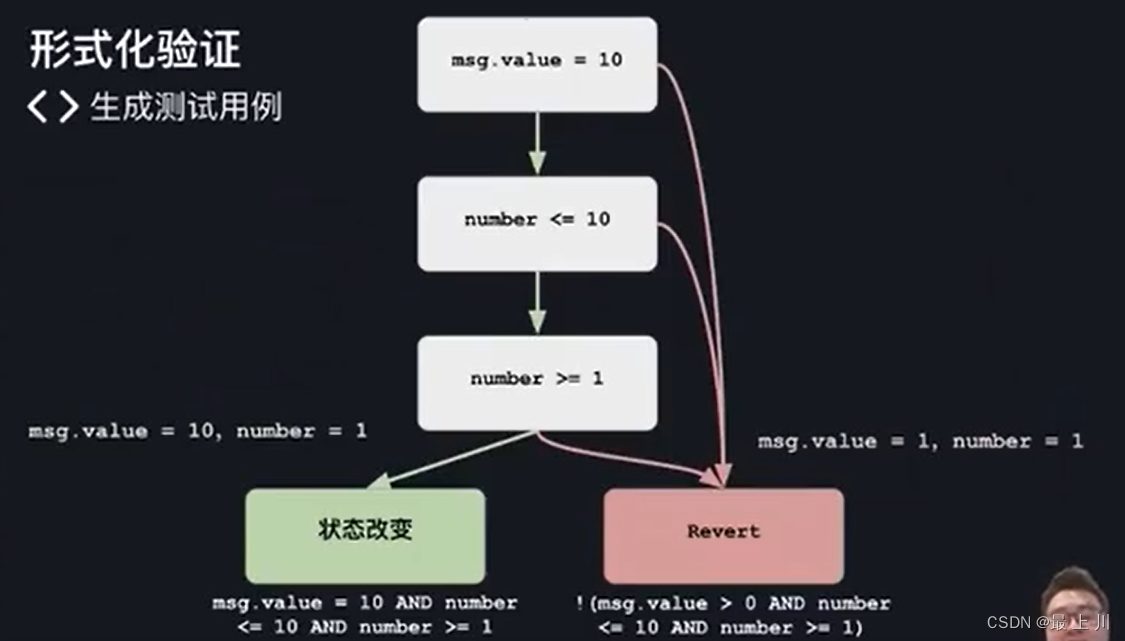
第二种作用：验证程序是否符合规范
第一步：把控制流程图转成表达式

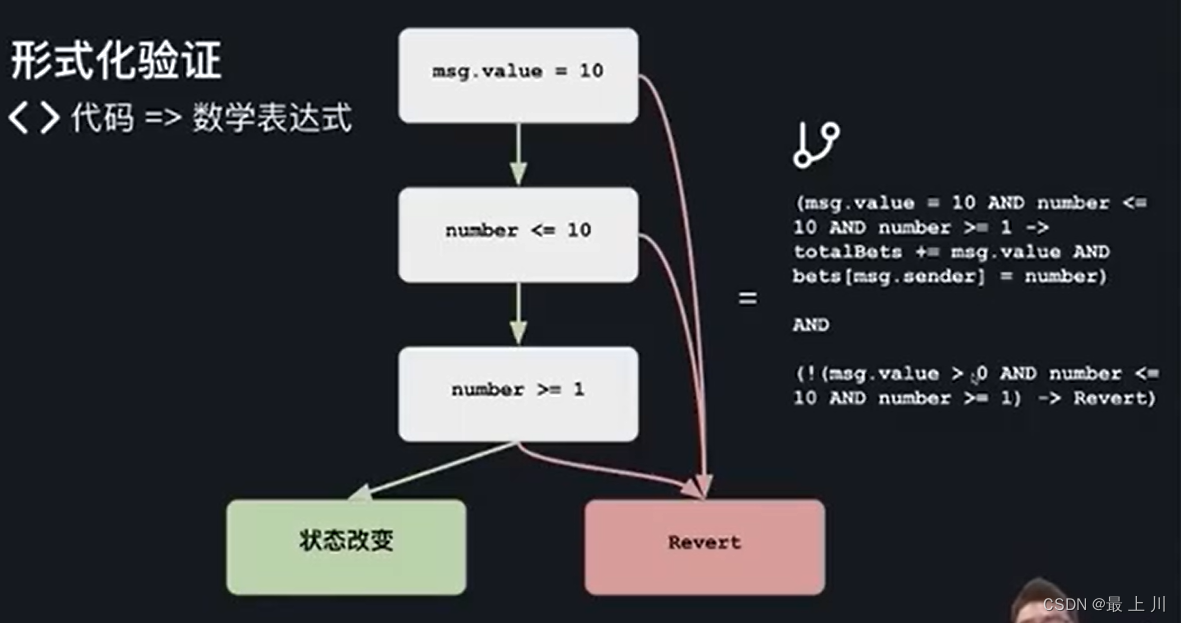
第二步：将规范加入表达式
但是该做法会导致只能找到正确值而不是违反规范的路径，所以要将规范取非，以匹配违反规范的情况

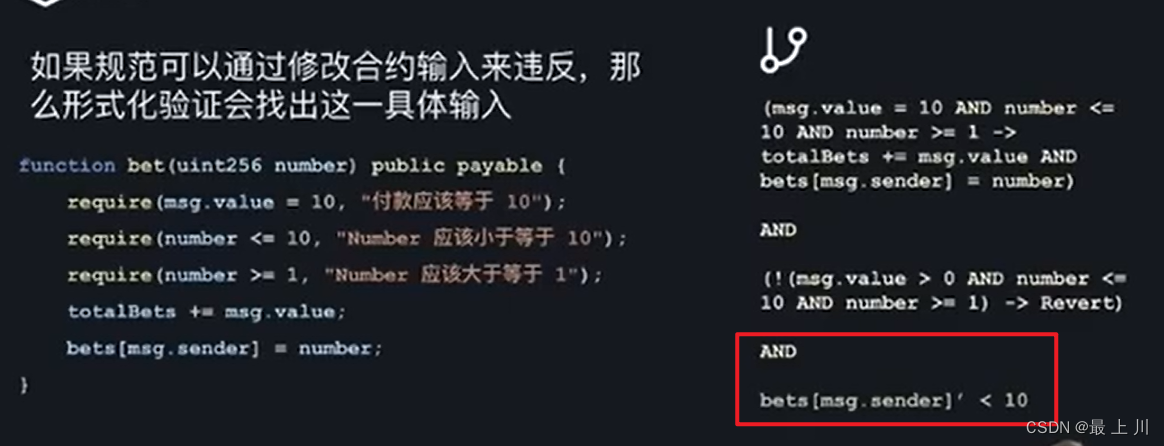
进一步，因为一般程序很复杂，所以是用验证器，让计算机进行计算

上述只能进行当前场景一次的验证，于是为了考虑时间属性，引入了LTL
比如要限制一个计数器永远小于10，下面的程序确实可以限制单次不会增加超过10，但是多次之后cnt就会超过10
所以我们就要引入G、U、F、X这种时态

int cnt = 0;
void add(num){
	if(num>=10)报错;
	else cnt+=num;
}
1
2
3
4
5

模糊测试TODO

结合LLM

通过LLM，使用自然语言生成规范

LTL

LTL主要研究的是trace，每个状态其实就是第一个label的变换

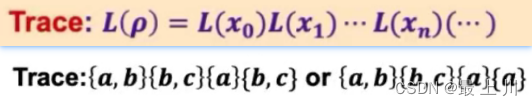
注意$ab{c}^{\ast }$的星号表示未知的有限次数，$ab{c}^{\omega }$的w表示未知的无限次数

LTS的乘积

label transition system
就是两个状态机的乘积
即两边的状态做笛卡尔积
转换关系、原子命题、标签函数取并集

将待检测代码和要检查的属性(注意规范就是定义要满足的属性)，两个状态机乘起来
比如把车行灯和人行灯进行乘起来

可以看到2*3=6
在这个状态机里找有没有期待的非法状态出现
然后因为出现了{g,w}，即车绿灯时，人穿过马路

LTP

线性时间属性
形式化方法与数理逻辑不一样的点
即形式化方法引入了时间(离散的)概念
形式化方法因为有无限时间，所以会展开成很大的路径空间

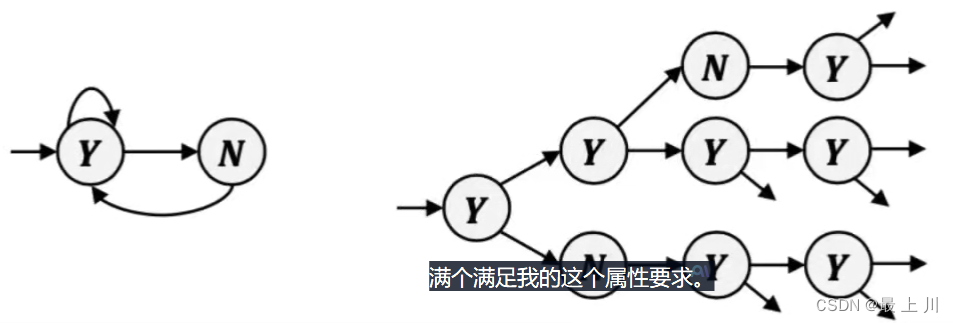
我们要做的就是找到一条路径，满足我们定义的属性要求(一般就是找非法路径，没有说明程序合理)

安全性&不变性(safety & invariant)

永远不会发生坏的事情
某些属性应适用于所有可访问状态

所以就是在有限字上找一个坏前缀(有限步骤上会不会有坏状态，如果当前已经坏了，那么后面肯定就不能走了)

活性(liveness)

好事最终会发生(test case不能做到，因为测试时长是有限的)
所以是形式化验证强大的地方

通过一个有环的有限状态自动机表示一个无限序列
所以就是检查环上是否最终会出现这个好事

有几种，比如最终发生一次，会发生多次最终发生一次，每次等待了就一定能发生

LTL

注意LTL定义上只有U和F，但是衍生出了
G的意思是每一跳都要满足
F的意思是最终某一跳会满足
还有O表示下一跳
F($\varphi$) := True U $\varphi$
G($\varphi$) := !(F(!$\varphi$))

应用：

• 安全性：线程P1和P2不会同时进入临界区：$G(!(cri{t}_1\&cri{t}_2))$
• 活性：两个线程最终都能进入临界区，不会饥饿：$(G(F(cri{t}_1))\&G(F(cri{t}_2)))$
• 强活性：只要等待了就最终能进去：
  

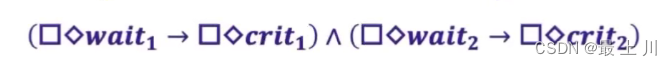
例子：下图表示

• 外面包着G，表示每一跳都保持这个属性
• 先红灯，然后红灯亮一会，最终变黄灯
• 黄灯也亮一会，最终变绿灯
  

CTL

computing tree logic
计算树逻辑比LTL多了全称和存在量词，是对全局来看的
LTL就是不能表达存在某条路径，他默认带的是全称量词

将需求规范形式化

工程实践

TLA+

两种代码编写方式：TLA+和PlusCal
用状态机描述代码，有穷尽的状态

demo

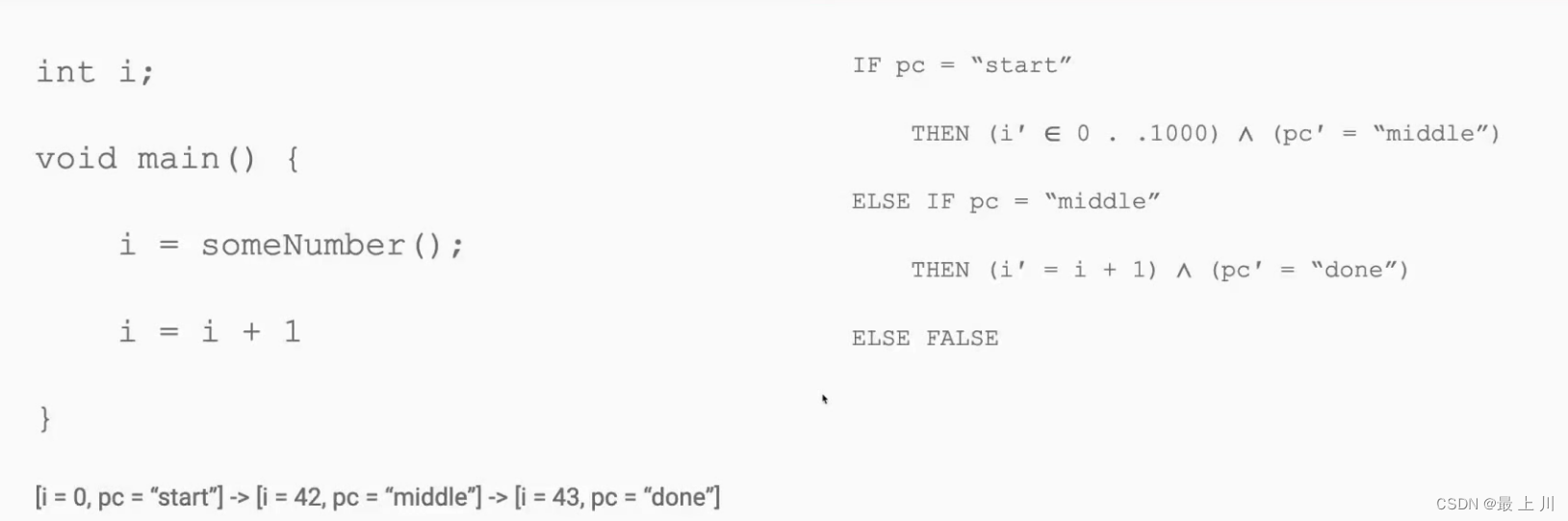
进一步改进

把or再改下

TLA真实代码