MMoE: 基于多门专家混合的多任务学习任务关系建模

文章链接：Modeling Task Relationships in Multi-task Learning with Multi-gate Mixture-of-Experts

发表会议: KKD 2018 （Knowledge Discovery and Data Mining，数据挖掘领域顶会）

1.背景介绍

目前应用的MoE模型结构普遍采用单门控设计，在单门控(Single-Gate) 网络的基础上可以分为单栅(Single-Gated) 网络和多栅(Multi-Gated) 网络。这两类门控网络的主要区别在于每次选择专家的数量，前者每次只选择概率分布最大的一个专家，后者则选择概率分布上Top-K个专家。
那么有没有一种MoE架构采用的不是单门控网络，而是采用多门控(Multi-Gate) 网络呢?
Google scholar查找发现，在2018年KDD伦敦会议上，有学者提出了基于多门专家混合的多任务学习任务关系建模，也就是本次学习的文章。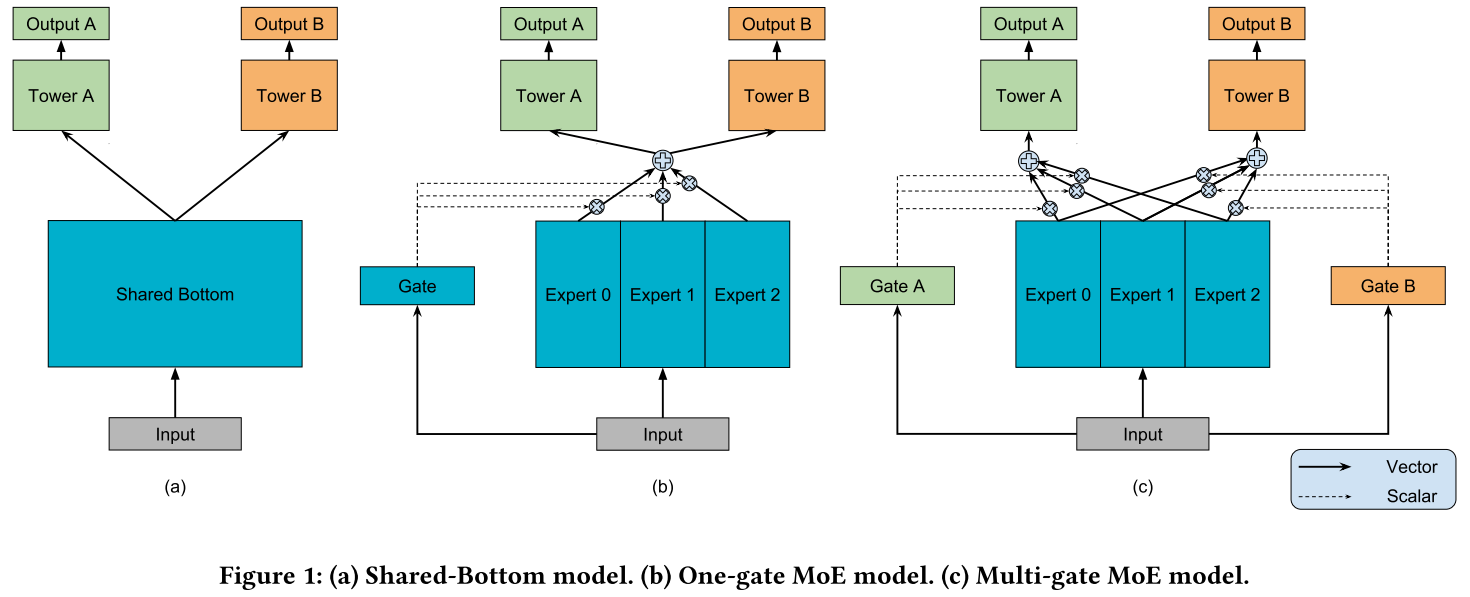

---

Recommendation System

推荐系统(Recommendation System,RS)是一类利用算法和数据分析技术来预测用户对物品（如商品、服务、信息等）喜好程度的系统。其主要目的是帮助用户在海量信息中快速找到符合其个性化需求的内容，提升用户体验和用户满意度。

推荐算法：推荐系统采用各种不同的算法来生成推荐结果。主要的算法包括：

- 协同过滤：基于用户行为历史和用户群体行为的相似性来进行推荐。

- 内容过滤：基于物品的属性和用户的兴趣进行匹配，通常需要提前对物品进行特征提取。

- 矩阵分解：通过将用户-物品交互矩阵分解为两个低秩矩阵，来学习用户和物品的表示。

- 深度学习方法：通过深度学习模型来学习用户和物品的表示。
1
2
3
4
5
6
7

采用深度神经网络模型的推荐系统通常需要同时优化多个目标。例如，在向用户推荐电影时，我们不但希望用户不仅购买并观看电影，还希望他们在看完电影后做出评价或反馈。也就是说，我们想要创建一个模型来同时预测用户的购买行为和他们的评分，即多任务学习。

---

Multi-task Learning

多任务学习（Multi-Task Learning, MTL）是一种机器学习方法，其主要目标是通过同时学习多个相关任务来提高模型的性能。相比于单一任务学习，MTL 在训练过程中利用了任务之间的共享知识和信息，从而可以更好地泛化到新的任务或数据。

多任务学习模型的一般流程和关键要素：

事实上，许多基于DNN的多任务学习模型对数据分布差异、任务间关系等因素都很敏感。来自任务差异的内在冲突实际上可能会损害至少部分任务的预测，即优化冲突（optimization conflict），特别是当所有任务广泛共享模型参数时。

为了提高任务间的差异化程度，一个简单的方式是为每个任务添加更多的参数模型。特定于任务的参数与共享的参数，两者相互配合，可以在训练时取得更好的性能，但这些额外参数会带来额外的计算成本。

---

Synthetic Data Generation

合成数据生成（Synthetic Data Generation，SDG）是一种通过模拟或生成数据来扩充现有数据集的方法。这些生成的数据在统计上与真实数据集相似，但是并非来自实际观测或采集，而是通过模型或规则生成的。

通过使用合成数据，我们可以很容易地测量和控制任务相关性。

---

MMoE

多门专家混合(Multi-gate Mix-of-Experts, MMoE)模型，由多个专家和多个门控网络组成。MMoE显式地对任务关系建模，并学习特定于任务的功能，以利用共享表示。它允许自动分配参数来捕获共享的任务信息或特定于任务的信息，从而避免了为每个任务添加许多新参数的需要。

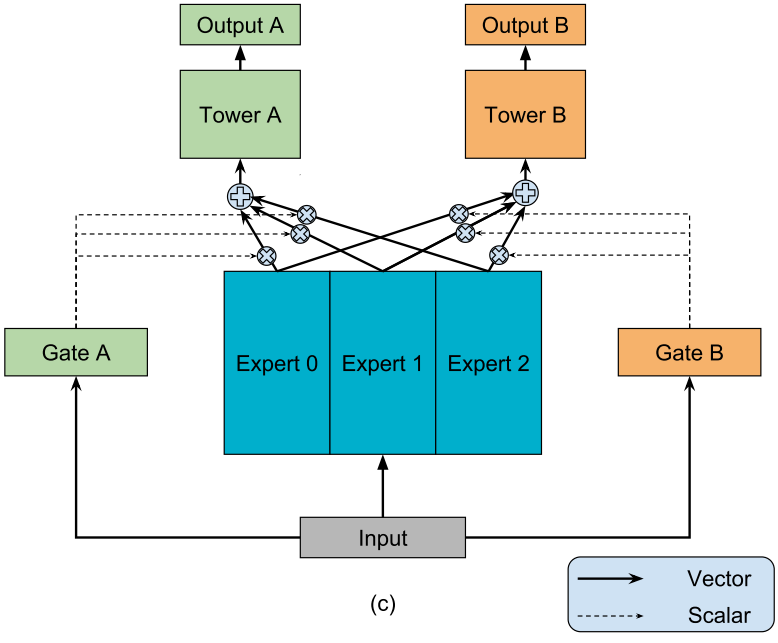
MMoE的主干是建立在最常用的共享底部多任务DNN结构上的。共享底层模型结构如图（a）所示，其中输入层之后的几个底层在所有任务之间共享，然后每个任务在底层表示的顶部都有一个单独的网络“塔”。

MMoE模型，图（c）所示，有一组底层网络，但不是所有任务共享一个底层网络，底层网络被划分为多个专家，每个专家是一个前馈网络。

每个任务引入一个门控网络。门控网络采用输入特征和输出softmax门，将具有不同权重的专家组装在一起，允许不同的任务以不同的方式利用专家。然后将组装的专家的结果传递到特定于任务的塔网络中。通过这种方式，针对不同任务的门控网络可以学习专家集合的不同混合模式，从而捕获任务关系。

---

2.内容摘要

文章提出了一种新的多任务学习方法，多门专家混合(MMoE)，它显式地学习从数据中建立任务关系的模型。文章将MMoE结构应用于多任务学习，在所有任务之间共享专家子模型，同时训练一个门控网络来优化每个任务。
为了在具有不同任务相关性级别的数据上验证MMoE的有效性，文章首先将其应用于一个合成数据集，在该数据集上我们控制任务相关性。当任务相关性较低时，所提出的方法比基线方法表现得更好。 根据训练数据和模型初始化的不同程度的随机性，MMoE结构还带来了额外的可训练性优势。

关键技术

MMoE Modeling

给定 $K$ (上图$K=2$)个任务，模型由一个共享底层网络(表示为函数 $f$，设 $i$ 为专家编号，$k$ 为其中一个任务，则共享层输出可表示为 $$f^k(x)=\sum _{i=1}^n{g}^k(x{)}_i\cdot f_i(x)$$ 其中门控网络 $g^k$ 是一个通过softmax激活的简单线性变换，$$g^k(x)=softmax(W_{gk}x)$$ $W_{gk}\in {\mathbb{R}}^{n\times d}$ 是一个可训练的矩阵。$n$ 为专家数量，$d$ 为特征维数。
在通过门控网络和共享层计算后，对应的任务 $k$ 会进入到网络“塔” $h^k$ 进行最后计算。对于任务 k，模型输出可以表示为:
$$y_k=h^k(f^k(x))$$

每个门控网络 $g^k$ 可以学习“选择”一个专家子集。在MTL的情境下充当参数共享的概率分布。举个例子，如果每个门控网络只选择一个得分最高的专家，那么每个门网络实际上将输入空间线性划分为n个区域，每个区域对应一个专家。

MMoE能够以一种复杂的方式对任务关系进行建模，来确定不同的门所导致的分离如何相互重叠。如果任务的相关性较低，那么共享专家将受到惩罚，这些任务的控制网络将学会使用不同的专家。

与共享底层模型相比，MMoE只有几个附加的门控网络，门控网络中模型参数的数量可以忽略不计。因此，整个模型仍然尽可能地享受多任务学习中知识转移的好处。

---

Synthetic Dataset

多任务学习模型的性能在很大程度上依赖于数据中固有的任务关联性。在实际应用中，很难直接研究任务关联性如何影响多任务模型，因为我们无法轻易地改变任务间的关联性并观察其效果。

为了建立对这一关系的实证研究，本文使用合成数据，可以很容易地测量和控制任务相关性。本文生成了两个回归任务，并使用这两个任务标签的皮尔逊相关性作为任务关系的定量指标。

合成数据步骤如下：

1. 给定输入特征维数 $d$，生成两个正交的单位向量 $u_1,u_2\in {\mathbb{R}}^d$
   $$u_1^T{u}_2=0,||u_1|{|}_2=1,||u_2|{|}_2=1$$
2. 给定一个比例常数 $c$ 和一个皮尔逊相关值 $-1\le p\le 1$ 生成两个权重向量$w_1$ $w_2$:
   $$w_1=c\cdot u_1,w_2=c\cdot (p{u}_1+\sqrt{(1-p^2)u_2})$$
3. 对输入数据点 $x\in R\dots \dots d$ 的每个元素从 $N(0,1)$ 中随机抽样
4. 为两个回归任务生成两个标签 $y1,y2$:
   $$y_1=w_1^{T}x+\sum _{i=1}^{m}sin(\alpha w_1^{T}x+{\beta }_i)+{ϵ}_1$$ $$y_2=w_2^{T}x+\sum _{i=1}^{m}sin(\alpha w_2^{T}x+{\beta }_i)+{ϵ}_2$$其中 ${\alpha }_i,{\beta }_i,i=1,2,...,m$ 是控制正弦函数形状的给定参数，并且
   $${ϵ}_1,{ϵ}_2\stackrel{i.i.d}{\sim }\mathcal{N}(0,0.01)$$
5. 重复(3)和(4)，直到生成足够的数据

---

实验结果

Census-income Data

本次测试数据集为”人口普查收入“数据集，UCI人口普查收入数据集是从1994年人口普查数据库中提取的。它包含了299285个美国成年人的人口统计信息实例。

本文构建了两个多任务学习问题，将其中的一些特征设置为预测目标，并计算了超过10,000个随机样本的任务标签的Pearson相关性绝对值:

1. Group1:
   任务 1: 预测收入是否超过50K$;
   任务 2: 预测这个人的婚姻状况是否从未结婚。
   P = 0.1768
2. Group2:
   任务 1: 预测教育水平是否至少为大学;
   任务 2: 预测这个人的婚姻状况是否从未结婚。
   P = 0.2373

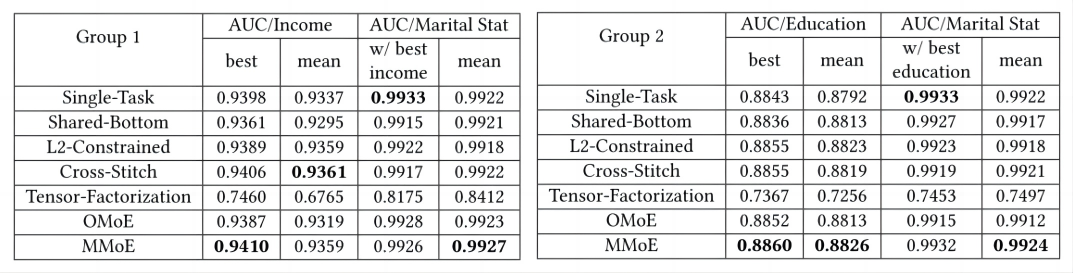
表1和表2显示了两组的结果,报告了运行400次以上的平均AUC。

考虑到任务关联性(粗略地用皮尔逊相关性来衡量)在两组中都不是很强，共享底层模型几乎总是多任务模型中最差的。

L2 - restricted和Cross-Stitch都为每个任务提供了单独的模型参数，并为如何学习这些参数添加了约束，因此比Shared-Bottom执行得更好。

然而，模型参数学习的约束很大程度上依赖于任务关系假设，与MMoE使用的参数调制机制相比，任务关系假设的灵活性较差。

---

大规模内容推荐

在谷歌Inc.的一个大型内容推荐系统上进行实验，该系统中的推荐来自于为数十亿用户生成的数亿个独立条目。具体来说，给定用户当前消费商品的行为，该推荐系统的目标是向用户显示下一个要消费的相关商品的列表。

设置的DNN被训练为优化两种类型的排名目标:

1. 优化与参与度相关的目标，如点击率和参与度时间;
2. 优化满意度相关目标，如满意率等。

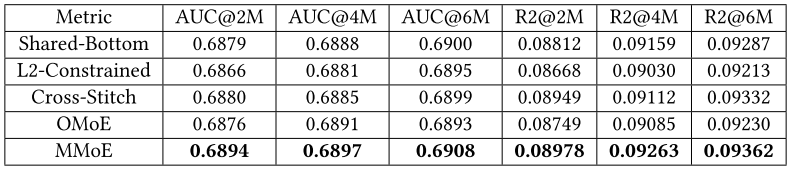
上表显示了训练200万步(100亿个示例，批量大小为1024)、400万步和600万步之后的结果。MMoE在这两个指标上都优于其他模型。L2-Constrained 和 Cross-Stitch比 Shared-Bottom 更糟糕。这可能是因为这两个模型是建立在两个单独的单任务模型之上的，并且有太多的模型参数需要很好的约束。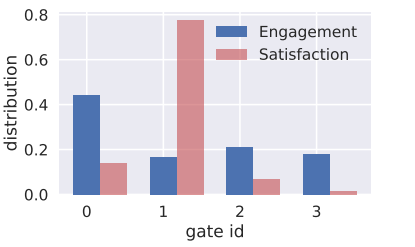

上图显示了每个任务的softmax门的分布。MMoE学习了这两个任务之间的差异，并自动平衡了共享和非共享参数。

由于满意度子任务的标签比参与度子任务的标签更稀疏，因此满意度子任务的门更集中于单个专家。

---

3.文章总结

本文提出了一种新的多任务学习方法——多门混合专家模型(MMoE)，它可以从数据中显式地学习模型任务关系。通过合成数据的控制实验表明，所提出的方法可以更好地处理任务相关性较低的场景。通过对基准数据集和一个实际的大规模推荐系统的实验，本文证明了该方法在几种最先进的基线多任务学习模型上的成功。
此外，MMoE模型在很大程度上保留了计算优势，因为门控网络通常是轻量级的，并且专家网络在所有任务中都是共享的。如果模型通过使门控网络成为一个稀疏的Top-K门，有可能实现更好的计算效率。