SEAL：RLWE-BFV 开源算法库

参考文献：

1. GitHub - microsoft/SEAL: Microsoft SEAL is an easy-to-use and powerful homomorphic encryption library.
2. [NL11] Naehrig M, Lauter K, Vaikuntanathan V. Can homomorphic encryption be practical?[C]//Proceedings of the 3rd ACM workshop on Cloud computing security workshop. 2011: 113-124.
3. [GC15] Geihs M, Cabarcas D. Efficient integer encoding for homomorphic encryption via ring isomorphisms[C]//Progress in Cryptology-LATINCRYPT 2014: Third International Conference on Cryptology and Information Security in Latin America Florianópolis, Brazil, September 17–19, 2014 Revised Selected Papers 3. Springer International Publishing, 2015: 48-63.
4. [DGL+15] Dowlin N, Gilad-Bachrach R, Laine K, et al. Manual for using homomorphic encryption for bioinformatics[J]. 2015.
5. [CLP17] Chen H, Laine K, Player R. Simple encrypted arithmetic library-SEAL v2. 1[C]//Financial Cryptography and Data Security: FC 2017 International Workshops, WAHC, BITCOIN, VOTING, WTSC, and TA, Sliema, Malta, April 7, 2017, Revised Selected Papers 21. Springer International Publishing, 2017: 3-18.
6. [Alb15] Martin R. Albrecht, Rachel Player, and Sam Scott. On the concrete hardness of learning with errors. J. Mathematical Cryptology,9(3):169–203, 2015.
7. [HS13] Halevi S, Shoup V. Design and implementation of a homomorphic-encryption library[J]. IBM Research (Manuscript), 2013, 6(12-15): 8-36.

SEAL 算法库

BFV 变体

微软 [DGL+15] 给出了 BFV 的简单实现 SEAL（Simple Encrypted Arithmetic Library），之后的 [CLP17] 描述了 SEAL v2.1 版本。

SEAL 认为 BFV 的重线性化太慢了，因此它的同态乘法忽略了重线性化操作，仅在必要时才手动降低密文规模。

分园多项式环 $R=\mathbb{Z}[x]/(x^n+1)$，明文空间 $R_t$，密文空间 ${\bigcup }_{k\ge 2}{R}_t^k$

• 加密算法：将 $a(x)\in R_t$ 加密为向量 $ct=(c_0,c_1)$，满足
  $$\frac{q}{t}\cdot a\approx ct(s)=c_0+c_{1}s$$

• 同态加法：输入 $c{t}_1=(c_0,\cdots ,c_j)$ 和 $c{t}_2=(d_0,\cdots ,d_k)$，假设 $j\le k$，
  $$c{t}_{add}=([c_0+d_0{]}_q,\cdots ,[c_j+d_j{]}_q,d_{j+1},\cdots ,d_k)$$

• 同态乘法：输入 $c{t}_1=(c_0,\cdots ,c_j)$ 和 $c{t}_2=(d_0,\cdots ,d_k)$， $c{t}_{mult}=(C_0,\cdots ,C_{j+k})$，
  $$C_i={\left[\lfloor \frac{t}{q}\sum _{r+s=i}{c}_r{d}_s\rceil \right]}_q$$

• 解密算法：输入 $ct=(c_0,\cdots ,c_k)$，先计算
  $$ct(s)=\sum _i{c}_i{s}^i\in R_q$$
  再解码出 $a=[\lfloor t/q\cdot ct(s)\rceil {]}_t\in R_t$

另外，SEAL 扩展了 evaluation key 和 relinearization。假设把 $q$ 做 $w$ 进制展开为 $l+1$ 比特，以控制噪声增长。采样 $a_{ji}\leftarrow R_q,e_{ji}\leftarrow \chi$，分别加密 $s^j,\forall j\ge 2$，
$$ev{k}_j=[(w^0{s}^j-(a_{j,0}s+e_{j,0}),a_{j,0}),\cdots ,(w^l{s}^j-(a_{j,l}s+e_{j,l}),a_{j,l})]$$

给定 $ev{k}_2,\cdots ,ev{k}_k$，输入 $ct=(c_0,\cdots ,c_k)$，令 $c_k^{(i)}$ 是它的 $w$ 进制分解，可以计算同态数乘
$$\begin{gathered} c_0^{\prime }=c_0+\sum _{i=0}^{l}ev{k}_k[i][0]\cdot c_k^{(i)} \\ {c}_1^{\prime }=c_1+\sum _{i=0}^{l}ev{k}_k[i][1]\cdot c_k^{(i)} \\ {c}_j^{\prime }=c_j,\forall 2\le j\le k-1 \end{gathered}$$

得到 $c{t}^{\prime }=(c_0^{\prime },\cdots ,c_{k-1}^{\prime })$，迭代多次回到 $c{t}^{\prime \prime }=(c_0^{\prime \prime },c_1^{\prime \prime })$

参数选取

[HS13] 给出了 BGV 的代码实现 HElib，但是并没有给出最佳参数选取，需要经过实机测试。[CLP17] 给出了一些参数选取的思路：

1. 密文模数 $q$ 形如 $2^A-B$（伪梅森素数），其中 $B$ 是绝对值很小的整数。此时，存在快速的模约简算法。
2. 满足 $2n|q-1$，从而可以使用 NTT 计算密文多项式的乘法。
3. 满足 $t|q-1$，此时 $q=\Delta t+r_t(q)$ 中的余数 $r_t(q)=1$ 很小，从而使得同态运算的噪声项 $poly(e_1,e_2,r_t(q))$ 更小一些。

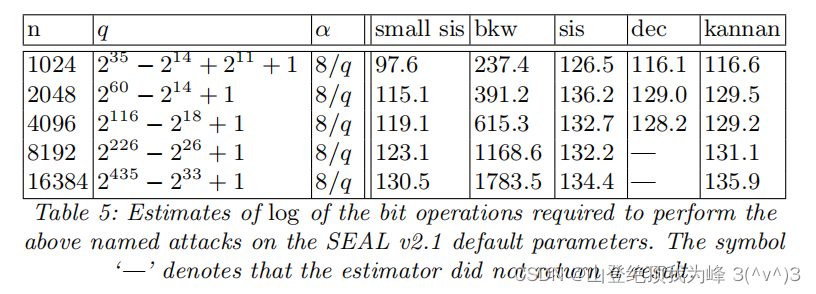
高斯噪声的标准差 $\sigma =3.19$，此时的高斯宽度 $\alpha q=\sigma \sqrt{2\pi }\approx 8$

[Alb15] 提出了针对 “short secret” LWE 的一种新型 BKW-style dual-lattice attack，将 HElib 和 SEAL 的安全强度降低了大约 $20$ 比特。在 [APS15] 中实现的 LWE estimator 集成了这种攻击。

SEAL v2.1 的参数选取 $(n,q,\alpha )$ 以及安全强度：

SEAL 的编码算法

由于 BFV 计算的是多项式的加法/乘法，我们希望把数值（int, float, bool）编码为多项式，并且保持同态性质。于是，我们需要同态的编码方案：只要不越界 $t$ 和 $x^n+1$，那么就可以正确解码。

Scalar Encoder

给定整数 $a\in \mathbb{Z}$，编码为常数多项式 $a(x)=a\in R_t$，只要同态运算过程中不越界 $t$ 那么解码正确

对于布尔值 b ∈ { 0 , 1 } b \in \{0,1\} b∈{0,1}，我们设置 $t=2$，于是 $b(x)=b\in R_2$，运算过程中自动模掉 $2$

为了高效计算 XOR、AND，也可以选取 $2n|t-1$，从而 $R_t\cong GF(t{)}^n$，以 CRT/SIMD 形式并行。

Integer Encoder

但是 Scalar Encoder 实在太浪费了，SEAL 提出可以把整数分解后编码到多项式上。并且分解后的系数较小，也不太容易越过 $t$ 导致溢出。

对于 $w=2$ 分解，$n+1$ 比特的带符号整数 $a=(-1{)}^{a_n}\cdot {\sum }_{i=0}^{n-1}{a}_i{2}^i$，编码函数为：
$$a(x)=(-1{)}^{a_n}\cdot \sum _{i=0}^{n-1}{a}_i{x}^i(\mathrm{mod}{x}^n+1,t)$$

易知，解码函数就是 $a=a(2)$ 是多项式求值。于是有：

• 整数加法 $a+b⟺a(x)+b(x)(\mathrm{mod}{x}^n+1,t)$，它的系数是在 $\mathbb{Z}$ 上的，但是用 ${\mathbb{Z}}_t$ 来模拟。
• 整数乘法 $a\cdot b⟺a(x)\cdot b(x)(\mathrm{mod}{x}^n+1,t)$，它的多项式是在 $\mathbb{Z}[x]$ 上的，但是用 ${\mathbb{Z}}_t[x]/(x^n+1)$ 模拟。
• 整数 XOR 也是容易的，但是整数 AND 无法计算。

对于 $w\ge 3$，采取 balanced base-$w$ representation，多项式每个系数的范围是 { − ⌊ w / 2 ⌋ , ⋯   , 0 , ⋯ ⌊ w / 2 ⌋ } \{-\lfloor w/2\rfloor,\cdots,0,\cdots\lfloor w/2\rfloor\} {−⌊w/2⌋,⋯,0,⋯⌊w/2⌋}，这使得同态运算时的系数增长的没那么快。

Fractional Encoder

对于有限精度的实数 $a\in \mathbb{R}$，我们可以采用 Scale + Integer Encoder 的方式，形如 $(a(x),\delta )$，但是同态计算时需要追踪 scale 的变化，并且不同 scale 之间做运算还需要转换。

SEAL 提出了另一种编码器。有限精度实数 $a=a^{+}.a^{-}$，

• 整数部分：$a^{+}=a_{n_i}{a}_{n_i-1}\cdots a_0$
• 小数部分：$a^{-}=a_{-1}\cdots a_{-n_f}$
• 符号位 $a_{n_i}^{+}$，整数部分的精度为 $n_i$，小数部分的精度为 $n_f$

编码函数为：
$$a(x)=(-1{)}^{a_{n_i}^{+}}\cdot \left(\sum _{i=0}^{n_i-1}{a}_i^{+}{x}^i-\sum _{i=0}^{n_f-1}{a}_i^{-}{x}^{n-i}\right)(\mathrm{mod}{x}^n+1,t)$$

由于 $(\mathrm{mod}{x}^n+1)$，因此小数部分的 Integer Encoder 带有负号。容易验证，$a+b⟺a(x)+b(x)$，$ab⟺a(x)b(x)$，只要不越过边界 $x^n+1$ 和 $t$。我们需要设置 $n_i+n_f\le n-1$，保证整数部分和小数部分不重叠。

如果在同态运算过程中，小数部分的 LSB 被消除（系数是 $0$）、整数部分的 MSB 被消除（系数是 $0$），那么对应的精度 $n_i,n_f$ 也会相应缩小。比较 Scale + Integer Encoder，它的 Scale 不断增长，很容易越过 $x^n+1$ 导致溢出。