214. Devu和鲜花

214. Devu和鲜花 - AcWing题库

如果每个盒子里的花的数量是无限的，用隔板法可以得出答案是 

现在每个盒子中区的花数要满足n个条件

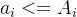
我们可以求答案的补集，用全部方案数减去补集方案数

每一个不符合条件的要求为，设为Bi

补集方案数为就成了一个容斥原理

对于一个不符合要求的是，这就相当于先把ai+1个减了再用隔板法

多个以此类推

#include
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'
 
using namespace std;
 
typedef pair<int, int> PII;
typedef long long ll;
typedef long double ld;
 
const int N = 30, mod = 1e9 + 7;
 
ll n, m;
ll A[N];
int down = 1;
 
int qmi(int a, int k)
{
	int res = 1;
	while(k)
	{
		if(k & 1)res = (ll)res * a % mod;
		a = (ll)a * a % mod;
		k >>= 1;
	}
	return res;
}
 
int C(ll a, ll b)
{
	if(a < b)return 0;
	
	ll up = 1;
	for(ll i = a; i > a - b; i --)
		up = i % mod * up % mod;
	
	return up * down % mod;
}
 
int main()
{
	IOS
	cin >> n >> m;
	for(int i = 0; i < n; i ++)cin >> A[i];
	
	for(int i = 2; i <= n - 1; i ++)
		down = (ll)down * i % mod;
	down = qmi(down, mod - 2);
	
	int num = 1 << n;
	ll ans = 0;
	for(int i = 0; i < num; i ++)
	{
		ll a = m + n - 1, b = n - 1;
		int cnt = 0;
		for(int j = 0; j < n; j ++)
		{
			if(i >> j & 1)
			{
				a -= A[j] + 1;
				cnt ++;
			}
		}
		if(cnt & 1)ans = (ans - C(a, b)) % mod;
		else ans = (ans + C(a, b)) % mod;
	}
	
	cout << (ans + mod) % mod;
	
	
	return 0;
}