交叉熵损失函数

引言

• 本文只是对自己理解交叉熵损失函数的一个总结，并非详尽介绍交叉熵函数的前世今生，要想多方位了解该损失函数，可以参考本文参考资料。

(1)交叉熵损失函数表达式的推导

• 单个样本的表达式为：
  $$L=-[y\log \hat{y}+(1-y)\log (1-\hat{y})]\text{\hspace{1em}(1)}$$
• 在二分类问题模型：例如逻辑回归「Logistic Regression」、神经网络「Neural Network」等，真实样本的标签为 [0，1]，分别表示负类和正类。模型的最后通常会经过一个 Sigmoid 函数，输出一个概率值，这个概率值反映了预测为正类的可能性：概率越大，可能性越大。
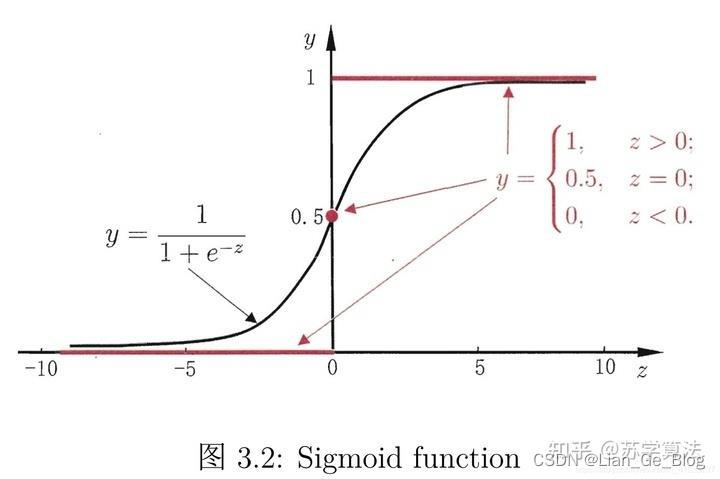
• Sigmoid 函数的表达式和图形如下所示：
  $$g(s)=\frac{1}{1+e^{-s}}\text{\hspace{1em}(2)}$$
  
• 其中 s 是模型上一层的输出，Sigmoid 函数有这样的特点：s = 0 时，g(s) = 0.5；s >> 0 时， g ≈ 1，s << 0 时，g ≈ 0。显然，g(s) 将前一级的线性输出映射到 [0，1] 之间的数值概率上。这里的 g(s) 就是交叉熵公式中的模型预测输出 (“s 是模型上一层的输出”在下方有注释)。
• 如果说预测输出即 Sigmoid 函数的输出表征了当前样本标签为 1 的概率：
  $$\hat{y}=P(y=1|x)\text{\hspace{1em}(3.1)}$$
• 那么很明显，当前样本标签为 0 的概率就可以表达成：
  $$1-\hat{y}=P(y=0|x)\text{\hspace{1em}(3.2)}$$
• 如果我们综合一下两种情况表达式就为：
  $$P(y|x)={\hat{y}}^y\ast (1-\hat{y}{)}^{1-y}\text{\hspace{1em}(3.3)}$$
• 整合后的表达式，不管是y=0或者1，我们都希望P（y|x）的值越大越好，因为不管标签是0还是1，概率值越大都说明该样本更应该归属于哪一类，那么如何求解呢？
  • 使用极大似然的思想，首先引入log函数，保证函数单调性不变，那么根据log函数的单调性，想要P（y|x）越大，那么可以让-P（y|x）越小，其实就是说，让其概率值更大，反方向理解就是损失更小才能作为损失函数来用，那么交叉熵损失函数就是多个样本损失函数的和，N个样本的和就是：
    $$L=-\sum _{i=1}^N(y_i\log {\hat{y}}_i+(1-y_i)\log {(1-\hat{y}}_i))\text{\hspace{1em}(4)}$$
• 再从交叉熵损失函数的图像来理解(单个样本损失函数)
  
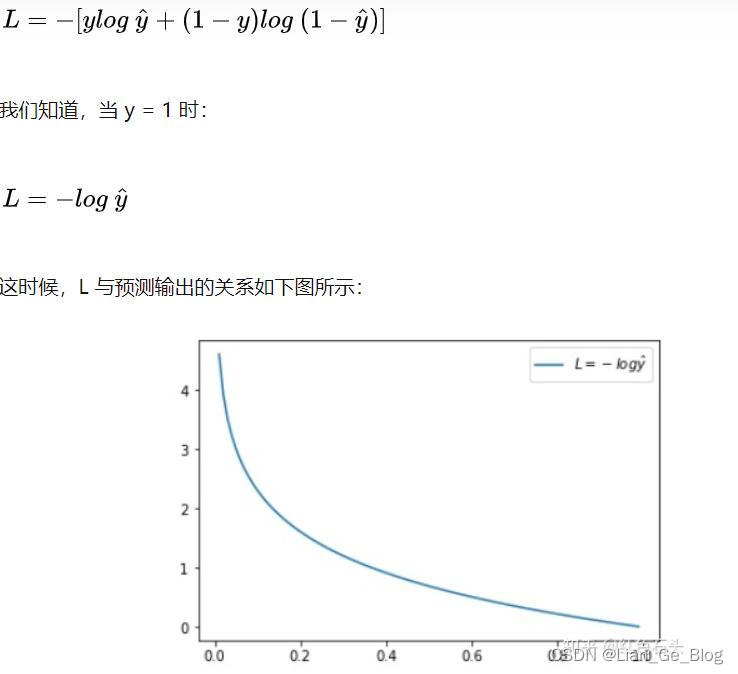
• 横坐标是预测输出，纵坐标是交叉熵损失函数 L。显然，预测输出越接近真实样本标签 1，损失函数 L 越小；预测输出越接近 0，L 越大

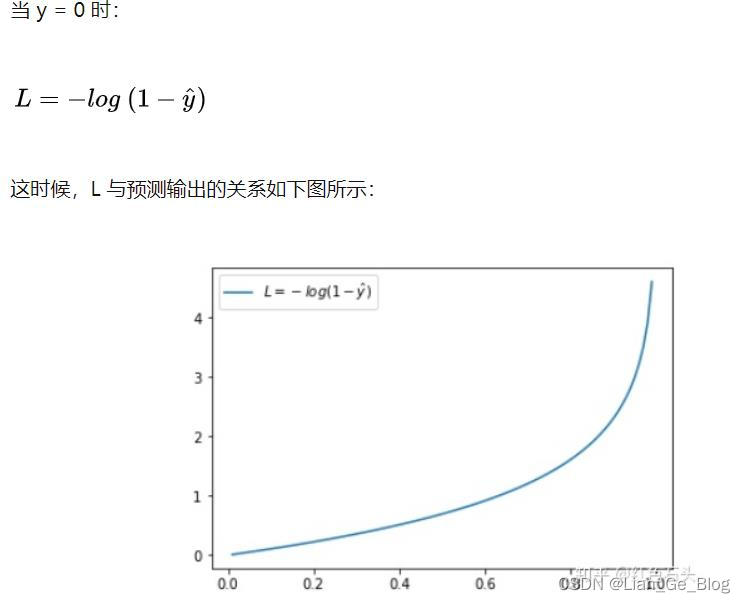
• 预测输出越接近真实样本标签 0，损失函数 L 越小；预测函数越接近 1，L 越大

关于分类问题的损失函数常用交叉熵损失函数，而非均方误差MSE

从两者表达式来看

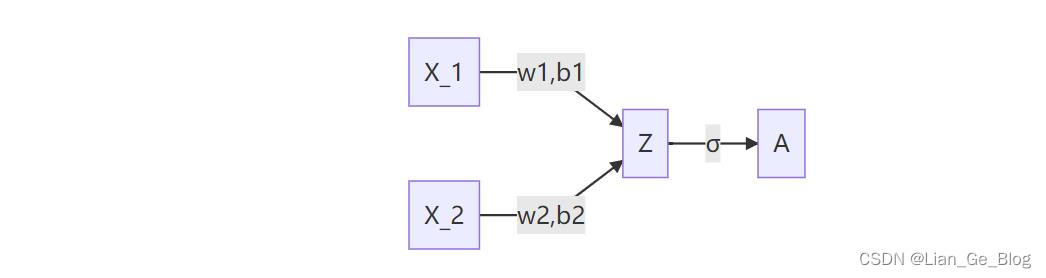
• 便于理解，我们用上图做一个简单的推导$$Z（x）=w\ast b，A（z）=\sigma （z）=\frac{1}{1+e^{-z}}\text{\hspace{1em}(5)}$$
• 那么MSE损失表达式就是：(A为分类结果的概率值，y为真实分类值，即0或者1)$$C=\frac{(A-y{)}^2}{2}\text{\hspace{1em}(6)}$$
• 使用梯度下降法的更新w和b时，对w和b进行求导$$\frac{\partial C}{\partial w}=\frac{\partial C}{\partial A}\frac{\partial A}{\partial Z}\frac{\partial Z}{\partial w}=(A-y){\sigma }^{\prime }(Z)x=(A-y)A(1-A)x\approx A{\sigma }^{\prime }(z)\text{\hspace{1em}(7)}$$
• 同理对b求导$$\frac{\partial C}{\partial b}=\frac{\partial C}{\partial A}\frac{\partial A}{\partial Z}\frac{\partial Z}{\partial b}=(A-y){\sigma }^{\prime }(Z)=(A-y)A(1-A)\approx A{\sigma }^{\prime }(z)\text{\hspace{1em}(8)}$$
• 注：由于输入数据时形式为xi yi，所以为已知量，所以约等于得时候将x和y略去
• 注:在(7) (8)中σ’(z) = σ(z) * （1 - σ(z)）的推导如下，其也是sigmoid函数的基本性质
• 
• 注：该基本性质可以在很多场景下用到
• 更新后的w和b：$$w=w-\eta \frac{\partial C}{\partial w}=w-\eta A{\sigma }^{\prime }(z)\text{\hspace{1em}(9)}$$ $$b=b-\eta \frac{\partial C}{\partial b}=b-\eta A{\sigma }^{\prime }(z)\text{\hspace{1em}(10)}$$
• 因为sigmoid函数的性质，如图的两端，几近于平坦，导致σ’(z)在z取大部分值得时候会很小，那么就会导致w和b更新很慢，定量解释可以下图
• 这就带来实际操作的问题。当梯度很小的时候，应该减小步长（否则容易在最优解附近产生来回震荡），但是如果采用 MSE ，当梯度很小的时候，无法知道是离目标很远还是已经在目标附近了。（离目标很近和离目标很远，其梯度都很小）
  
  

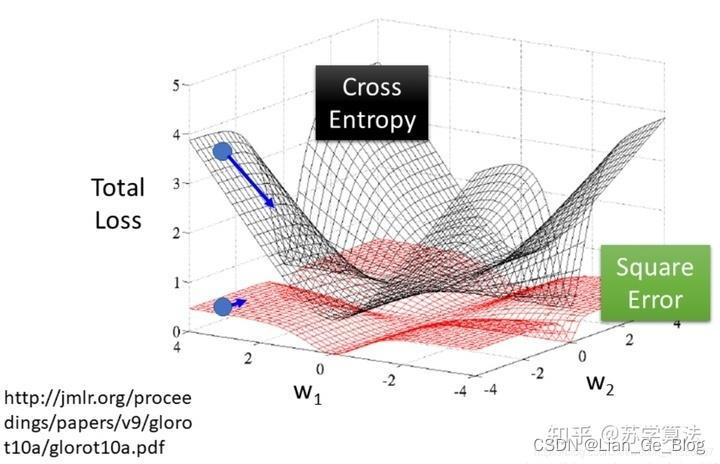
为了克服上述 MSE 不足，引入了categorical_crossentropy（交叉熵损失函数）

• 交叉熵损失函数同理推导，其中交叉熵误差表达公式为：（其实需要累加，此处方便理解就不累加了）$$L=-（y\ast ln(a)+(1-y)\ast ln(1-a)）\text{\hspace{1em}(11)}$$
• 推导过程如下：(推导过程可以参考上面mse损失推导过程,(5)依旧可用,求偏导的步骤可以参考(7)) $$\frac{\partial L}{\partial w}=(-\frac{y}{a}+\frac{1-y}{1-a})x{\sigma }^{\prime }(z)\text{\hspace{1em}(12)}$$
• 注：σ’(z) = σ(z) * （1 - σ(z)） = a * (1 - a)，推导过程如上图手写部分$$\frac{\partial L}{\partial w}=(ay-y+a-ay)x=(a-y)x\text{\hspace{1em}(13)}$$
• 注：w的更新中没有了导数σ’(z),只跟(a-y)有关，也就是真实值和输出值的误差，那么误差大的时候更新就快，误差小的时候更新就慢

从优化问题看

• MSE是非凸优化问题，而交叉熵是凸优化问题
• MSE

• 交叉熵损失函数：
  
  
  
  
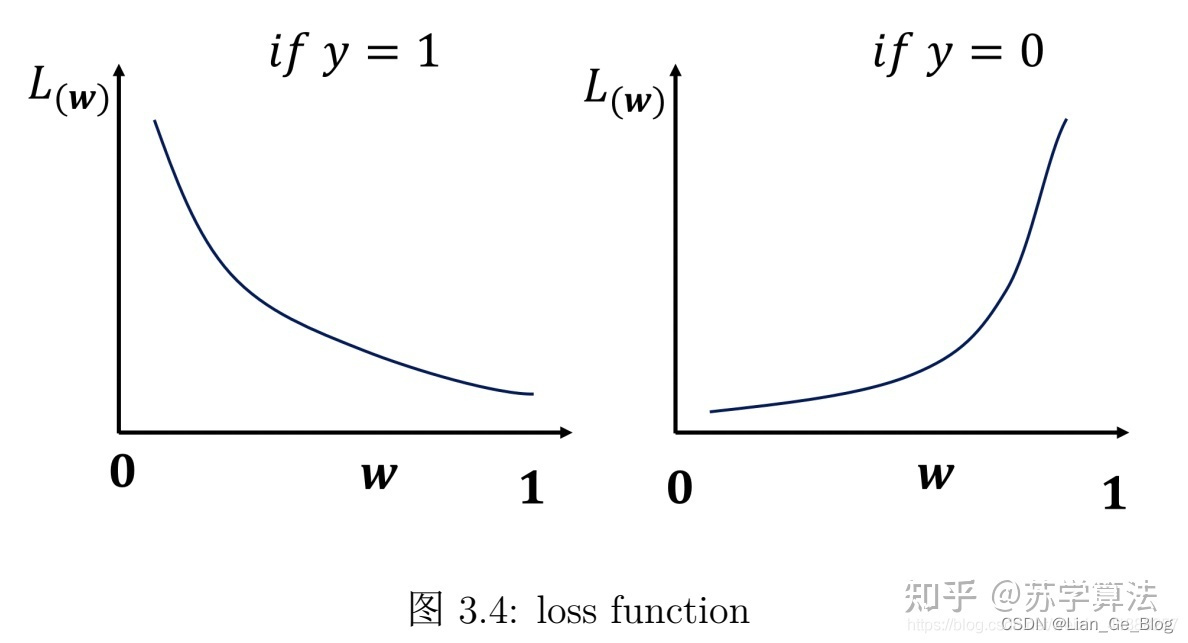
• 当类别标签为y=1 时，越靠近 1 则损失越小；当类别标签为 y=0时，越靠近 1 则损失越大.

参考资料

• 关于分类问题的损失函数使用交叉熵损失函数的原因以及公式推导参考资料(参考资料可以比对推导过程更容易理解一些)
  • 1 为什么分类问题的损失函数采用交叉熵而不是均方误差MSE？ - 知乎 (zhihu.com)
  • 2 交叉熵损失(Cross-entropy)和平方损失(MSE)究竟有何区别？ - 知乎 (zhihu.com)
  • 3 极大似然估计原理_呆呆象呆呆的博客-CSDN博客_极大似然估计的原理
• 关于交叉熵的交叉和熵的概念参考：
  1 一文搞懂熵(Entropy),交叉熵(Cross-Entropy) - 知乎 (zhihu.com)
• 关于多个方法推导交叉熵损失函数可以参考
  1 简单的交叉熵损失函数，你真的懂了吗？ - 知乎 (zhihu.com)
• 例子较多的参考：
  1 损失函数｜交叉熵损失函数 - 知乎 (zhihu.com)