MATLAB神经网络和优化算法

1. matlab感知器神经网络初步学习

%%   学习目标：从学习第一个最简单的神经网络案例开启学习之路
%%   感知器神经网络   用于点的分类
clear all;
close all;
P=[0 0 1 1;0 1 0 1];                         %输入向量
T=[0 1 1 1];                                 %目标向量
net=newp(minmax(P),1,'hardlim','learnp');    %建立感知器神经网络
net=train(net,P,T);                          %对网络进行训练
Y=sim(net,P);                                %对网络进行仿真
plotpv(P,T);                                 %绘制感知器的输入向量和目标向量，绘制样本点
plotpc(net.iw{1,1},net.b{1});                %在感知器向量图中绘制分界线

1
2
3
4
5
6
7
8
9
10
11
12
13

运行结果：

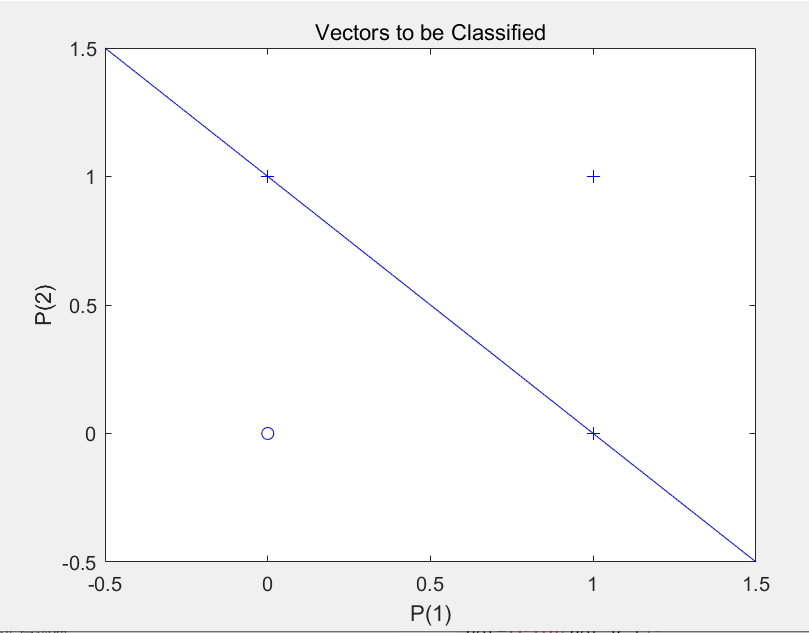
网络图：

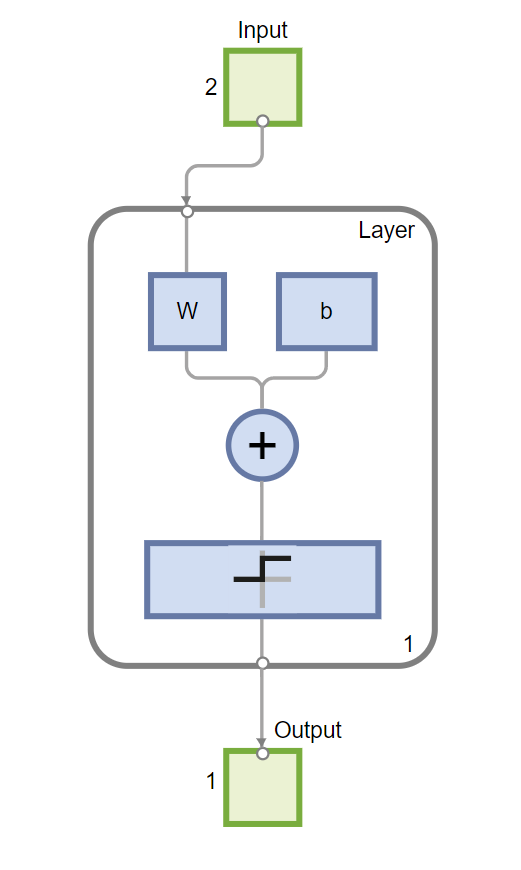
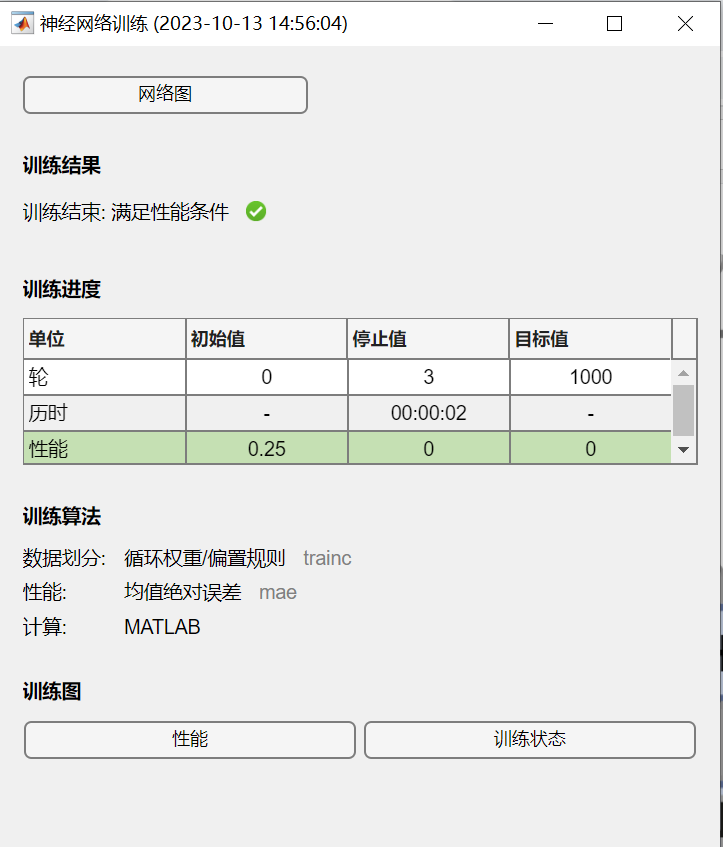
2 使用建立好的神经网络进行分类程序

clear all;
close all;
P=[-0.4 -0.4 0.5 -0.2 -0.7;-0.6 0.6 -0.4 0.3 0.8];      %输入向量
T=[1 1 0 0 1];                                          %输出向量
plotpv(P,T);                                            %绘制样本
net=newp(minmax(P),1,'hardlim','learnpn');              %建立神经网络
hold on;
linehandle=plot(net.IW{1},net.b{1});
E=1;
net.adaptParam.passes=10;
while mae(E)                                            %误差达到要求才停止训练
    [net,Y,E]=adapt(net,P,T);                           %进行感知器神经网络的训练
    linehandle=plotpc(net.IW{1},net.b{1},linehandle);
    drawnow;
end
save net1 net;                                          %将训练好的神经网络进行保存
set(gcf,'position',[60,60,300,300]);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

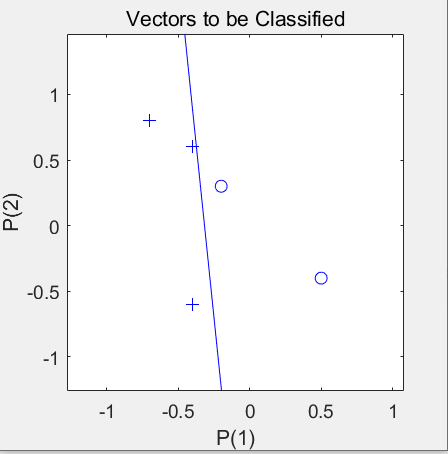
%%  用刚才建立的神经网络进行分类
clear all;
close all;
load net1.mat;                                  %加载上次训练好的神经网络
X=[-0.3 0.3 0.9;-0.6 0.2 0.8];                  %输入向量
Y=sim(net,X);                                   %对输入进行仿真
figure;
plotpv(X,Y);                                    %绘制样本点
plotpc(net.IW{1},net.b{1});                     %绘制分类线
set(gcf,'position',[60,60,300,300]);
1
2
3
4
5
6
7
8
9
10

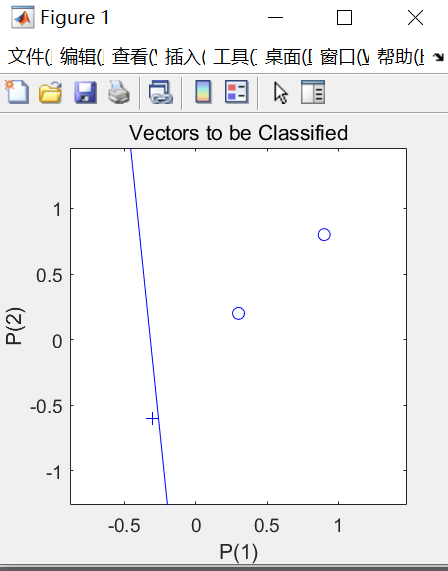
3 线性神经网络预测程序

%% 学习目标： 线性神经网络
%%  收敛速度和精度比之前讲的感知器神经网络要高，
%%  主要应用在函数逼近，信号预测，模式识别，系统辨识方面
clear all;
close all;
P=[1.1 2.2 3.1 4.1];
T=[2.2 4.02 5.8 8.1];
lr=maxlinlr(P);                   %获取最大学习速率
net=newlin(minmax(P),1,0,lr);     %建立线性神经网络
net.trainParam.epochs=500;        %训练    做多500次
net.trainParam.goal=0.04;         %训练误差设定为0.04
net=train(net,P,T);
Y=sim(net,P)                       %仿真
1
2
3
4
5
6
7
8
9
10
11
12
13

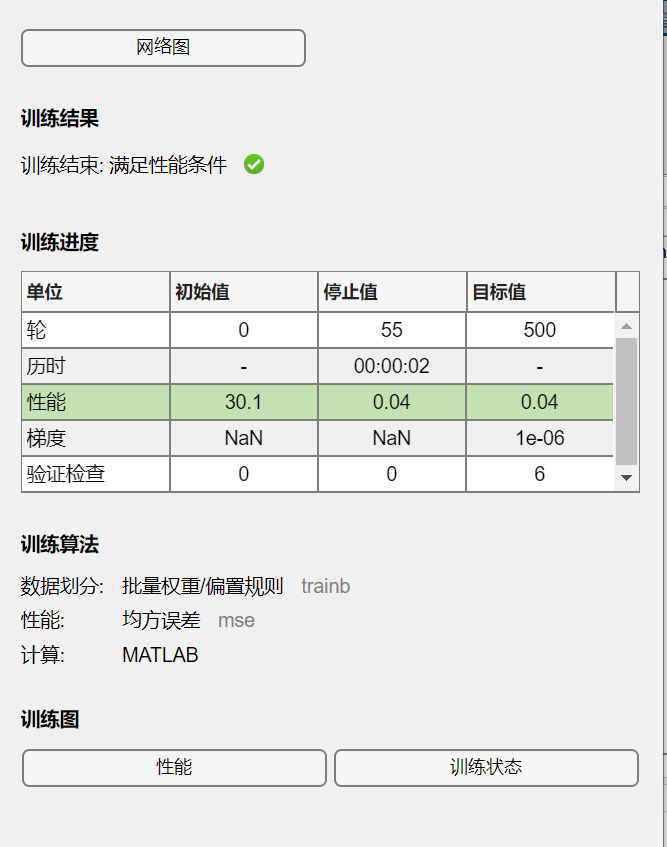
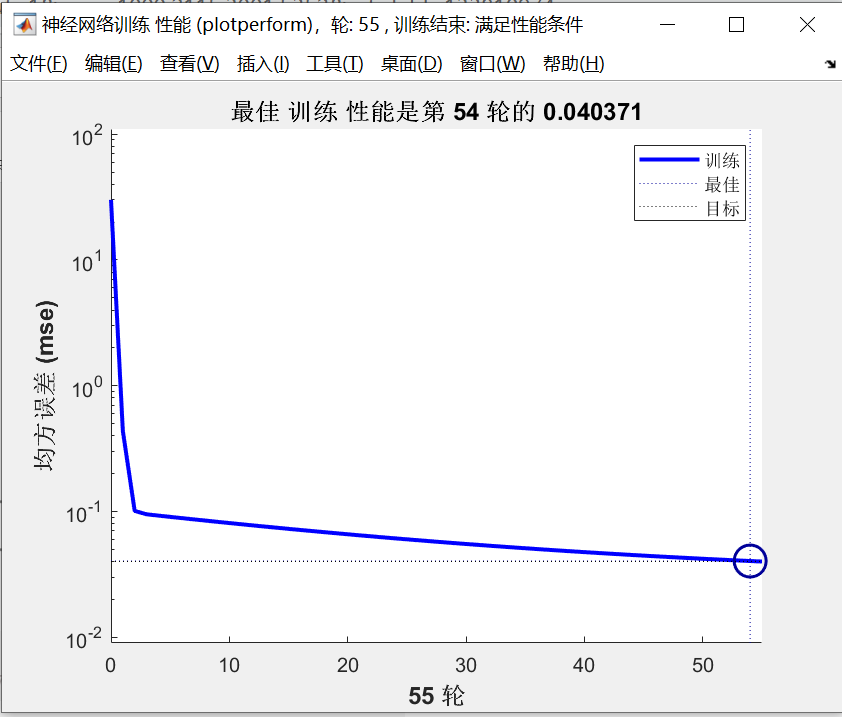
%%  利用线性神经网络进行信号的预测
clear all;
close all;
t=0:pi/10:4*pi;
X=t.*sin(t);
T=2*X+3;
figure;
plot(t,X,'+-',t,T,'+--');
legend('系统输入','系统输出');
set(gca,'xlim',[0 4*pi]);
set(gcf,'position',[50,50,400,400]);
net=newlind(X,T);
y=sim(net,X);
figure;
plot(t,y,'+:',t,y-T,'r:');
legend('网络预测输出','误差');
set(gca,'xlim',[0 4*pi]);
set(gcf,'position',[50,50,400,400]);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

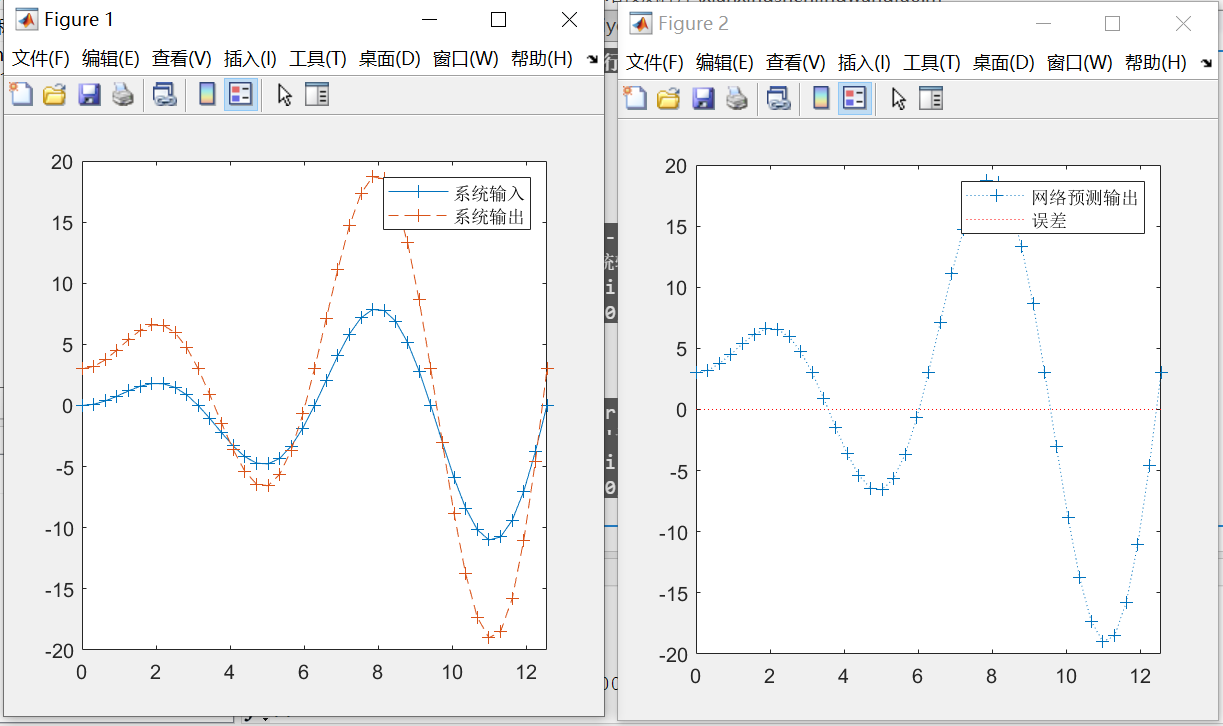
4 BP神经网络信号拟合程序

%%  学习目标：BP神经网络
%%  函数逼近  数据压缩   模式识别
%%  考虑要素：网络层数  输入层的节点数  输出层的节点数  隐含层的节点数
%%  传输函数  训练方法
%%  对信号曲线进行拟合
clear all;
clear all;
P=-1:0.04:1;
T=sin(2*pi*P)+0.1*randn(size(P));
net=newff(P,T,18,{},'trainbr');    %%   隐含层神经元个数是18
net.trainParam.show=10;
net.trainParam.epochs=100;         %%  训练100次
net=train(net,P,T);
Y=sim(net,P);
figure;
plot(P,T,'-',P,Y,'+');
legend('原始信号','网络输出信号');
set(gcf,'position',[20,20,500,400]);

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

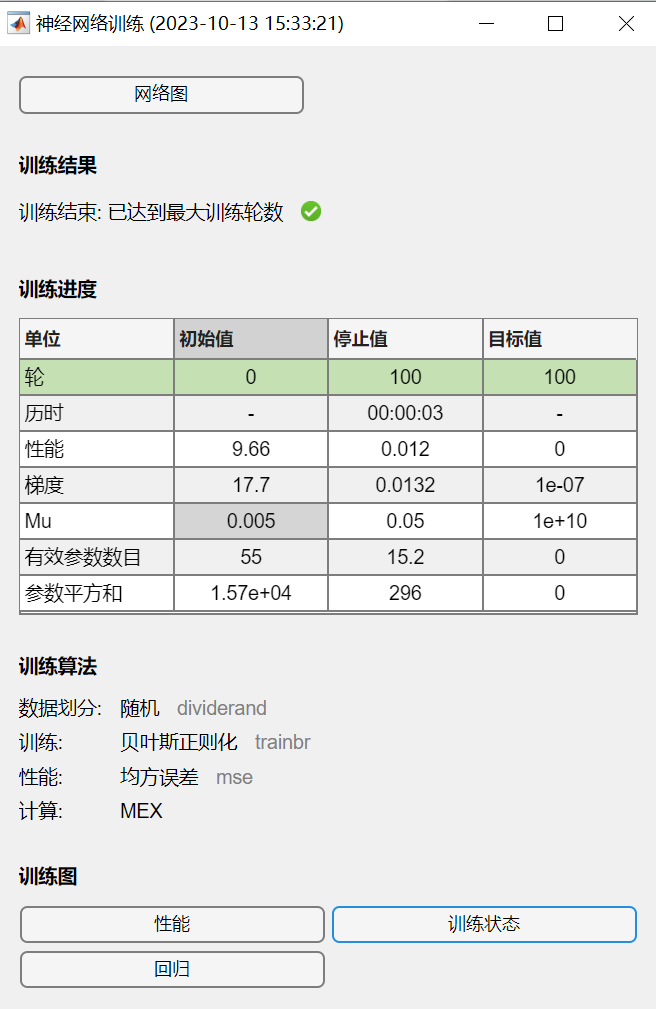
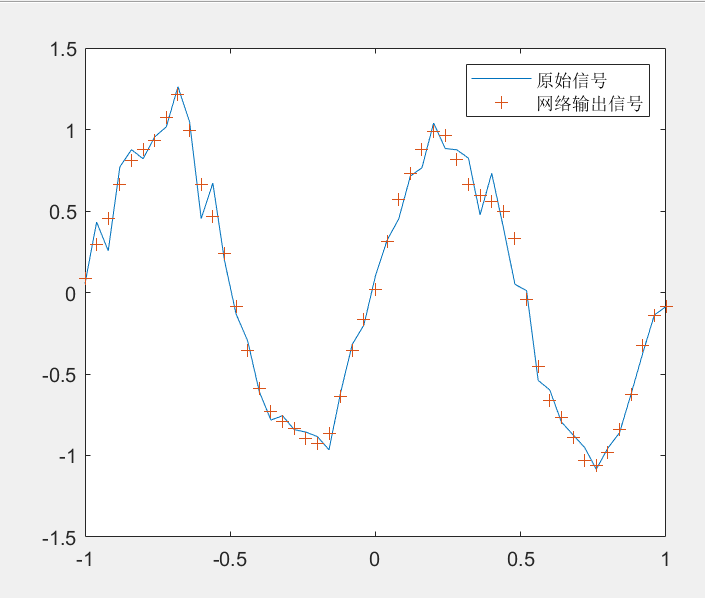
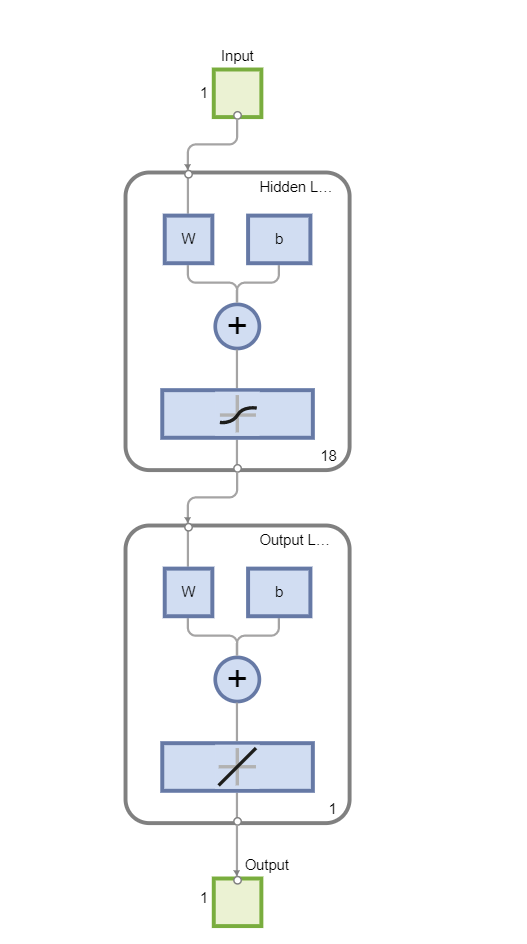
网络图：

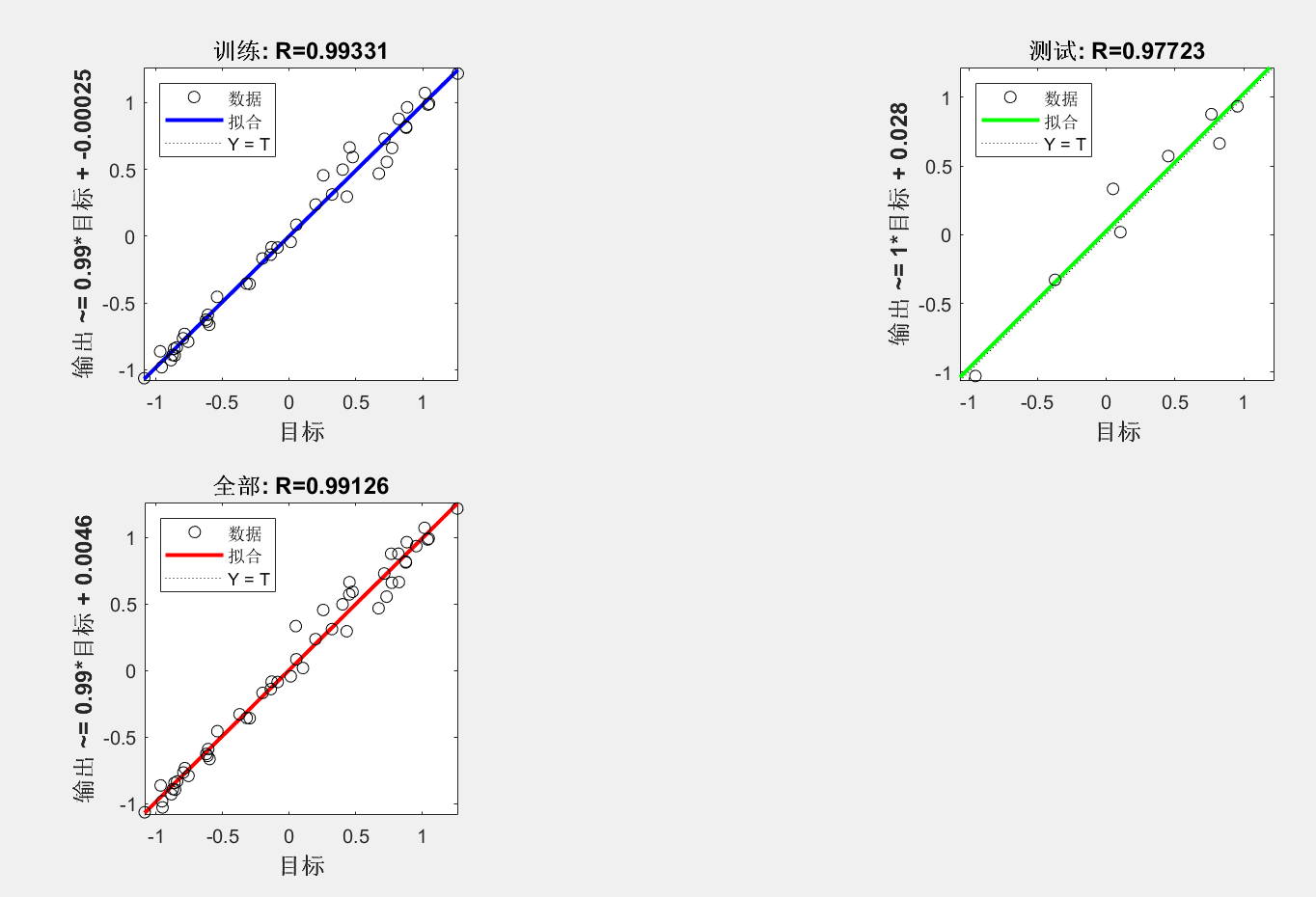
回归：

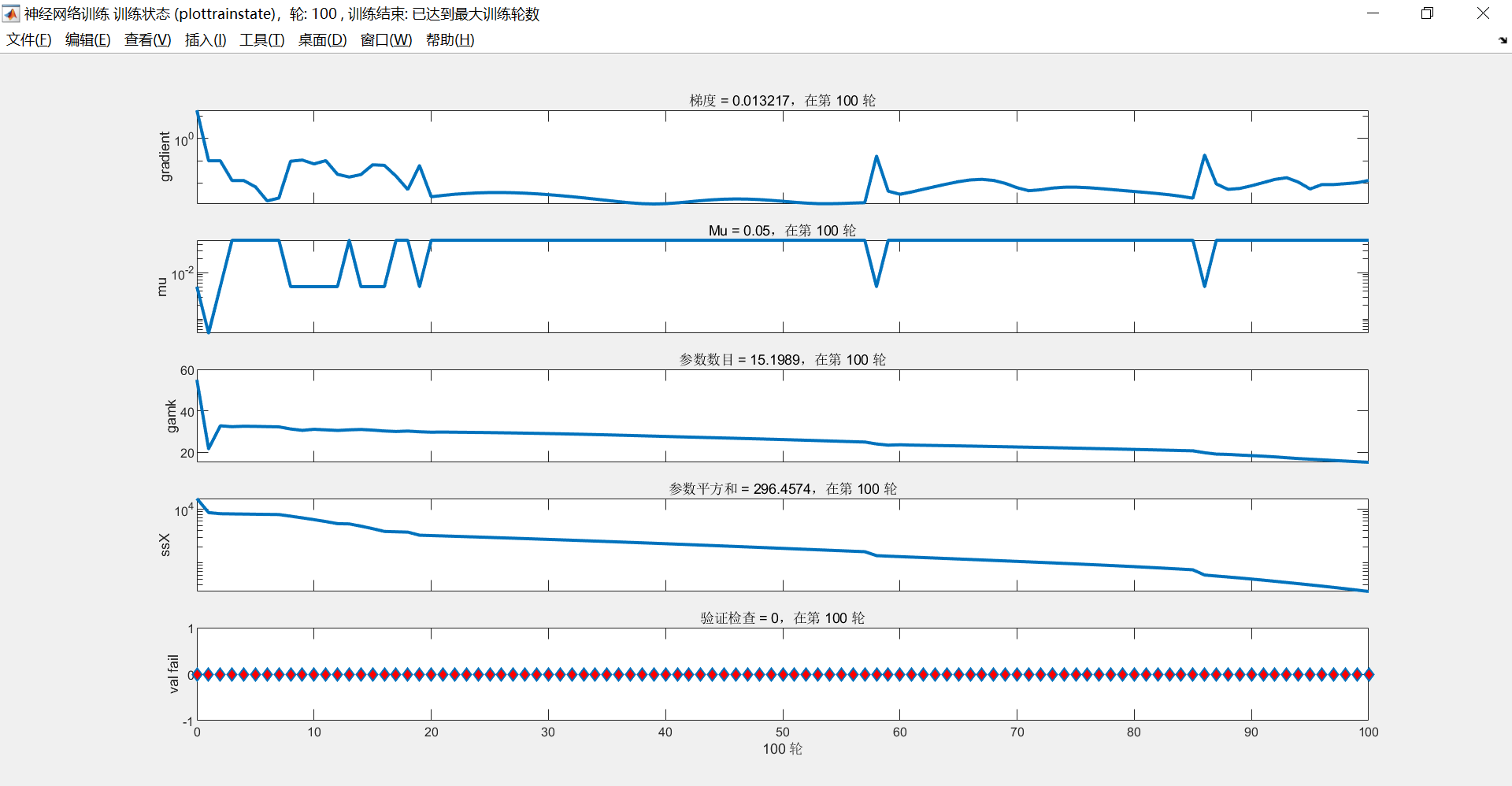
训练状态：