双目标定之张正友标定法数学原理详解matlab版

目录

前言

1.相机标定

1.1 双目视觉基本原理

1. 2 相机的四个坐标系

1.3 相机畸变与校正

2.1 相机标定

张正友友棋盘格标定法在matlab的实现

---

这一篇主要详细介绍标定原理和相机各个坐标系之间的关系为后续的定位测距和重建做基础

前言

最近重新整理了一下自己做过的双目项目，准备从零开始更新双目的相关知识

1.相机标定

相机标定是计算机视觉中的一个重要步骤，它用于确定相机内部参数和外部参数，以便准确地将二维图像坐标与三维世界坐标对应起来。

相机标定的目的是消除摄像机镜头畸变和确定相机的内部参数，包括焦距、主点位置和像素间距等。同时，还可以确定相机的外部参数，如相机的位置和朝向。

常用的相机标定方法有两种：基于标定板和基于特征点。

基于标定板的方法是使用已知尺寸和几何结构的平面标定板，通过拍摄不同位置和角度下的图像，推导出相机的内外参数。这种方法需要在标定板上布置一些特殊的标记点或者棋盘格，在图像中检测和识别这些点，进而进行标定。

基于特征点的方法是通过检测图像中的特征点（如角点、边缘点等），并与其对应的三维世界坐标建立映射关系，从而计算相机的内外参数。这种方法不需要特殊的标定板，只要能够提取到足够多的特征点就可以进行标定。

相机标定的结果可以用于各种计算机视觉任务，如目标检测、物体跟踪、三维重建等。它能够提高图像处理的精度和鲁棒性，使得计算机能够更准确地理解和处理图像数据。

1.1 双目视觉基本原理

相比于单目视觉系统，双目立体视觉系统可以得到图像的三维坐标信息，进而计算出目标物体的距离信息，且双目立体视觉系统的测量精度较高、效率较快，因而具有无可取代的优势。

双目立体视觉为减少像素匹配点的立体匹配运算过程，一般多借助平行于同一水平线的左右2个摄像头，从2个不同视角对同一时间、同一场景拍下一组图像，然后对左右图像中的特征匹配点进行匹配计算出图像的深度信息，建立图像的视差图，得到图像的三维坐标信息,最终根据公式转换得到实际距离，完成双目测距功能。双目立体视觉的基本原理如图1所示。

图1中，P(x,z)表示目标树种的位置坐标；P1(x1,f)表示左目图像中的目标树种投影点的位置坐标；P2(x2,f)表示右目图像中的目标树种投影点的位置坐标；f表示焦距；c1、c2分别表示左右两摄像头的光心；b表示两摄像头光心之间的距离，即基线，则三角关系式如式(1)所示。

                                                   

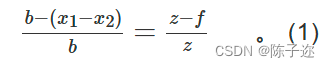
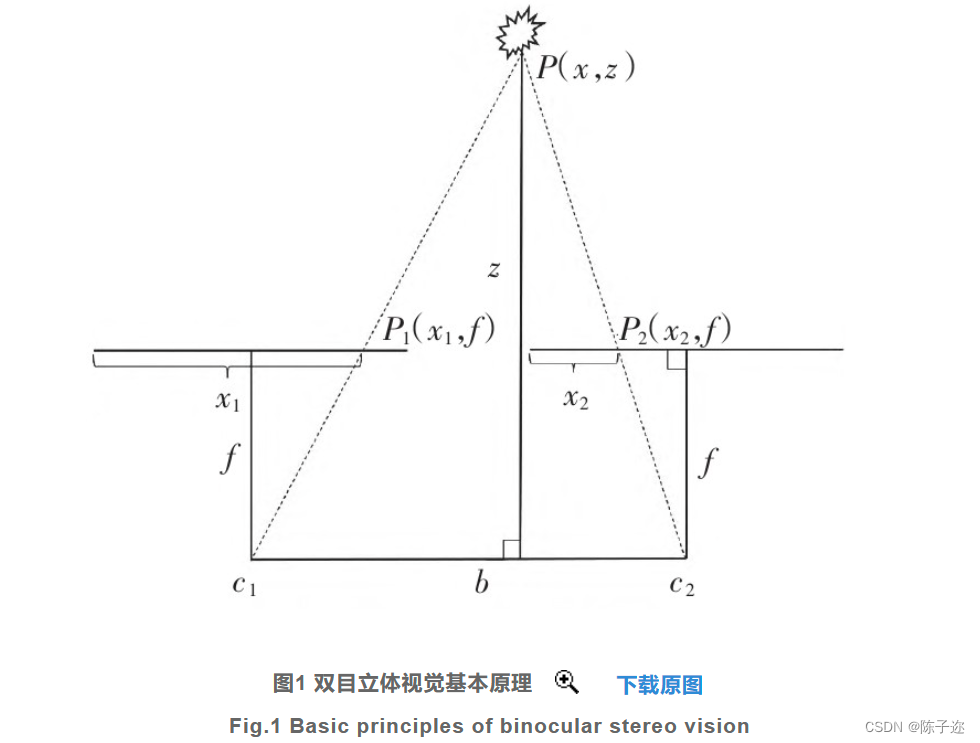
对三角关系式进行转换，即可得到所求距离z,如式(2)所示。

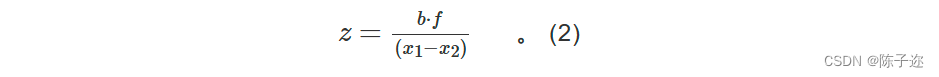
1. 2 相机的四个坐标系

相机成像系统中，共包含四个坐标系：世界坐标系、相机坐标系、图像坐标系、像素坐标系。对于这四个坐标系中之间的关系还不太明白成像原理的同学需要先查一查学习一下。

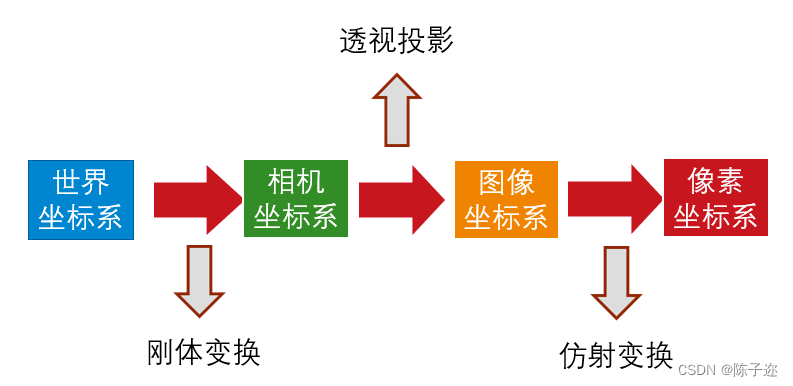
双目视觉模型如图1所示，使用世界坐标系(OwXwYwZw)、相机坐标系(OclXclYclZcl或OcrXcrYcrZcr)、图像坐标系(ODlXDlYDl或ODrXDrYDr)和像素坐标系(OlXlYl或OrXrYr)的相互变化来描述空间点到图像点的成像过程，世界坐标系中某一点P(X,Y,Z)在双目相机采集到的左右图像上的投影分别为Pl和Pr,OlOcl和OrOcr为分别为相机的成像平面与像素平面点的距离，即相机的焦距fl和fr。

由双目视觉模型可以得到4种坐标系的对应关系，其中世界坐标系(OwXwYwZw)下的坐标通过旋转矩阵R和平移向量T转换到相机坐标系(OclXclYclZcl)下的坐标表示，其关系式为

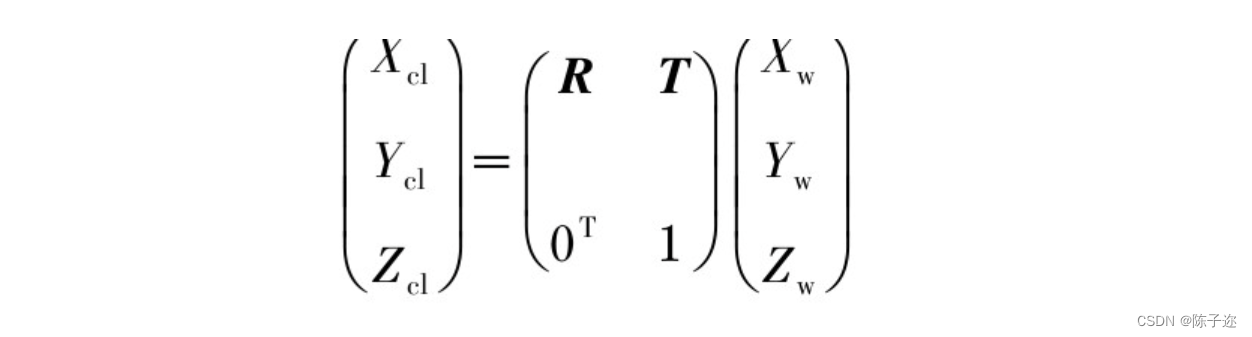
相机坐标系(OclXclYclZcl)下的坐标通过透视投影转换到图像坐标系(ODlXDlYDl)下的坐标，其关系式如式(2)所示，式(2)可以通过齐次变换为式(3)Xcl/f=Xcl/Zcl,Ycl/f=Ycl/Zcl   (2)

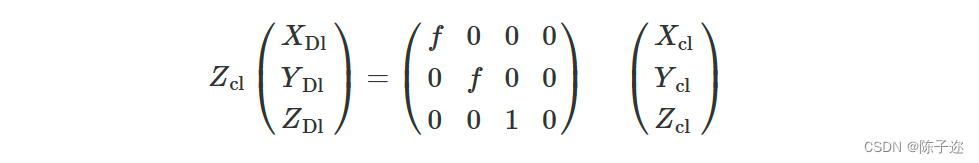
图像坐标系(ODlXDlYDl)下的坐标通过离散化转换到像素坐标系(OlXlYl)下的坐标，(ul,vl)表示像素坐标，单位为像素(pixel),其关系式为

将式(1)、式(3)和式(4)联立，可以确定世界坐标系(OwXwYwZw)和像素坐标系(OlXlYl)的关系为

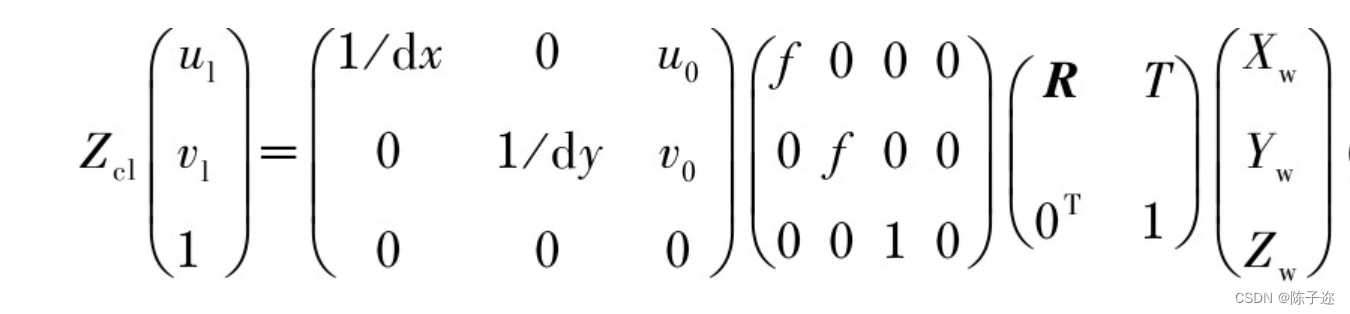
1.3 相机畸变与校正

在相机采集图像产生畸变包括径向畸变和切向畸变，径向畸变主要是相机镜头的形状造成的，调节公式为

由于制造上的缺陷使相机在组装过程中产生切向畸变，切向畸变用2个额外参数P1和P2表示，调节公式为 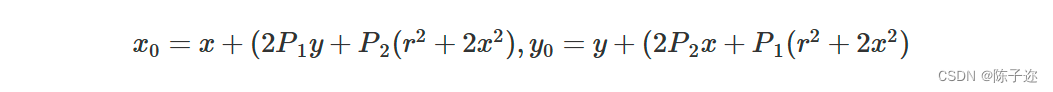采用Zhang Z Y[10]的棋盘标定法对双目相机标定

2.1 相机标定

张正友友棋盘格标定法在matlab的实现

打开Matlab 上方的工具栏APP，找到图像处理和计算机视觉下的Stereo Camera Calibration工具，打开并将分割后的图片导入

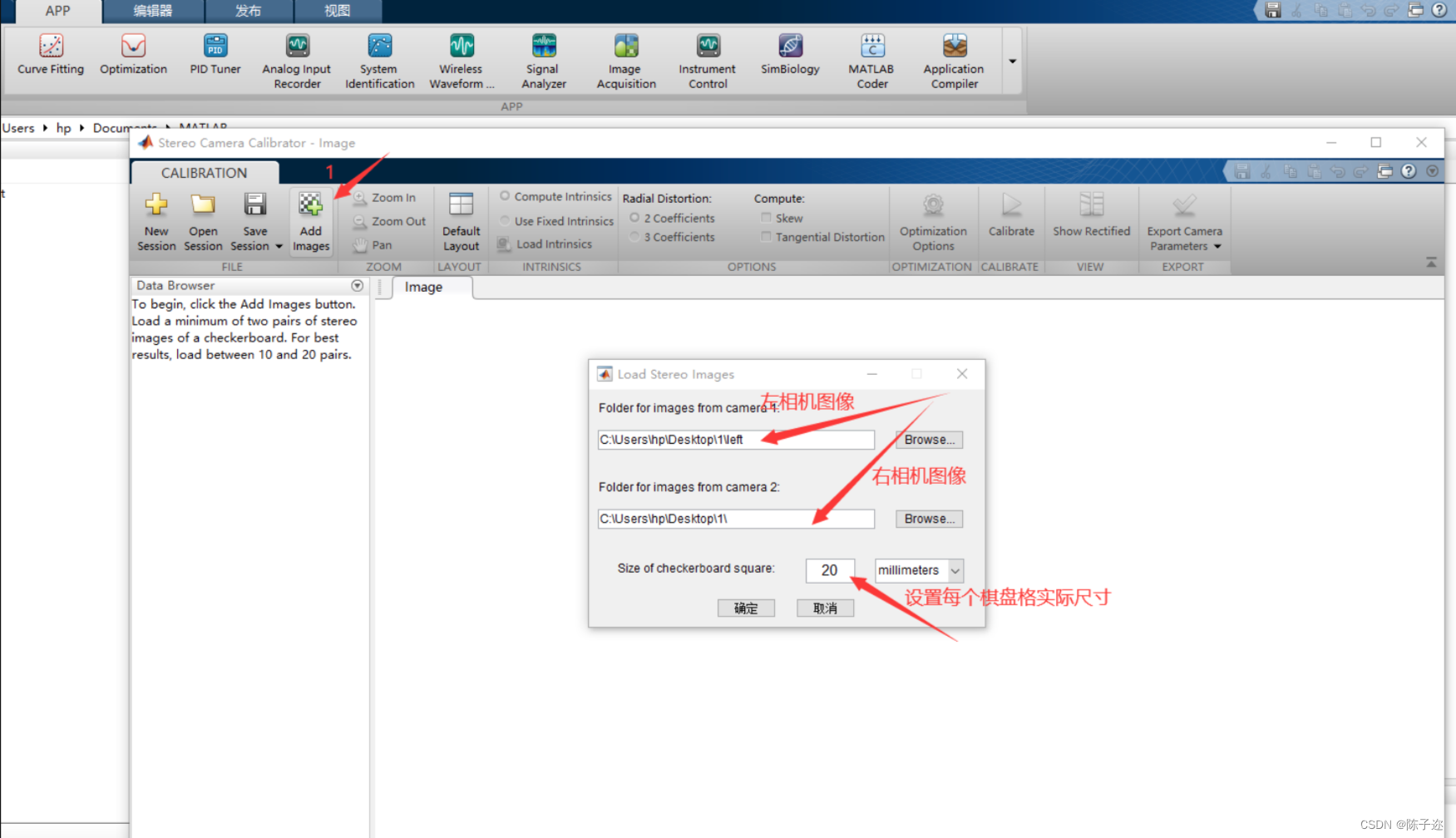
 设置参数，对于一般的相机选择2 Coefficients选项即可，对于大视场相机则选择3 Coefficients选项。拉线删除误差较大的画面：

 2.2 获取参数

在matlab控制台分别输入 stereoParams.CameraParameters1.IntrinsicMatrix 和stereoParams.CameraParameters2.IntrinsicMatrix 获得左右相机的参数，下边填写时请注意进行矩阵的转置

为了获取左相机的畸变系数:[k1, k2, p1, p2, k3]，我们需要分别输入stereoParams.CameraParameters1.RadialDistortion 和 stereoParams.CameraParameters1.TangentialDistortion

分别输入 stereoParams.RotationOfCamera2 和 stereoParams 来获取双目的旋转矩阵和平移矩阵

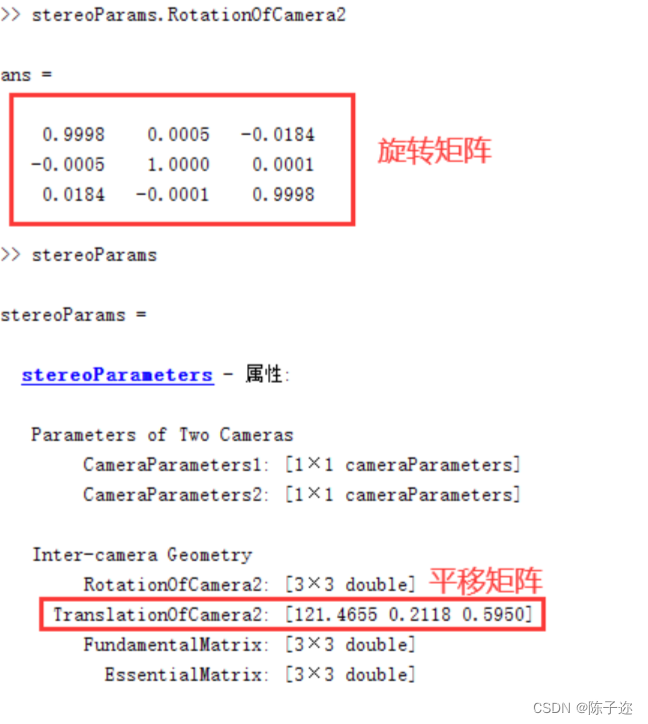
将以上参数填写进stereoconfig.py文件里，注意转置

import numpy as np
 
# 双目相机参数
class stereoCamera(object):
    def __init__(self):
        # 左相机内参
        self.cam_matrix_left = np.array([   [479.6018,   -0.0769,  652.6060],
                                            [       0,  478.0229,  352.3870],
                                            [       0,         0,         1]
                                        ])
        # 右相机内参
        self.cam_matrix_right = np.array([  [489.9354,   0.2789,  641.6219],
                                            [       0,  487.9356,  354.5612],
                                            [       0,         0,         1]
                                        ])
 
        # 左右相机畸变系数:[k1, k2, p1, p2, k3]
        self.distortion_l = np.array([[-0.0791, 0.0309, -0.0009, -0.0004, -0.0091]])
        self.distortion_r = np.array([[-0.1153, 0.1021, -0.0011,  -0.0005,  -0.0459]])
 
        # 旋转矩阵
        self.R = np.array([ [1.0000,  0.0005, -0.0184],
                            [-0.0005,  1.0000, 0.0001],
                            [ 0.0184,  -0.0001,  1.0000]   
                            ])
        # 平移矩阵
        self.T = np.array([[121.4655], [0.2118], [0.5950]])
        # 焦距
        self.focal_length = 749.402 # 默认值，一般取立体校正后的重投影矩阵Q中的 Q[2,3]
        # 基线距离
        self.baseline = 121.4655 # 单位：mm， 为平移向量的第一个参数（取绝对值）

棋盘格图片自提

链接：https://pan.baidu.com/s/1W31fTtr6db8qgTevulWeMA 
提取码：ybca

觉得有帮助的朋友点点赞