数据结构复盘——第二章：线性表

---

第一部分：顺序表

1、顺序表的定义

线性表的顺序存储方式就是用一组地址连续的存储单元依次存储线性表的各个元素，如图所示。可以借助一维数组（+长度）实现。

2、顺序表的操作

顺序表的插入、删除、修改、查找（统称:增删改查）

例如：
插入：AB中间加C 或者 后面加C
修改：把C改为E
删除：把E删除
查找：找到B

3、顺序表的优缺点

• 优点：（对比单链表）
  （1）结构简单；
  （2）可直接定位到表中任一元素，并可随机存取元素；连续存取速度快。
• 缺点：（对比单链表）
  （1）存储空间难于准确静态分配，分配大了浪费空间，分配小了又可能不够用；
  （2）插入、删除操作不大方便，需移动大量数据元素，效率较低。

第一部分习题

1. 在一个长度为 n 的顺序存储的线性表中，向第 i 个元素（1≤i≤n+1）位置插入一个新元素时，需要从后向前依次后移（B）个元素。(代入法)
   A.n-i
   B.n-i+1（以后直接把具体数字代入这个 i ）
   C.n-i-1
   D.i

2. 在一个顺序表的表尾插入一个元素的时间复杂度的量级为(B) 。
   A.O($n$)（头插的最坏情况和其他平均情况下的时间复杂度都是这个）
   B.O($1$)（尾插属于最好情况下的时间复杂度）
   C.O($n\ast n$)
   D.O($lo{g}_{2}n$)

3. 一个向量（即一批地址连续的存储单元）第一个元素的存储地址是100，每个元素的长度为2，则第5个元素的地址是（B) 。
   A.110
   B.108（这个类似于电线杆问题，第 1 个到第 n 个之间有 n-1 个间隔*每个间隔的距离）
   C.100
   D.120

---

第二部分：单链表

1、单链表的定义

在链式存储结构下，线性表的存储空间可以是分散不连续的。
一个指针的存储结点的结构如图所示。

2、单链表的结点知识

（1）结点：通常指和一个数据元素相关的存储空间；
（2）表头元素：线性表中的第一个数据元素；
（3）表尾元素：线性表中的最后一个数据元素；
（4）首元结点：在链式存储结构中，存储线性表中的第一个数据元素；
（5）头结点：在链表的第一个结点（首元结点）之前附设一个结点。
头结点的作用是使用有关链表编程时，空表和非空表可以不分别加以考虑，这样程序既简单又效率高。

• 对于普通的单链表，我们可以依据头结点是否指向空（NULL，即图中^）来判断是不是空表；
• 对于循环链表，表尾结点需要指向头结点，所以可以依据头结点是否指向自身来判断是不是空表。

3、单链表的操作

科普知识：指针是存放内存地址的变量
单链表的插入、删除、修改、查找（统称：增删改查）

• 插入步骤：
  ① q -> next = p ->next；
  ② p -> next = q；
• 头插法和尾插法：
  
• 删除步骤：
  ① p -> next = p -> next -> next；
• 修改和查找步骤：
  ① 一个一个向后查找：p = p->next；
  ② 查找到之后进行修改操作；

4、单链表的优缺点

• 优点：（对比顺序表）
  （1）存储空间动态分配，可以按需要使用。
  （2）插入/删除结点操作时通常只要修改指针，不必移动数据元素。
• 缺点：（对比顺序表）
  （1）每一结点附加指针域。
  （2）非随机存取结构，查找定位操作需从头指针出发顺着链表扫描。

第二部分习题

1. 非空的循环单链表head的尾结点（由p所指向）满足(C) 。
   A.p->next==NULL（普通的单链表尾结点指向空）
   B.p==NULL
   C.p->next==head
   D.p==head

2. 在有n个节点的单链表中，删除指定节点的前趋的时间复杂度是（B）。
   A.O($1$)
   B.O($n$)（链表查找的平均时间复杂度）
   C.O($n^2$)
   D.O($n^3$)

3. 在非空线性链表中由p所指的链节点后面插入一个由 q 所指的链节点的过程是依次执行动作（B）。
   A.q->next=p；p->next=q；
   B.q->next=p->next；p->next=q；
   C.q->next=p->next；p=q；
   D.p->next=g；q->next=p；

---

第三部分：双链表

1、双链表的结构

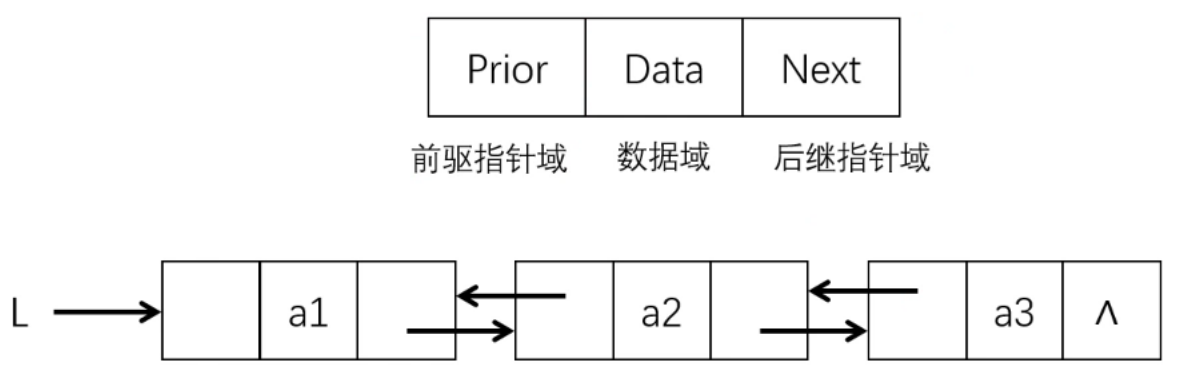
双链表就是但单链表的基础之上给每个结点增加了一个前驱指针域，用于存储上一个结点的内存地址（即指向上一结点）
一个指针的存储结点的结构如图所示。

2、双链表的操作

双链表的插入、删除、修改、查找（统称：增删改查）

• 插入步骤：（p指向插入位置的结点，q指向被插入结点）
  ① q -> next = p -> next ; q -> prior = p；
  ② p -> next -> prior = q；
  ③ p -> next = q；
  
• 删除步骤：（p指向被删除的结点）
  ① p -> next -> prior = p -> prior；p -> prior - > next = p -> next；
  
• 修改和查找步骤：
  ① 和单链表一样，一个一个向后查找：p = p -> next；
  ② 查找到之后进行修改操作；
  ③ 如果是连续的查找操作就可能一个一个向前/向后查找：p = p -> prior；

第三部分习题

1. 在双向循环链表中，在指针 p 指向的结点前插入一个由指针 q 指向的新结点，其修改指针的操作是（C）。【注：双向链表的结点结构为（llink, data，rlink）】
   A.p -> llink = q；q -> rlink = p；p -> llink -> link = q；q -> llink = q；
   B.p -> llink = q；p -> llink -> rlink = q；q -> rlink = p；q -> llink = p -> llink；
   C.q -> rlink = p；q -> llink = p -> llink；p -> llink -> rlink = q；p -> llink = q；
   D.q -> llink = p->llink；q -> rlink = p；p -> llink = q；p -> llink -> rlink = q；

2. 在双向链表存储结构中，删除 p 所指的结点时须修改指针（A）。
   A.p->prior->next=p->next；p->next->prior=p->prior；
   B.p->prior=p->prior->prior；p->prior->next=p；
   C.p->next->prior=p；p->next=p->next->next；
   D.p->next=p->prior->prior；p->prior=p->next->next；

---

第四部分：静态链表

1、静态链表的定义

在无法或者不便于动态生成结点的场合，例如有些高级语言中没有"指针"数据类型，要想发挥链表结构的长处，可用一个一维数组空间（数组元素是结构体，包含数据元素和下一个元素的数组下标）模拟可利用空间表，构造静态链表。

2、静态链表的操作

静态链表的插入、删除、修改、查找（统称：增删改查）

• 插入操作：
  ① 从下标为0的数组元素开始，依照 cursor 的值依次查找，直到访问到被插入位置的前一个元素（例如 a1 ）；
  ② 将待插入元素的 cursor 值设为被插入位置的前一个元素的 cursor 值（例如 a4 的 cursor 设为 a1 的 cursor ）；
  ③ 将被插入位置的前一个元素的 cursor 值设为待插入元素对应的数组下标（例如将 a1 的 cursor 设为3）。

• 删除操作：
  ① 从下标为0的数组元素开始，依照 cursor 的值依次查找，直到访问到待删除元素（例如 a6 ）；
  ② 将待删除元素的前一个元素的 cursor 值设为待删除元素的 cursor 值（例如 a1 的 cursor 设为 a6 的 cursor ）；

• 修改和查找操作：
  ① 从下标为0的数组元素开始，依照 cursor 的值依次访问对应下标的数组元素（例如 a6 ）；
  ② 查找到元素后修改 data 值即可。

第四部分习题

1. 线性表的静态存储结构与顺序存储结构相比，优点是（A）。
   A.所有的操作算法实现简单
   B.便于随机存取（静态链表模拟的是单链表）
   C.便于插入和删除（优点是不需要大量移动元素，但是没法做到随机存取所以不能说便于）
   D.便于利用零散的存储器空间（静态分配一大块区域）

2. 需要分配较大空间，插入和删除不需要移动元素的线性表，其存储结构是（B）。
   A.单链表
   B.静态链表（定义是预先静态分配空间的链表）
   C.线性链表
   D.顺序存储结构

---

小结