-
DL Homework 4
目录
7.激活函数Sigmoid用PyTorch自带函数torch.sigmoid(),观察、总结并陈述。
8.激活函数Sigmoid改变为Relu,观察、总结并陈述。
9.损失函数MSE用PyTorch自带函数 t.nn.MSELoss()替代,观察、总结并陈述。
12.权值w1-w8初始值换为随机数,对比“指定权值”的结果,观察、总结并陈述。
1 整理一下理论收获
1.1 基础理论
前馈神经网络又叫全连接神经网络,多层感知机。
主要的特点为三个
- 层内无连接
- 层外全连接
- 单向传播
因为对于一个训练好的神经网络模型,我们只需要关注这个模型的输入和输出,中间的隐层层的神经元的计算属于黑盒操作,属于一个端到端的学习。
第L层神经元的净输入,我们称净活性值,第L层神经元的输出,我们称为活性值。
我们可以把每个神经层看作一个仿射变换和一个非线性变换。
根据通用相近似定理,对于具有线性输出层和至少一个使用"挤压“性质的激活函数的隐藏层组成的前馈神经网络,只要其隐藏层神经元的数量足够,它可以以任意的精度来近似任何一个定义在实数空间
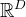 中的有界闭集函数。
中的有界闭集函数。真实的映射函数是未知的,所以一般通过经验分享最小化和正则化来进行参数学习,但是因为神经网络的强大能力,反而更加容易过拟合。(所以引出了我们的正则化项~)
1.2 应用到机器学习
对于二分类问题
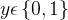 ,并采用Logistic回归,Logistic分类器可以作为神经网络的最后一层(只有一个神经元),并且激活函数为Logistic函数,网络的输出可以作为类别
,并采用Logistic回归,Logistic分类器可以作为神经网络的最后一层(只有一个神经元),并且激活函数为Logistic函数,网络的输出可以作为类别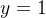 的条件概率
的条件概率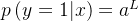
对于多分类问题
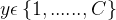 ,如果使用softmax回归分类器,相当于网络最后一层设置C个神经元,其激活函数为softmax函数,网络最后一层(第L层)的输出,可以作为每个类的条件概率,即
,如果使用softmax回归分类器,相当于网络最后一层设置C个神经元,其激活函数为softmax函数,网络最后一层(第L层)的输出,可以作为每个类的条件概率,即
多分类回归的输出要经过归一化处理才可以作为条件概率,因为它们的和可能不为1。为了使这些输出值可以解释为概率,我们需要对它们进行归一化处理。
1.3 参数学习
给定训练集
 ,将每个样本
,将每个样本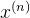 输入给前馈神经网络,得到网络输出为
输入给前馈神经网络,得到网络输出为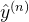 ,其在数据集
,其在数据集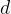 上的结构化风险为
上的结构化风险为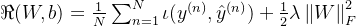
其中
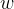 和
和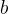 分别表示网络中的所有的权重矩阵和偏置向量;
分别表示网络中的所有的权重矩阵和偏置向量;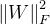 是正则化项,用来防止过拟合;
是正则化项,用来防止过拟合;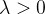 为超参数,
为超参数,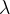 越大,
越大,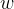 越接近于0,这里的
越接近于0,这里的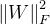 一般使用
一般使用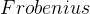 范数(
范数(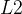 范数):
范数):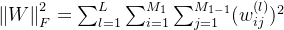
首先简单解释一下这堆话,结构化风险=经验风险+正则化项,经验风险为
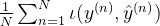 ,对于
,对于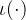 函数我们大多数采取的为交叉熵函数,
函数我们大多数采取的为交叉熵函数,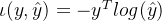 ,正则化项为
,正则化项为 ,上述其实有堆正则化项的描述但不具体,这里根据鱼书详细介绍一下正则化,首先神经网络的学习目的是减小损失函数的值,并且防止训练集的过拟合,这时,例如为损失函数加上
,上述其实有堆正则化项的描述但不具体,这里根据鱼书详细介绍一下正则化,首先神经网络的学习目的是减小损失函数的值,并且防止训练集的过拟合,这时,例如为损失函数加上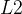 范数,也就是我们所说的正则化项。这样一来,就可以抑制权重变大。 用符号表示的话,如果将权重记为
范数,也就是我们所说的正则化项。这样一来,就可以抑制权重变大。 用符号表示的话,如果将权重记为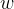 ,
,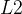 范数的权值衰减就是
范数的权值衰减就是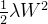 ,然 后将这个
,然 后将这个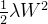 加到损失函数上。这里,
加到损失函数上。这里,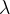 是控制正则化强度的超参数。
是控制正则化强度的超参数。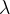 设置得越大,对大的权重施加的惩罚就越重。此外,
设置得越大,对大的权重施加的惩罚就越重。此外,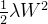 开头的
开头的 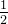 是用于将
是用于将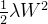 的求导结果变成
的求导结果变成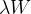 的调整用常量。
的调整用常量。对于所有权重,权值衰减方法都会为损失函数加上
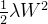 。因此,在求权重梯度的计算中,要为之前的误差反向传播法的结果加上正则化项的导数
。因此,在求权重梯度的计算中,要为之前的误差反向传播法的结果加上正则化项的导数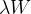 。
。正则化项可以为
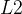 范数,但不知有
范数,但不知有 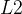 范数,还有
范数,还有  范数、
范数、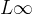 范数等。
范数等。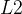 范数相当于各个元素的平方和。用数学式表示的话,假设有权重 \(W = (w_1, w_2, ... , w_n)\),则
范数相当于各个元素的平方和。用数学式表示的话,假设有权重 \(W = (w_1, w_2, ... , w_n)\),则 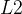 范数可用 \(\sqrt{w_1^2+w_2^2+...+w_n^2}\)计算出来。
范数可用 \(\sqrt{w_1^2+w_2^2+...+w_n^2}\)计算出来。 范数是各个元素的绝对值之和,相当于\(|w_1| + |w_2| + ... + |w_n|\)。
范数是各个元素的绝对值之和,相当于\(|w_1| + |w_2| + ... + |w_n|\)。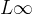 范数也称为 \(Max\)范数,相当于各个元素的绝对值中最大的那一个。
范数也称为 \(Max\)范数,相当于各个元素的绝对值中最大的那一个。
1.4 反向传播算法
不是讲什么是反向传播算法哦!知识对我这一快我学到的一些东西进行汇总。
反向传播算法的流程很像贡献度分配问题,通过链式法则逐一对参数求偏导比较低效,所以采取反向传播算法。
1.为什么要利用梯度方向进行更新
因为梯度方向更新是最快的,为了提升时间效率,所以采取梯度方向更新
2.神经网络的激活函数必须使用非线性函数。换句话说,激活函数不能使 用线性函数。为什么不能使用线性函数呢?
因为使用线性函数的话,加深神经网络的层数就没有意义.线性函数的问题在于,不管如何加深层数,总是存在与之等效的“无 隐藏层的神经网络”,利用鱼书里的例子来解释,这里我们把\(h(x) = cx\)作为激活函数,把\(y=h(h(h(x)))\)的运算对应3层神经网络。这个运算会进行\(y(x) = c*c*c*x\)的乘法运算,但同样处理可以有\(y(x)=ax(a=c^3)\)这一次乘法运算(即没有隐藏层的神经网络)来表示,如本例所示, 使用线性函数时,无法发挥多层网络带来的优势。因此,为了发挥隐藏层所带来的优势,激活函数必须使用非线性函数。
3.什么是链式法则
关于链式法则,在鱼书中是这样定义的
链式法则是关于复合函数的导数的性质,如果某个函数由复合函数表示,则该复合函数的导数可以用构成复合函数的各个函数的导数的乘积表示
同样是用鱼书中的例子来简单说明一下:
\(z=(x+y)^2\)可以看成一个复合函数,是由\(z=t^2\)和\(t=x+y\)构成的,\(\frac{\partial_{z}}{\partial _x}\)可以用\(\frac{\partial_{z}}{\partial _t}\)和\(\frac{\partial_{t}}{\partial _x}\)表示
\(\frac{\partial_{z}}{\partial _x}=\frac{\partial_{z}}{\partial _t}*\frac{\partial_{t}}{\partial _x}\) 而式子中的\(\partial_t\)正好可以相互抵消,这就是链式法则,并且在鱼书中已明确指出,反向传播是基于链式法则的。
2.激活函数
首先介绍一下本文使用的激活函数(虽然之前提过一次了,但是为了下次不犯错,多提几次没啥事)
\(sigmoid(x) = \frac{1}{1+e^{-x}}\)
这里给出一个结论:\({sigmoid(x)}' = sigmoid(x) * (1 - sigmoid(x))\)
证明:\({sigmoid(x)}'=e^{-x}* (1+e^{-x})^{-2}\)
\(sigmoid(x)*(1 - sigmoid(x)) = \frac{1}{1 + e^{-x}} * \frac{e^{-x}}{1+e^{-x}}=e^{-x} * (1 + e^{-x}) ^ {-2}\)
证明成功,bingo!!!!!
激活函数可以是\(sigmoid\)函数、也可以是\(Relu\)函数,不局限这两个,但是这两个最常用,本篇也是围绕二者进行讨论。
铺垫到此为止,下面开始本文的正文!!!
3.神经网络流程推导(包含正向传播和反向传播)
上图,对这样一个神经网络进行推导,以下欢迎来到眼花缭乱篇~

参数表 \(x_1,x_2\) 模型的输入 \(w_1,w_2,..,w_8\) 神经元层之间连接的权重 \(h_1,h_2\) 隐藏层的活性值 \(In_{h_1},In_{h_2}\) 隐藏层的净活性值 \(o_1,o_2\) 输出层的活性值 \(In_{o_1},In_{o_2}\) 输出层的净活性值 \(Error\) 输出层的活性值与真实标签的均方误差 \(sigmoid\) 激活函数 首先,正向传播过程如下:
\(In_{h_1} = x_1*w_1+x_2*w_3\) \(h_1 = sigmoid(In_{h_1})\)
\(In_{h_2}=x_1*w_2+x_2*w_4\) \(h_2=sigmoid(In_{h_2})\)
\(In_{o_1} = h_1*w_5+h_2*w_7\) \(o_1=sigmoid(In_{o_1})\)
\(In_{o_2}=h_1*w_6+h_2*w_8\) \(o_2=sigmoid(In_{o_2})\)
\(Error = \frac{(o_1-y_1)^2}{2} + \frac{(o_2-y_2)^2}{2}\)
利用链式法则,求解神经元层的误差项:
\(\delta_{w_5} = \frac{\partial _{Error}}{\partial _{w_5}}=\frac{\partial_{Error}}{\partial _{o_1}}*\frac{\partial _{o_1}}{\partial _{In_{o_1}}}*\frac{\partial _{In_{o_1}}}{\partial _{w_5}}\)
\(\delta_{w_6} = \frac{\partial _{Error}}{\partial _{w_6}}=\frac{\partial_{Error}}{\partial _{o_2}}*\frac{\partial _{o_2}}{\partial_{In_{o2}}}*\frac{\partial_{In_{o2}}}{\partial _{w_6}}\)
\(\delta_{w_7} = \frac{\partial _{Error}}{\partial _{w_7}}=\frac{\partial_{Error}}{\partial _{o_1}}*\frac{\partial _{o_1}}{\partial _{In_{o_1}}}*\frac{\partial _{In_{o_1}}}{\partial _{w_7}}\)
\(\delta_{w_8} = \frac{\partial _{Error}}{\partial _{w_8}}=\frac{\partial_{Error}}{\partial _{o_2}}*\frac{\partial _{o_2}}{\partial_{In_{o2}}}*\frac{\partial_{In_{o2}}}{\partial _{w_8}}\)
\(\delta_{w_1} = \frac{\partial _{Error}}{\partial _{w_1}}=(\frac{\partial_{Error}}{\partial _{o_1}}*\frac{\partial _{o_1}}{\partial _{In_{o_1}}}*\frac{\partial _{In_{o_1}}}{\partial _{h_1}}+\frac{\partial _{Error}}{\partial _{o_2}}*\frac{\partial_{o_2}}{\partial_{In_{o_2}}}*\frac{\partial _{In_{o_2}}}{\partial _{h_1}})*\frac{\partial_{h_1}}{\partial_{In_{h_1}}}*\frac{\partial _{In_{h_1}}}{w_1}\)
\(\delta_{w_2} = \frac{\partial _{Error}}{\partial _{w_2}}=(\frac{\partial_{Error}}{\partial _{o_1}}*\frac{\partial _{o_1}}{\partial _{In_{o_1}}}*\frac{\partial _{In_{o_1}}}{\partial _{h_2}}+\frac{\partial _{Error}}{\partial _{o_2}}*\frac{\partial_{o_2}}{\partial_{In_{o_2}}}*\frac{\partial _{In_{o_2}}}{\partial _{h_2}})*\frac{\partial_{h_2}}{\partial_{In_{h_2}}}*\frac{\partial _{In_{h_2}}} {w_2}\)
\(\delta_{w_3} = \frac{\partial _{Error}}{\partial _{w_3}}=(\frac{\partial_{Error}}{\partial _{o_1}}*\frac{\partial _{o_1}}{\partial _{In_{o_1}}}*\frac{\partial _{In_{o_1}}}{\partial _{h_1}}+\frac{\partial _{Error}}{\partial _{o_2}}*\frac{\partial_{o_2}}{\partial_{In_{o_2}}}*\frac{\partial _{In_{o_2}}}{\partial _{h_1}})*\frac{\partial_{h_1}}{\partial_{In_{h_1}}}*\frac{\partial _{In_{h_1}}}{w_3}\)
\(\delta_{w_4} = \frac{\partial _{Error}}{\partial _{w_4}}=(\frac{\partial_{Error}}{\partial _{o_1}}*\frac{\partial _{o_1}}{\partial _{In_{o_1}}}*\frac{\partial _{In_{o_1}}}{\partial _{h_2}}+\frac{\partial _{Error}}{\partial _{o_2}}*\frac{\partial_{o_2}}{\partial_{In_{o_2}}}*\frac{\partial _{In_{o_2}}}{\partial _{h_2}})*\frac{\partial_{h_2}}{\partial_{In_{h_2}}}*\frac{\partial _{In_{h_2}}}{w_4}\)
根据误差项对参数进行修正:
\(w_1 = w_1 + l * \delta _{w_1}\)
\(w_2 = w_2 + l * \delta _{w_2}\)
\(w_3 = w_3 + l * \delta _{w_3}\)
\(w_4 = w_4 + l * \delta _{w_4}\)
\(w_5 = w_5 + l * \delta _{w_5}\)
\(w_6 = w_6 + l * \delta _{w_6}\)
\(w_7 = w_7 + l * \delta _{w_7}\)
\(w_8 = w_8 + l * \delta _{w_8}\)
4.数值计算 - 手动计算
时间原因,之后会补上滴
5.代码实现 - numpy手推
- import numpy as np
- w1, w2, w3, w4, w5, w6, w7, w8 = 0.2, -0.4, 0.5, 0.6, 0.1, -0.5, -0.3, 0.8 # 初始权值
- x1, x2 = 0.5, 0.3 # 输入x
- y1, y2 = 0.23, -0.07 # 真实标签 y
- print("模型的输入为",x1, x2)
- # sigmoid函数
- def sigmoid(x):
- return 1 / (1 + np.exp(-x))
- # 向前传播
- def forward(x1, x2, w1, w2, w3, w4, w5, w6, w7, w8):
- h1_in = x1 * w1 + x2 * w3
- h2_in = x1 * w2 + x2 * w4
- h1_out = sigmoid(h1_in)
- h2_out = sigmoid(h2_in)
- print("隐藏层输出为", round(h1_out, 4), round(h2_out, 4))
- o1_in = h1_out * w5 + h2_out * w7
- o2_in = h1_out * w6 + h2_out * w8
- o1_out = sigmoid(o1_in)
- o2_out = sigmoid(o2_in)
- print("模型输出为", round(o1_out, 4), round(o2_out, 4))
- return h1_out, h2_out, o1_out, o2_out
- def backword(h1, h2, o1, o2, y1, y2, x1, x2, w5, w6, w7, w8):
- d_w5 = (o1 - y1) * o1 * (1 - o1) * h1
- d_w6 = (o2 - y2) * o2 * (1 - o2) * h1
- d_w7 = (o1 - y1) * o1 * (1 - o1) * h2
- d_w8 = (o2 - y2) * o2 * (1 - o2) * h2
- d_w1 = ((o1 - y1) * o1 * (1 - o1) * w5 + (o2 - y2) * o2 * (1 - o2) * w6) * h1 * (1 - h1) * x1
- d_w2 = ((o1 - y1) * o1 * (1 - o1) * w7 + (o2 - y2) * o2 * (1 - o2) * w8) * h2 * (1 - h2) * x1
- d_w3 = ((o1 - y1) * o1 * (1 - o1) * w5 + (o2 - y2) * o2 * (1 - o2) * w6) * h1 * (1 - h1) * x2
- d_w4 = ((o1 - y1) * o1 * (1 - o1) * w7 + (o2 - y2) * o2 * (1 - o2) * w8) * h2 * (1 - h2) * x2
- print("w的梯度:", round(d_w1, 2), round(d_w2, 2), round(d_w3, 2), round(d_w4, 2), round(d_w5, 2), round(d_w6, 2),
- round(d_w7, 2), round(d_w8, 2))
- return d_w1, d_w2, d_w3, d_w4, d_w5, d_w6, d_w7, d_w8
- def updata(d_w1, d_w2, d_w3, d_w4, d_w5, d_w6, d_w7, d_w8, w1, w2, w3, w4, w5, w6, w7, w8, l):
- w1 = w1 - d_w1 * l
- w2 = w2 - d_w2 * l
- w3 = w3 - d_w3 * l
- w4 = w4 - d_w4 * l
- w5 = w5 - d_w5 * l
- w6 = w6 - d_w6 * l
- w7 = w7 - d_w7 * l
- w8 = w8 - d_w8 * l
- return w1, w2, w3, w4, w5, w6, w7, w8
- def error(o1, o2, y1, y2):
- return ((o1 - y1) ** 2 + (o2 - y2) ** 2) / 2
- count = 50
- for k in range(count):
- print("\n=====第" + str(k + 1) + "轮=====")
- h1_out, h2_out, o1_out, o2_out = forward(x1, x2, w1, w2, w3, w4, w5, w6, w7, w8)
- print("模型的损失函数(均方误差):",round(error(o1_out, o2_out, y1, y2), 4))
- d_w1, d_w2, d_w3, d_w4, d_w5, d_w6, d_w7, d_w8 = backword(h1_out, h2_out, o1_out, o2_out, y1, y2, x1, x2, w5, w6, w7, w8)
- w1, w2, w3, w4, w5, w6, w7, w8 = updata(d_w1, d_w2, d_w3, d_w4, d_w5, d_w6, d_w7, d_w8, w1, w2, w3, w4, w5, w6, w7, w8, 1)
- print("更新后的权值w:", round(w1, 4), round(w2, 4), round(w3, 4), round(w4, 4), round(w5, 4), round(w6, 4),round(w7, 4),round(w8, 4))
6.代码实现 - pytorch自动
- import torch
- import datetime
- x = [0.5, 0.3]
- y = [0.23, -0.07]
- print("输入为",x)
- w = [torch.Tensor([0.2]), torch.Tensor([-0.4]), torch.Tensor([0.5]), torch.Tensor(
- [0.6]), torch.Tensor([0.1]), torch.Tensor([-0.5]), torch.Tensor([-0.3]), torch.Tensor([0.8])]
- for i in range(0, 8):
- w[i].requires_grad = True
- def sigmoid(x):
- return 1 / (1 + torch.exp(-x))
- def forward(x):
- h1_in = w[0] * x[0] + w[2] * x[1]
- h2_in = w[1] * x[0] + w[3] * x[1]
- h1_out = sigmoid(h1_in)
- h2_out = sigmoid(h2_in)
- print("隐藏层输出为", h1_out.data, h2_out.data)
- o1_in = w[4] * h1_out + w[6] * h2_out
- o2_in = w[5] * h1_out + w[7] * h2_out
- o1_out = sigmoid(o1_in)
- o2_out = sigmoid(o2_in)
- print("模型输出为", o1_out.data, o2_out.data)
- return o1_out, o2_out
- def error(pre, y):
- loss = (1 / 2) * (pre[0] - y[0]) ** 2 + (1 / 2) * (pre[1] - y[1]) ** 2
- return loss
- start=datetime.datetime.now()
- count = 50
- for k in range(count):
- print("\n=====第" + str(k + 1) + "轮=====")
- pre = forward(x)
- loss = error(pre, y)
- print("模型的损失函数(均方误差):", loss.data)
- loss.backward()
- l = 1 #学习率
- print("w的梯度", end=" ")
- for i in range(0, 8):
- print(round(w[i].grad.item(), 2), end=" ")
- w[i].data = w[i].data - l * w[i].grad.data
- w[i].grad.data.zero_()
- print("\n更新后的权值w:", end="")
- for i in range(0, 8):
- if i == 3:
- print()
- print(w[i].data, end=" ")
- end=datetime.datetime.now()
- print('Running time: %s Seconds'%(end-start))
总结:两个代码就代码量来讲pytorch把BP算法的过程给封装起来了,肯定是比numpy手推要好,代码的效果展示如下:
numpy:

pytorch:

我们发现同时对模型运行50次,numpy和pytorch运行的效果都是一样的
并且通过阅读大佬的博客,我发现,最终这个模型会完全收敛,展示如下:
numpy:

pytorch:

在更改模型运行次数的时候,我突然有了一个想法,封装好的BP运行快还是我们自己手写的快,于是我引入了时间函数进行比较,模板如下,有兴趣的自行添加:
- #该方法包含了其他程序使用CPU的时间,所以跑两个代码的时候最好不要动别的
- import datetime
- start=datetime.datetime.now()
- #中间写代码块
- end=datetime.datetime.now()
- print('Running time: %s Seconds'%(end-start))
pytorch:

numpy:

我们发现才1000次,差距就出来了,那遇到大型数据的是差距肯定更明显,但是为什么呢,怀揣着疑问,我去搜索了资料,好像也没搜出来个所以然,我觉得可能就是tensor张量和列表的操作影响的吧虽然操作相同但是不同的对象,张量就浪费更多的时间,还有待求证,但是问题不大
7.激活函数Sigmoid用PyTorch自带函数torch.sigmoid(),观察、总结并陈述。
- # 只需要更改一个forward函数足以
- def forward(x):
- h1_in = w[0] * x[0] + w[2] * x[1]
- h2_in = w[1] * x[0] + w[3] * x[1]
- h1_out = torch.sigmoid(h1_in)
- h2_out = torch.sigmoid(h2_in)
- print("隐藏层输出为", h1_out.data, h2_out.data)
- o1_in = w[4] * h1_out + w[6] * h2_out
- o2_in = w[5] * h1_out + w[7] * h2_out
- o1_out = torch.sigmoid(o1_in)
- o2_out = torch.sigmoid(o2_in)
- print("模型输出为", o1_out.data, o2_out.data)
- return o1_out, o2_out
结果展示如下:


这而让我很蒙圈,我看大佬的博客都说有微小区别,但是我这儿相似的一批,可能是小数点后好几位可能有不同,但是犹豫对模型影响过小,可以忽略不计,这里就不多家阐述咯,下面附件一个看到的很好的批注,偷过来,咳咳(手动花花,给刘学长)
torch.sigmoid()、torch.nn.Sigmoid()和torch.nn.functional.sigmoid()有区别, 比如:
torch.sigmoid():这是一个方法,包含了参数和返回值。torch.nn.Sigmoid():这是一个类。在定义模型的初始化方法中使用,需要在_init__中定义,然后在使用。
torch.nn.functional.sigmoid():这是一个方法,可以直接在正向传播中使用,而不需要初始化;在训练模型的过程中,也可以直接使用。
8.激活函数Sigmoid改变为Relu,观察、总结并陈述。
- # 修改一个forward函数足以
- def forward(x):
- h1_in = w[0] * x[0] + w[2] * x[1]
- h2_in = w[1] * x[0] + w[3] * x[1]
- h1_out = torch.relu(h1_in)
- h2_out = torch.relu(h2_in)
- print("隐藏层输出为", h1_out.data, h2_out.data)
- o1_in = w[4] * h1_out + w[6] * h2_out
- o2_in = w[5] * h1_out + w[7] * h2_out
- o1_out = torch.relu(o1_in)
- o2_out = torch.relu(o2_in)
- print("模型输出为", o1_out.data, o2_out.data)
- return o1_out, o2_out
结果展示如下:


我们发现结果很明显,在50轮的时候就可以发现,使用Relu激活函数模型损失函数也就是均方误差下降的比用sigmoid激活函数模型快,使用Relu激活函数模型收敛速度是要优于使用sigmoid激活函数模型,那究竟是为什么呢?
- Relu函数的收敛速度比sigmoid函数更快。这是由于Relu函数将所有的负值都变为0,而正值不变,这种操作被称为单侧抑制。
- sigmoid函数在深度网络训练中可能会出现梯度消失的问题。由于sigmoid函数是软饱和的,当输入值非常大或非常小的时候,其导数会趋于0,这就会导致梯度下降优化算法更新网络的速度变慢,从而影响模型的训练和收敛速度。相反,Relu函数没有这个问题,它的梯度在大多数时候都是非零的,因此使用梯度下降优化算法更新网络的速度更快。
9.损失函数MSE用PyTorch自带函数 t.nn.MSELoss()替代,观察、总结并陈述。
- import torch
- x = [0.5, 0.3]
- y = [torch.Tensor([0.23]), torch.Tensor([-0.07])]
- print("输入为",x)
- w = [torch.Tensor([0.2]), torch.Tensor([-0.4]), torch.Tensor([0.5]), torch.Tensor(
- [0.6]), torch.Tensor([0.1]), torch.Tensor([-0.5]), torch.Tensor([-0.3]), torch.Tensor([0.8])]
- # w = [torch.randn(1,1), torch.randn(1,1), torch.randn(1,1), torch.randn(1,1), torch.randn(1,1), torch.randn(1,1), torch.randn(1,1), torch.randn(1,1)]
- # w = [torch.Tensor([0]), torch.Tensor([0]), torch.Tensor([0]), torch.Tensor([0]), torch.Tensor([0]), torch.Tensor([0]), torch.Tensor([0]), torch.Tensor([0])]
- for i in range(0, 8):
- w[i].requires_grad = True
- def forward(x):
- h1_in = w[0] * x[0] + w[2] * x[1]
- h2_in = w[1] * x[0] + w[3] * x[1]
- h1_out = torch.sigmoid(h1_in)
- h2_out = torch.sigmoid(h2_in)
- print("隐藏层输出为", h1_out.data, h2_out.data)
- o1_in = w[4] * h1_out + w[6] * h2_out
- o2_in = w[5] * h1_out + w[7] * h2_out
- o1_out = torch.sigmoid(o1_in)
- o2_out = torch.sigmoid(o2_in)
- print("模型输出为", o1_out.data, o2_out.data)
- o1_out = torch.Tensor(o1_out)
- o2_out = torch.Tensor(o2_out)
- return o1_out, o2_out
- def error(pre, y):
- mes_loss = torch.nn.MSELoss()
- loss = mes_loss(pre[0], y[0]) + mes_loss(pre[1], y[1])
- return loss
- count = 1000
- for k in range(count):
- print("\n=====第" + str(k + 1) + "轮=====")
- pre = forward(x)
- loss = error(pre, y)
- print("模型的损失函数(均方误差):", loss.data)
- loss.backward()
- l = 1 #学习率
- print("w的梯度", end=" ")
- for i in range(0, 8):
- print(round(w[i].grad.item(), 2), end=" ")
- w[i].data = w[i].data - l * w[i].grad.data
- w[i].grad.data.zero_()
- print("\n更新后的权值w:", end="")
- for i in range(0, 8):
- if i == 3:
- print()
- print(w[i].data, end=" ")
展示一下运行的结果:


从结果来看,torch.nn.MSELoss的反馈不如手写的,收敛的效果不好
灵感来了挡不住啊,首先解决一下大佬博客中提到的那个问题
 只要把torch.tensor函数改为torch.Tensor类方法就好了,具体的巴拉巴拉上网搜好多解释,我也没咋看懂,全是英文,那个文档,但是会解决这个问题了,我真是太强了,等有时间还得详细再研究一下,嘿嘿嘿。
只要把torch.tensor函数改为torch.Tensor类方法就好了,具体的巴拉巴拉上网搜好多解释,我也没咋看懂,全是英文,那个文档,但是会解决这个问题了,我真是太强了,等有时间还得详细再研究一下,嘿嘿嘿。
10.损失函数MSE改变为交叉熵,观察、总结并陈述。
- # 只需要修改error一部分的代码即可
- def error(pre, y):
- loss_func = torch.nn.CrossEntropyLoss()
- # loss = mes_loss(pre[0], y[0]) + mes_loss(pre[1], y[1])
- y_pred = torch.stack([pre[0], pre[1]], dim=1)
- y = torch.stack([y[0], y[1]], dim=1)
- loss = loss_func(y_pred, y) # 计算
- return loss
运行结果如下:


到交叉熵损失在训练1000轮后是个负数,有个负对数,当网络输出的概率是0-1时,正数。可当网络输出大于1的数,就有可能变成负数。所以输出的时候可以调用者softmax函数。
11.改变步长,训练次数,观察、总结并陈述。
训练次数一直都是以两个训练次数为例,这里不多加赘述了,改变步长计算
将步长为1的模型训练过程的损失函数进行可视化,结果如下:

我们发现步长为1的时候收敛的速度很快
我们初始的步长为1,现在缩小步长令步长(我更喜欢叫学习率)为0.1,结果如下:


由结果发现,学习率降低的时候,影响的是模型收敛的速度,哪怕执行了1000次,模型还没有完全收敛,经过测试大概当步长为0.1时大概需要1300次才能使模型收敛:

损失函数和训练轮次的关系如下:

缩小步长就会减小收敛速度,那么增加步长会不会就增加收敛速度了呢
epoch = 50, l = 5


确实快了好多!!!接着让我们继续放大步长看一看
epoch = 1000, l = 50

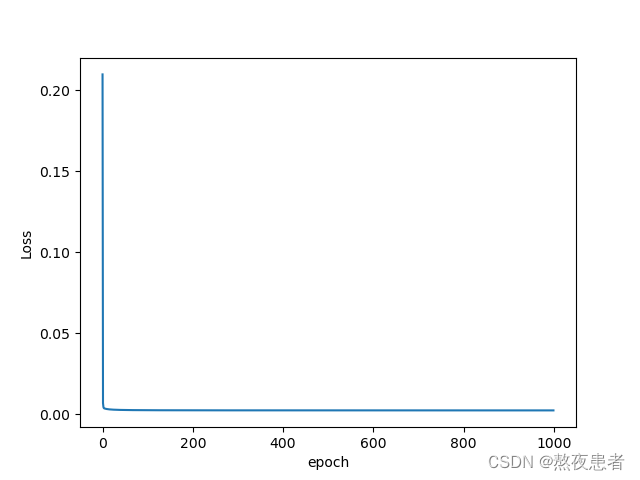
这里为了更加细致的观看收敛的情况,我也展示了50次训练的关系图

讲实话,我最开始以为这个情况就是模型崩了,后来才知道这个情况只是模型收敛的太快
epoch = 50, l = 500
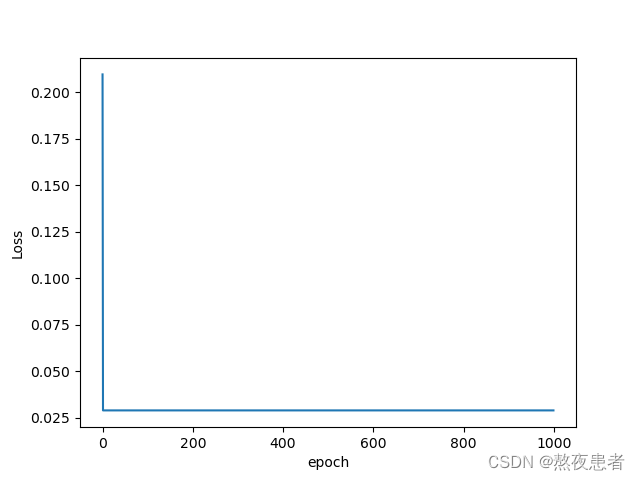

均方误差远大于原来的均方误差,这才叫崩了,长见识了
很明显,我们可以发现step调小一个级数,会使收敛速度减慢, step调大一个级数,会使收敛速度加快,但是一定要在模型能接受的范围内,不然就会适得其反咯.
(PS:看行哥的实验代码,他epoch=1000, l=50说是和epoch=1000,l=1收敛结果一样,但是我坚持查了好几遍反复确认我的代码没有问题,所以我感觉他有问题!对没错,我是不会错的,于是我去搜索了一下,我才知道收敛结果指的是均方误差,而不是最后拟合的w,我都差点准备给他发消息了,结果发现自己错了,家人们谁懂啊)
12.权值w1-w8初始值换为随机数,对比“指定权值”的结果,观察、总结并陈述。
w = [torch.randn(1,1)] * 8

可以看出,权重的初始化不会影响收敛的结果,只会影响收敛的速度
13.权值w1-w8初始值换为0,观察、总结并陈述。
w = [torch.Tensor([0]), torch.Tensor([0]), torch.Tensor([0]), torch.Tensor([0]), torch.Tensor([0]), torch.Tensor([0]), torch.Tensor([0]), torch.Tensor([0])]

结论只会改变收敛的速度,不会改变最终的结果
PS:又要长脑子了,首先我使用的代码为 w = [torch.Tensor([0])] * 8,运行的结果如下 :


然后,我就傻了,我看着行哥的结论,不影响收敛结果,理论上说也不影响收敛结果,那为什么么,我cpu都烧了,后来百度了一下才知道
w = [torch.Tensor([0])] * 8:这个语句会创建一个长度为8的列表,列表中的每个元素都是同一个torch.Tensor([0])的引用。这意味着,如果你更改了列表中的任何一个Tensor对象(比如改变了它的值),那么所有的Tensor对象都会被更改,因为它们都是指向同一个对象的引用。w = [torch.Tensor([0]), torch.Tensor([0]), torch.Tensor([0]), torch.Tensor([0]), torch.Tensor([0]), torch.Tensor([0]), torch.Tensor([0]), torch.Tensor([0])]:这个语句会创建一个长度为8的列表,列表中的每个元素都是独立的Tensor对象。每个Tensor对象都存储了自己的值,更改其中一个Tensor对象不会影响到其他的Tensor对象。
简而言之,第一种方式创建的是一个包含8个对同一个
Tensor对象的引用的列表,而第二种方式创建的是一个包含8个独立的Tensor对象的列表。哇塞,又长脑子了耶。
14.全面总结反向传播原理和编码实现,认真写心得体会。
1.关于为什么按照梯度更新,激活函数为什么是非线性的等等的基础理论一定要明确
2.对BP推到的这个手动的过程一定要明确,而非只会一个backward即可,不利于学习
3.不同激活函数表现出来得性能是不一样的,要明确,像使用Relu激活函数收敛速度就要优于sigmoid激活函数
4.适当的改变学习率可以对模型进行优化,使模型收敛的更快,训练次数也要调整,不然浪费资源
5.对权值的初始化的更改,我们明确了,权值不影响最后的收敛结果,只不过会影响收敛的速度而已
6.交叉熵损失函数结果是有可能出现负数的情况的,需要结合softmax函数一起用。
历时快20个小时的博客,写完咯,有点自豪,从一点点编辑公式,到一点点修正error,脑子好痒,好像要长脑子咯,也很庆幸自己没放弃,芜湖~总之这篇博客写完,让我对深度学习的学习有了一定的自信,不像最开始那样束手束脚了,而且认认真真的写完一篇博客真的让人收益良多,虽然很累,但是很充实,很满足,下次继续!有问题的也欢迎积极指正!
代码会写,但是忘了可视化了,看了大佬的代码才想起来,咳咳,感谢多位大佬的博客
pytorch中backward()函数详解_backward函数-CSDN博客NNDL 作业3:分别使用numpy和pytorch实现FNN例题_。没有用n,nly,kkn3_笼子里的薛定谔的博客-CSDN博客 【人工智能导论:模型与算法】MOOC 8.3 误差后向传播(BP) 例题 【第三版】 - HBU_DAVID - 博客园 (cnblogs.com)
-
相关阅读:
java io流
【C++项目】手动实现一个定长内存池(了解内存分配机制、定长内存提高效率 附源码)
【译】如何使库与本机 AOT 兼容(二)
卡尔曼滤波器的通俗理解
为什么C语言需要指定平台开发?
ubuntu安装 miniconda 同步时间
2.3 Go语言中的字符型和常量定义
Docker安装Redis
结构体类型数据单链表的操作
Rflysim | 传感器标定与测量实验二
- 原文地址:https://blog.csdn.net/m0_70026215/article/details/133799177
