-
强化学习(Reinforcement Learning)与策略梯度(Policy Gradient)
写在前面:本篇博文的内容来自李宏毅机器学习课程与自己的理解,同时还参考了一些其他博客(
懒得放链接)。博文的内容主要用于自己学习与记录。1 强化学习的基本框架
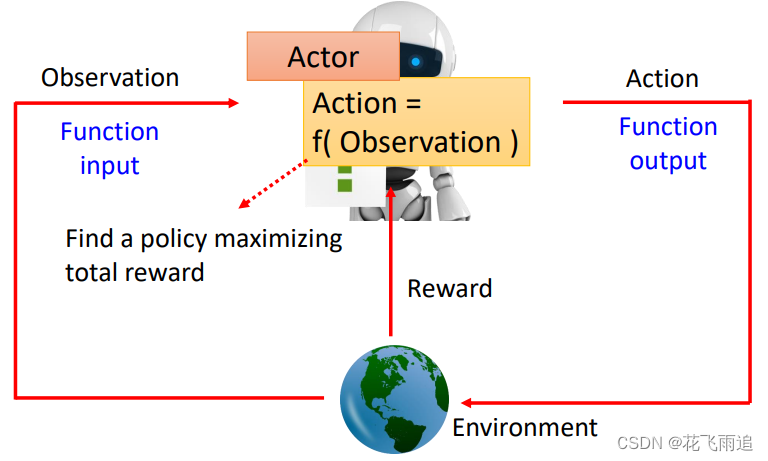
强化学习(Reinforcement Learning, RL)主要由智能体(Agent/Actor)、环境(Environment)、状态(State)、动作(Action)、奖励(Reward)组成。在这些成员中,需要训练的是智能体,他会根据不同的状态产生动作。具体过程见下图,智能体由环境得到Observation(状态),再根据Observation得到一个动作作用于环境产生一个新的环境,再根据之前的状态和动作会给出奖励(正奖励或者负奖励)。随后,智能体根据新的状态和奖励,按照一定的策略执行新的动作。智能体通过强化学习,可以知道自己在什么状态下,应该采取什么样的动作使得自身获得最大奖励。
2 强化学习基本步骤
2.1 步骤1:构建决策框架
对于智能体(后文都用Actor)模块,很容易想到构建一个用于分类任务的Neural Network,根据例如图像一类的输入,通过Neural Network的计算得到每个动作的概率,选最大概率的动作作为最终的动作。再根据最终的Reward进行反向传播更新权重,从而达到训练的效果。这是典型的Deep Learning(DL)做法。当然,在RL中确实是这么做的。
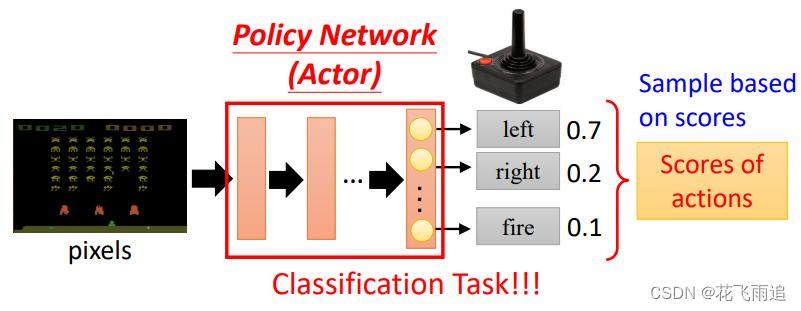
有了可训练的网络模型,就需要定义"Loss Function"用于训练。不同的是DL是为了使结果更加精准,需要尽可能的减小Loss,是一个“下山”的过程,而RL是为了尽可能的增大奖励,是一个“上山”的过程。奖励可以根据动作和状态计算,例如下图中击杀怪物后会获得一定量的分数。
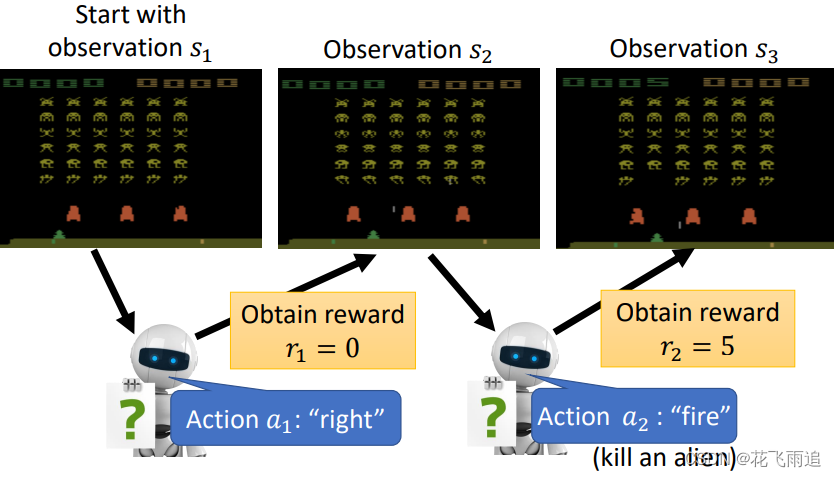
让模型不断产生动作直到游戏结束,这就是一轮次(episode)(类似于DL中的epoch),那么我们可以把所有的奖励累加起来。一个简单的思路是可以利用奖励和去更新Neural Network的权重。
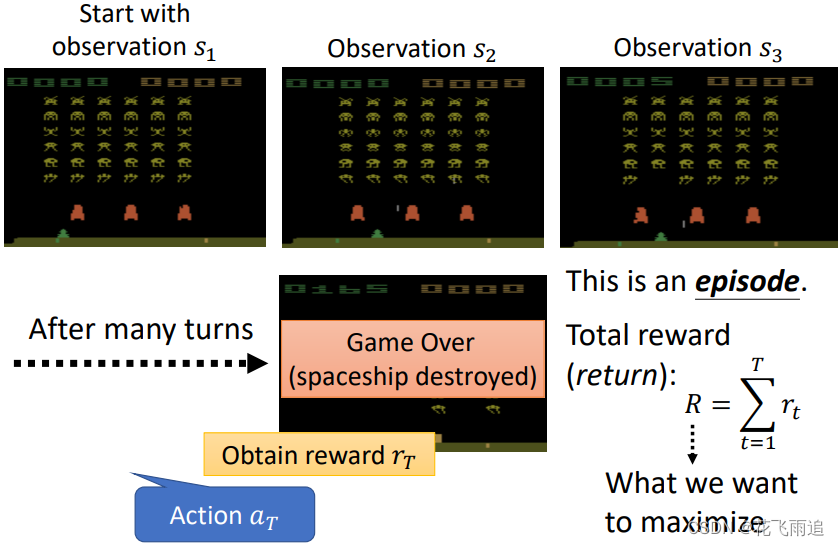
定义:一次episode的奖励总和为 R = ∑ t = 1 T r t R=\sum_{t=1}^{T}{r_t} R=∑t=1Trt ,总共进行 T T T 次动作, r t r_t rt 为第 t t t 次动作 a t a_t at 产生的奖励。现在需要训练Neural Network使 R R R 最大化,这就需要一个优化策略。
2.2 Policy Gradient详解
怎么知道这个动作好还是不好呢?可以让Actor实际的去“玩”一下游戏。假设动作 π θ ( s ) \pi_\theta(s) πθ(s) 的参数是 θ \theta θ ,就让Actor π θ ( s ) \pi_\theta(s) πθ(s) 反复去玩这个游戏。那么经过不断“玩”,可以得到总得分为 R θ R_\theta Rθ 。就算是在同一个环境下采取相同的Action,得到的 R θ R_\theta Rθ 也会不相同,这是因为Actor具有一定的随机性。那么我们需要尽可能大的去增加总奖励的期望 R ˉ θ \bar R_\theta Rˉθ ,而不是某一次的结果增大。

定义:一次episode的所有状态、动作、奖励组成的向量叫 τ \tau τ ,其代表一次episode的过程,相关公式如下:
τ = { s 1 , a 1 , r 1 , s 2 , a 2 , r 2 , . . . , s T , a T , r T } \tau = \{s1, a1, r1, s2, a2, r2, ..., s_T, a_T, r_T\} τ={s1,a1,r1,s2,a2,r2,...,sT,aT,rT}R ( τ ) = ∑ n = 1 N r n R(\tau)=\sum_{n=1}^{N}r_n R(τ)=n=1∑Nrn
假设对于一个Actor,每一种过程 τ \tau τ 都可能被列举到,每一种 τ \tau τ 出现的概率取决于Actor的参数 θ \theta θ ,定义为 P ( τ ∣ θ ) P(\tau|\theta) P(τ∣θ) 。那么 R ˉ θ \bar R_\theta Rˉθ 就等于每一次episode中的得分 R θ R_\theta Rθ 与该过程 τ \tau τ 出现的几率的乘积之和,见如下公式:
R ˉ θ = ∑ τ R ( τ ) P ( τ ∣ θ ) ≈ 1 N ∑ n = 1 N R ( τ n ) \bar R_\theta=\sum_{\tau}{R(\tau)P(\tau|\theta)}\approx\frac{1}{N}\sum_{n=1}^N{R(\tau^n)} Rˉθ=τ∑R(τ)P(τ∣θ)≈N1n=1∑NR(τn)
但 τ \tau τ 的情况太复杂了,难以枚举所有情况,可以让 π θ \pi_\theta πθ sample N N N 次,得到 { τ 1 , τ 2 , . . . , τ N } \{\tau^1, \tau^2, ..., \tau^N\} {τ1,τ2,...,τN} 与所有的出现概率 P ( τ ∣ θ ) P(\tau|\theta) P(τ∣θ) 。那么问题就变成了如下表达式:
θ ∗ = arg max θ R ˉ θ , R ˉ θ = ∑ τ R ( τ ) P ( τ ∣ θ ) \theta^{*}=\arg \max _{\theta} \bar{R}_{\theta}, \bar{R}_{\theta}=\sum_{\tau}R(\tau)P(\tau|\theta) θ∗=argθmaxRˉθ,Rˉθ=τ∑R(τ)P(τ∣θ)
由前文中提到RL的训练过程是一个“上山”的过程,所以可以用Gradient Ascent。2.2.1 Gradient Ascent
需要更新的权重为 θ \theta θ ,梯度的方向为 ∇ R ˉ θ \nabla \bar R_\theta ∇Rˉθ 。

根据 R ˉ θ = ∑ τ R ( τ ) P ( τ ∣ θ ) \bar{R}_{\theta}=\sum_{\tau}R(\tau)P(\tau|\theta) Rˉθ=∑τR(τ)P(τ∣θ) ,其中 R ( τ ) R(\tau) R(τ) 由于其有一定的随机性,只需要把 τ \tau τ 放进去根据 R ( ⋅ ) R(·) R(⋅) 得到结果,可以把其看成一个完全的“黑盒子”,不用考虑其可微性质。这样考虑的具体原因是 R ( τ ) R(\tau) R(τ) 本身是由环境打分得到的,环境是一个“黑盒子”。那么 ∇ R θ \nabla R_{\theta} ∇Rθ 为:
∇ R θ = ∑ τ R ( τ ) ∇ P ( τ ∣ θ ) = ∑ τ R ( τ ) P ( τ ∣ θ ) ∇ P ( τ ∣ θ ) P ( τ ∣ θ ) \nabla R_\theta = \sum_{\tau}{R(\tau)\nabla P(\tau|\theta)} = \sum_{\tau}{R(\tau)P(\tau|\theta)\frac{\nabla P(\tau|\theta)}{P(\tau|\theta)}} ∇Rθ=τ∑R(τ)∇P(τ∣θ)=τ∑R(τ)P(τ∣θ)P(τ∣θ)∇P(τ∣θ)
又由于:
d l o g ( f ( x ) ) d x = 1 f ( x ) d f ( x ) d x \frac{dlog(f(x))}{dx}=\frac{1}{f(x)} \frac{df(x)}{dx} dxdlog(f(x))=f(x)1dxdf(x)∇ l o g ( f ( x ) ) = ∇ f ( x ) f ( x ) \nabla log(f(x))=\frac{\nabla f(x)}{f(x)} ∇log(f(x))=f(x)∇f(x)
那么 ∇ R θ \nabla R_\theta ∇Rθ 可以变为:
∇ R θ = ∑ τ R ( τ ) P ( τ ∣ θ ) ∇ l o g P ( τ ∣ θ ) ≈ 1 N ∑ n = 1 N R ( τ n ) ∇ l o g P ( τ n ∣ θ ) \nabla R_\theta = \sum_{\tau}{R(\tau)P(\tau|\theta)\nabla log P(\tau|\theta)} \approx \frac{1}{N}\sum^{N}_{n=1}{R(\tau^n)\nabla log P(\tau^n|\theta)} ∇Rθ=τ∑R(τ)P(τ∣θ)∇logP(τ∣θ)≈N1n=1∑NR(τn)∇logP(τn∣θ)其中 “玩” N N N 次游戏得到 { τ 1 , τ 2 , . . . , τ N } \{\tau^1, \tau^2, ..., \tau^N\} {τ1,τ2,...,τN} ,假设 N N N 足够大,表示概率的部分 P ( τ ∣ θ ) P(\tau|\theta) P(τ∣θ) 就可以直接利用平均数去掉。现在的问题变成了如何计算 ∇ l o g P ( τ ∣ θ ) \nabla log P(\tau|\theta) ∇logP(τ∣θ) 。
我们可以把 P ( τ ∣ θ ) P(\tau|\theta) P(τ∣θ) 展开:
P ( τ ∣ θ ) = p ( s 1 ) p ( a 1 ∣ s 1 , θ ) p ( r 1 , s 2 ∣ s 1 , a 1 ) p ( a 2 ∣ s 2 , θ ) p ( r 2 , s 3 ∣ s 2 , a 2 ) ⋯ = p ( s 1 ) ∏ t = 1 T p ( a t ∣ s t , θ ) p ( r t , s t + 1 ∣ s t , a t ) P(\tau|\theta)= p\left(s_{1}\right) p\left(a_{1} \mid s_{1}, \theta\right) p\left(r_{1}, s_{2} \mid s_{1}, a_{1}\right) p\left(a_{2} \mid s_{2}, \theta\right) p\left(r_{2}, s_{3} \mid s_{2}, a_{2}\right) \cdots =p(s_1)\prod^{T}_{t=1}{p(a_t|s_t, \theta)p(r_t, s_{t+1}|s_t, a_t)} P(τ∣θ)=p(s1)p(a1∣s1,θ)p(r1,s2∣s1,a1)p(a2∣s2,θ)p(r2,s3∣s2,a2)⋯=p(s1)t=1∏Tp(at∣st,θ)p(rt,st+1∣st,at)
其实这是一个用于描述马尔科夫决策过程的公式,其中每个状态和行动都有相应的概率分布。其中 p ( s 1 ) p(s_1) p(s1) 与 p ( r t , s t + 1 ∣ s t , a t ) p(r_t, s_{t+1}|s_t, a_t) p(rt,st+1∣st,at) 跟 π θ \pi_\theta πθ 是没关系的, p ( a t ∣ s t , θ ) p(a_t|s_t, \theta) p(at∣st,θ) 受 π θ \pi_\theta πθ 控制,后者的解释可以见下图。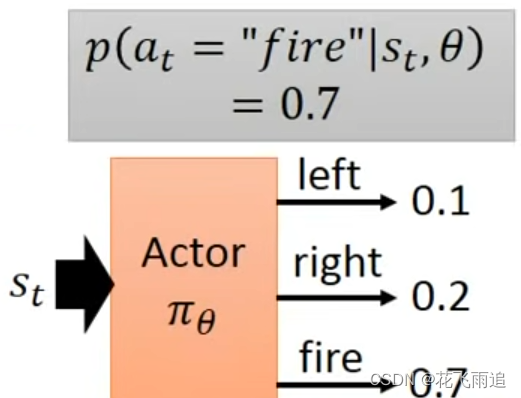
那么 l o g P ( τ ∣ θ ) logP(\tau|\theta) logP(τ∣θ) 可以变成如下:
l o g P ( τ ∣ θ ) = l o g p ( s 1 ) + ∑ t = 1 T l o g p ( a t ∣ s t , θ ) + l o g p ( r t , s t + 1 ∣ s t , a t ) logP(\tau|\theta) = logp(s_1)+\sum_{t=1}^{T}logp(a_t|s_t, \theta) + logp(r_t, s_{t+1}|s_t, a_t) logP(τ∣θ)=logp(s1)+t=1∑Tlogp(at∣st,θ)+logp(rt,st+1∣st,at)
则 ∇ l o g P ( τ ∣ θ ) \nabla log P(\tau|\theta) ∇logP(τ∣θ) 跟 π θ \pi_\theta πθ 不相干的项直接可以去掉了,变成如下式子:
∇ l o g P ( τ ∣ θ ) = ∑ t = 1 T ∇ l o g p ( a t ∣ s t , θ ) \nabla logP(\tau|\theta)=\sum_{t=1}^{T}\nabla logp(a_t|s_t, \theta) ∇logP(τ∣θ)=t=1∑T∇logp(at∣st,θ)
那么可以把这个式子往回带,就可以得到 ∇ R ˉ θ \nabla \bar R_\theta ∇Rˉθ (注意这里的 T T T 变成了 T n T_n Tn ,这是因为对于不同的 τ \tau τ 产生动作序列的次数不一样,所以需要添加下标 n n n 与 不同轮次的 τ \tau τ 对应):
∇ R ˉ θ ≈ 1 N ∑ n = 1 N R ( τ n ) ∇ l o g P ( τ n ∣ θ ) = 1 N ∑ n = 1 N R ( τ n ) ∑ t = 1 T n ∇ l o g p ( a t n ∣ s t n , θ ) = 1 N ∑ n = 1 N ∑ t = 1 T n R ( τ n ) ∇ l o g p ( a t n ∣ s t n , θ ) \nabla \bar R_\theta \approx \frac{1}{N} \sum_{n=1}^{N}{R(\tau^n) \nabla log P(\tau^n|\theta)} = \frac{1}{N} \sum_{n=1}^{N}{R(\tau^n) \sum_{t=1}^{T_n}{\nabla log p(a_t^n|s_t^n, \theta)}} = \frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_n}{R(\tau^n){\nabla log p(a_t^n|s_t^n, \theta)}} ∇Rˉθ≈N1n=1∑NR(τn)∇logP(τn∣θ)=N1n=1∑NR(τn)t=1∑Tn∇logp(atn∣stn,θ)=N1n=1∑Nt=1∑TnR(τn)∇logp(atn∣stn,θ)
这个式子的含义是,假设在sample的一个 θ \theta θ 里面, s t n s_t^n stn 这个State下采取了 a t n a_t^n atn 这个动作的概率,取log再计算梯度,与那一次 τ \tau τ 的总奖励相乘。进一步理解,如果在某一次 τ n \tau^n τn 时,机器在看到状态 s t n s_t^n stn 时,采取了一个动作 a t n a_t^n atn ,然后总的奖励是正的,那么机器就会自己去增加看到这个场景下做出该行动的概率。
值得注意的是,如果把梯度里的 R ( τ n ) R(\tau^n) R(τn) 替换成 r t n r_t^n rtn 后,也就是将第 n n n 次 τ n \tau^n τn 的总奖励换成第 n n n 次 τ n \tau^n τn 在 t t t 时刻在状态 s t n s_t^n stn 下采取动作 a t n a_t^n atn 得到的奖励,那么就会丢失其他动作的期望贡献,最后训练出来的模型只会在原地开火。这里还能这么理解(个人理解),如果换成 r t n r_t^n rtn ,由于sample的随机性,可以不用考虑 1 N ∑ n = 1 N \frac{1}{N}\sum_{n=1}^{N} N1∑n=1N 这一层。那么 ∇ R ˉ θ \nabla \bar R_\theta ∇Rˉθ 可以写成:
∇ R ˉ θ = g ( ∑ t = 1 T r t ∇ l o g p ( a t ∣ s t , θ ) ) \nabla \bar R_\theta = g(\sum_{t=1}^{T}r_t \nabla log p(a_t|s_t, \theta)) ∇Rˉθ=g(t=1∑Trt∇logp(at∣st,θ))
此时的 r t r_t rt 与 a t , s t a_t, s_t at,st 唯一对应,那么梯度在每个时刻只关注了一个动作的奖励与概率,很容易陷入局部最优,导致训练出来的模型在某一特定环境下只会侧重一个动作。由Actor在不同连续的 s t s_t st 下产生的一系列动作是有一定的关联性的,类似于NLP上下文特征或者音频里的时域特征,所以不能只考虑某一 a t , s t a_t, s_t at,st 下单独的 r t r_t rt。这就有点类似于分类任务的损失函数。有了梯度,就可以根据Gradient Ascent更新Actor网络的权重,公式如下:
θ n e w ← θ o l d + η ∇ R ˉ θ o l d \theta^{new} ← \theta^{old} + \eta \nabla \bar R_{\theta^{old}} θnew←θold+η∇Rˉθold
下面我们再看看更新模型的过程,如下图,即生成一组训练数据,更新一次 θ \theta θ ,值得注意的是每一组训练数据只能用一次。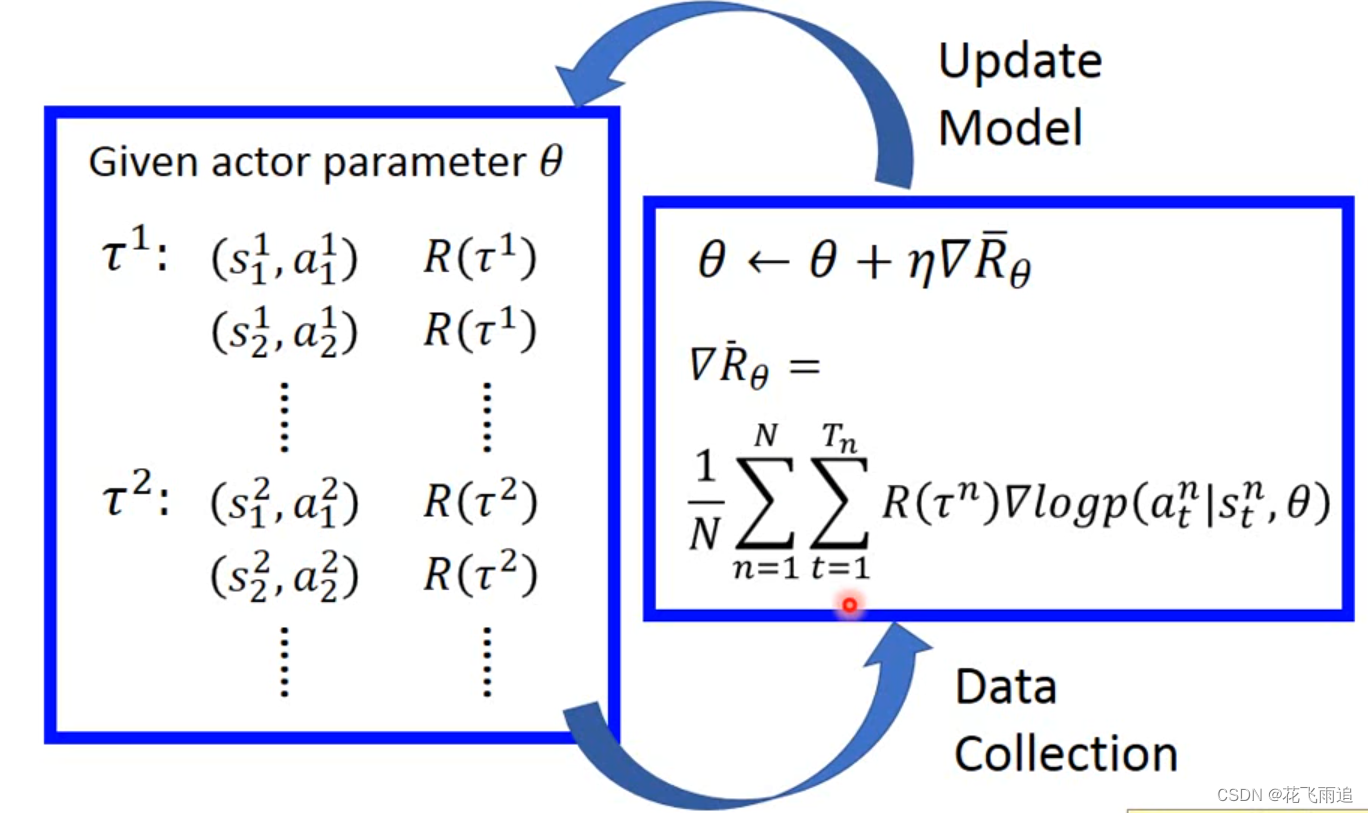
2.2.2 如何损失函数进一步优化
假设所有的 R ( τ n ) R(\tau^n) R(τn) 都是正值。假设在某一个状态下,采取 a , b , c a, b, c a,b,c 三个动作的概率如下,但 a , c a, c a,c 的奖励更高,那么理想状态下经过训练 a , c a, c a,c 出现的概率会增高, b b b 出现的概率会降低。但实际上我们是sample的,假设没有采集到 a a a 动作这种情况,那么经过训练后 a a a 出现的概率会降低。这时,我们需要引入一个baseline,即可以对 R ( τ n ) R(\tau^n) R(τn) 减去一个 b b b ,从而使奖励有好有坏,不然都是正值无法区分,通常可以将 b b b 值设置为与 R ( τ n ) R(\tau^n) R(τn) 的期望接近的值,即 E [ R ( τ n ) ] E[R(\tau^n)] E[R(τn)]。
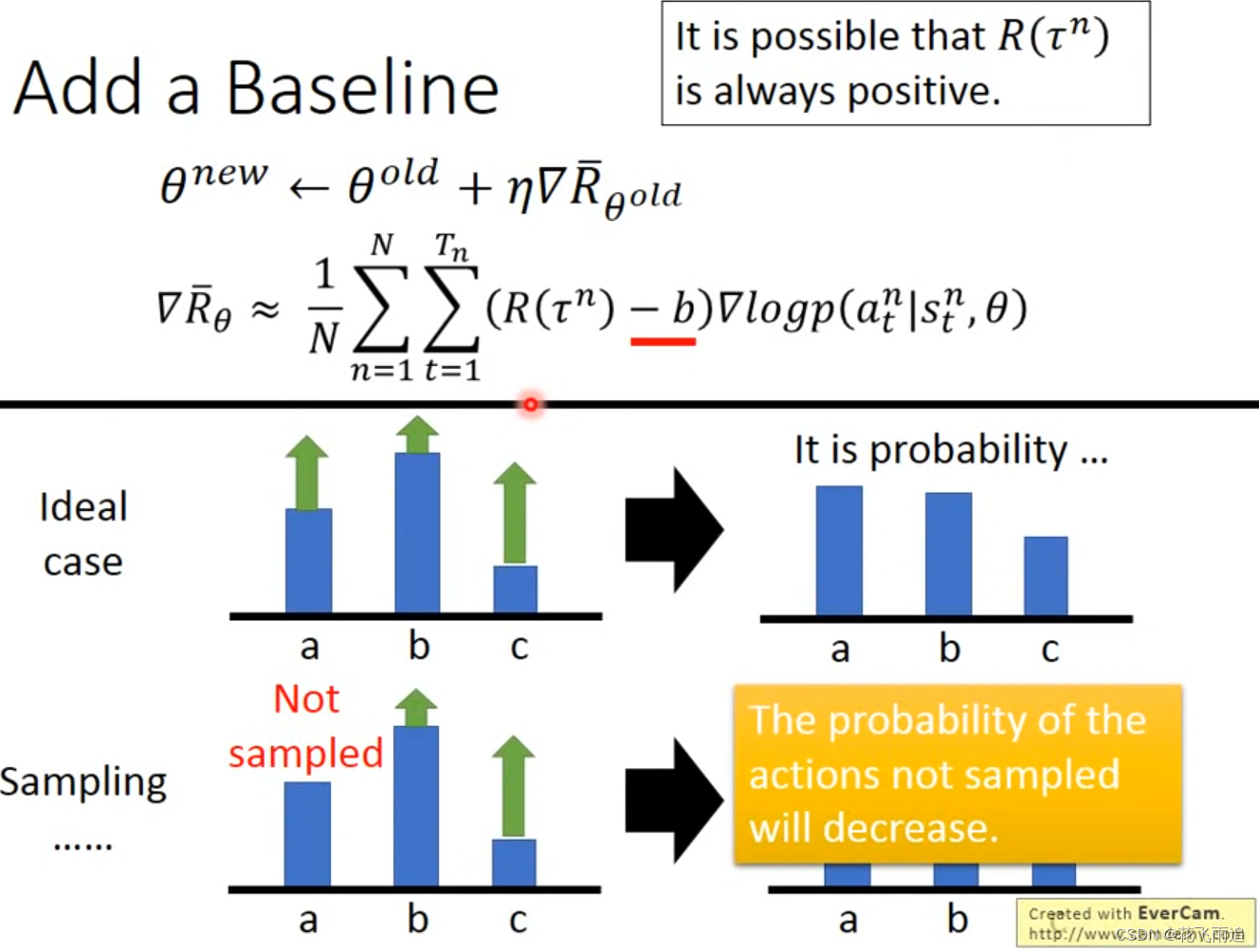
还有很多方法能缓解这一问题,例如为不同的动作分配不同的权重,即好的动作给正分,差的动作给负分,再将 R ( τ n ) R(\tau^n) R(τn) 替换成所有动作的权重和,这种做法的本质就是改变了原本奖励的计算。

随着时间的推移,状态-动作的组合会越来越多,那么前面的组合对距离过远的组合的影响就会越来越小,可以用添加一个衰减因子 γ \gamma γ ,这种方法叫Advantage function,见下图。
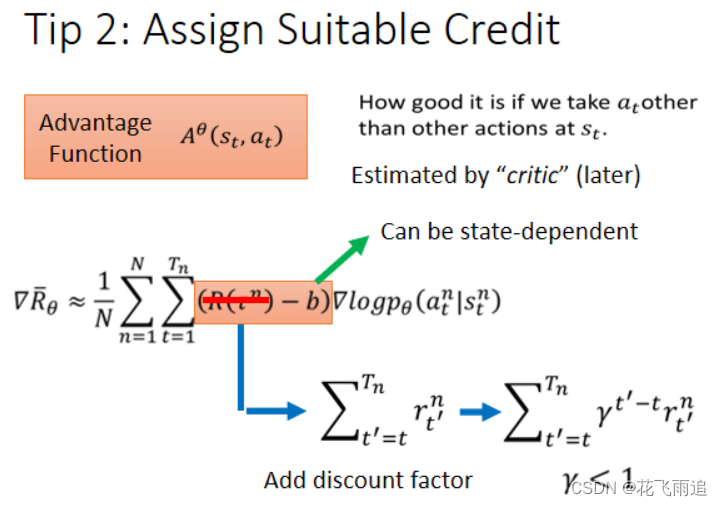
-
相关阅读:
进程的调度算法
mysql8.0英文考试第1-5题
故障分析 | MySQL Router:服务器后端那么闲,为什么不让访问?
【程序人生】上海城市开发者社区小聚有感
c++builder 6.0 使用TRichView最基本的方法
Vue ref属性
TCP/IP 详解(第 2 版) 笔记 / 3 链路层 / 3.5 无线局域网 - IEEE 802.11 (Wi-Fi) / 3.5.5 Wi-Fi 安全
【小程序项目开发-- 京东商城】uni-app之自定义搜索组件(中)-- 搜索建议
通俗理解ABP中的模块Module
骨传导耳机怎么听到声音?骨传导耳机是否会对听力造成损害?
- 原文地址:https://blog.csdn.net/qq_36258516/article/details/133822467