-
论文导读|八月下旬Operations Research文章精选:定价问题专题

编者按:
在“ Operations Research论文精选”中,我们有主题、有针对性地选择了Operations Research中一些有趣的文章,不仅对文章的内容进行了概括与点评,而且也对文章的结构进行了梳理,旨在激发广大读者的阅读兴趣与探索热情。在本期“论文精选”中,我们以“定价问题”为主题,涉及动态定价问题、马尔可夫均衡,未知非参数模型、机器学习、迭代贪心等诸多知识。推荐文章1
● 题目:Strategic Pricing in Volatile Markets
波动市场中的策略定价
● 期刊:Operations Research
● 原文链接:https://doi.org/10.1287/opre.2021.0550
● 作者:Sebastian Gryglewicz, Aaron Kolb
● 关键词:limit pricing(限制定价) • market entry(市场进入)• signaling (信号)• optimal stopping (最优停止)• stochastic games(随机游戏)
● 摘要:
We study dynamic entry deterrence through limit pricing in markets subject to persistent demand shocks. An incumbent is privately informed about its costs, high or low, and can deter a Bayesian potential entrant by setting its prices strategically. The entrant can irreversibly enter the market at any time for a fixed cost, earning a payoff that depends on the market conditions and the incumbent’s unobserved type. Market demand evolves as a geometric Brownian motion. When market demand is low, entry becomes a distant threat, so there is little benefit to further deterrence, and, in equilibrium, a weak incumbent becomes tempted to reveal itself by raising its prices. We characterize a unique equilibrium in which the entrant enters when market demand is sufficiently high (relative to the incumbent’s current reputation), and the weak incumbent mixes over revealing itself when market demand is sufficiently low. In this equilibrium, pricing and entry decisions exhibit path dependence, depending not only on the market’s current size, but also its historical minimum.
我们通过持续需求冲击下的市场限制定价来研究动态进入者威慑(dynamic entry deterrence)。在位者私下知道自己的成本是高是低,并可以通过战略性地设定价格来阻止贝叶斯理论的潜在进入者。进入者可以在任何时间以固定成本不可逆转地进入市场,获得的回报取决于市场条件和在位者的未观察类型。市场需求演变为一个几何布朗运动。当市场需求较低时,潜在进入者基本不构成威胁,因此进一步的威慑几乎没有什么好处,而且,在均衡状态下,弱势的在位者会试图通过提高价格来暴露自己。我们描述了一种独特的均衡,在这种均衡中,当市场需求足够高时(相对于在位者目前的声誉),进入者进入,而当市场需求足够低时,弱势在位者混合在一起,过度暴露自己。在这个均衡中,定价和进入决策表现出路径依赖,不仅取决于市场当前的规模,还取决于其历史最小值。
● 文章结构:

● 点评:
本文对于市场在位者和潜在进入者的动态均衡问题进行了研究。提出了一个基于马尔可夫均衡的(U,L)模型,也对该模型其他功能的拓展进行了简要概述。本文研究结果表明,经济衰退后进入延迟,导致经济复苏缓慢,在位者在经济衰退中幸存下来的可能性更大。为市场进入威慑提出了新的研究思路。推荐文章2
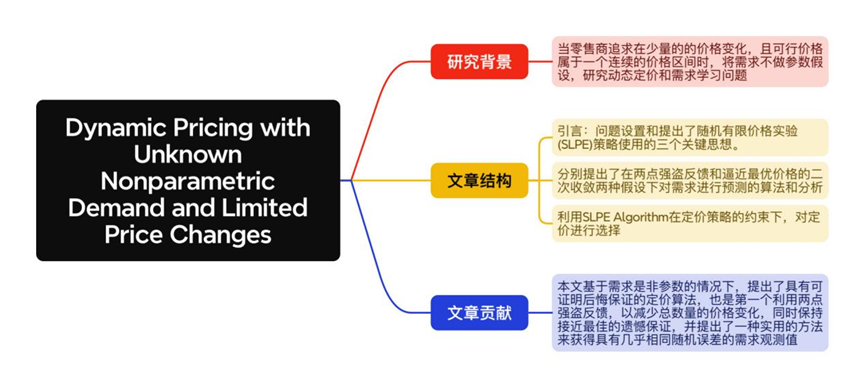
● 题目:Dynamic Pricing with Unknown Nonparametric Demand and Limited Price Changes
未知非参数需求和有限价格变动的动态定价
● 期刊:Operations Research
● 原文链接:https://doi.org/10.1287/opre.2020.0445
● 作者:Georgia Perakis, Divya Singhvi
● 关键词:learning(学习 )• dynamic pricing(动态定价) • nonparametric models(非参数模型) • limited price changes(有限价格变化)
● 摘要:
We consider the dynamic pricing problem of a retailer who does not have any information on the underlying demand for a product. The retailer aims to maximize cumulative revenue collected over a finite time horizon by balancing two objectives: learning demand and maximizing revenue. The retailer also seeks to reduce the amount of price experimentation because of the potential costs associated with price changes. Existing literature solves this problem in cases where the unknown demand is parametric. We consider the pricing problem when demand is nonparametric. We construct a pricing algorithm that uses second order approximations of the unknown demand function and establish when the proposed policy achieves near-optimal rate of regret, O ~ ( T ) \widetilde{O}(\sqrt T) O (T)while making O ( l o g l o g T ) O(log\ logT) O(log logT)price changes. Hence, we show considerable reduction in price changes from the previously known o ( l o g T ) o(log\ T) o(log T) rate of price change guarantee in the literature. We also perform extensive numerical experiments to show that the algorithm substantially improves over existing methods in terms of the total price changes, with comparable performance on the cumulative regret metric.
我们研究了不知道产品任何潜在需求信息的零售商动态定价问题。零售商的目标是通过平衡两个目标:了解需求和最大化收入,在有限的时间范围内最大化累积收入。零售商还力求减少价格试验的数量,因为价格变化具有潜在成本。现有文献在未知需求为参数的情况下解决了这一问题。考虑需求是非参数时的定价问题。我们构建了一个定价算法,该算法使用未知需求函数的二阶近似,并确定所提出的策略何时达到接近最优的后悔率 O ~ ( T ) \widetilde{O}(\sqrt T) O (T)同时进行 O ( l o g l o g T ) O(log\ logT) O(log logT)价格变化。因此,与之前文献显示的 o ( l o g T ) o(log\ T) o(log T)价格变化了相比,我们在价格试验次数上展现了相当大的减少,我们还进行了大量的数值实验,以表明该算法在总价格变化方面大大改进了现有方法,在累积遗憾度量上具有相当好的性能。
● 文章结构:
● 点评:
本文研究了当潜在需求未知且非参数,以实现价格设置恰当的同时减少定价试验次数为目的,零售商销售单一产品的动态定价问题。文章构建了一个动态定价策略,该策略使用非参数需求的二阶近似来生成未来价格。提出的政策在分析和数值上都表现良好。为零售商在新产品定价问题上提出了切实有效的办法,达到减少成本、收入最大化的目的。推荐文章3
● 题目:Dynamic Pricing and Learning with Discounting
动态定价与折扣学习
● 期刊:Operations Research
● 原文链接:https://doi.org/10.1287/opre.2023.2477
● 作者:Zhichao Feng, Milind Dawande, Ganesh Janakiraman, Anyan Qi
● 关键词:dynamic pricing(动态定价) • learning(学习) • discounting (折扣)• regret minimization(遗憾最小化)
● 摘要:
In many practical settings, learning algorithms can take a substantial amount of time to converge, thereby raising the need to understand the role of discounting in learning. We illustrate the impact of discounting on the performance of learning algorithms by examining two classic and representative dynamic-pricing and learning problems studied in Broder and Rusmevichientong (BR) [Broder J, Rusmevichientong P (2012) Dynamic pricing under a general parametric choice model. Oper. Res. 60(4):965–980] and Keskin and Zeevi (KZ) [Keskin NB, Zeevi A (2014) Dynamic pricing with an unknown demand model: Asymptotically optimal semi-myopic policies. Oper. Res. 62(5):1142–1167]. In both settings, a seller sells a product with unlimited inventory over T periods. The seller initially does not know the parameters of the general choice model in BR (respectively, the linear demand curve in KZ). Given a discount factor ρ, the retailer’s objective is to determine a pricing policy to maximize the expected discounted revenue over T periods. In both settings, we establish lower bounds on the regret under any policy and show limiting bounds of Ω ( 1 / ( 1 − ρ ) ) Ω(\sqrt {1/(1 - \rho )} ) Ω(1/(1−ρ))and Ω ( T ) Ω(\sqrt T) Ω(T)and when T →∞ and $\rho $→1, respectively. In the model of BR with discounting, we propose an asymptotically tight learning policy and show that the regret under our policy as well that under the MLE-CYCLE policy in BR is O ( 1 / ( 1 − ρ ) ) O(\sqrt {1/(1 - \rho )} ) O(1/(1−ρ))(respectively, O ( T ) O(\sqrt T) O(T))when T →∞ (respectively, $\rho $→1).In the model of KZ with discounting, we present sufficient conditions for a learning policy to guarantee asymptotic optimality and show that the regret under any policy satisfying these conditions is O ( l o g ( 1 / 1 − ρ ) 1 / ( 1 − ρ ) ) O(log(1/1-\rho)\sqrt {1/(1 - \rho )}) O(log(1/1−ρ)1/(1−ρ))(respectively, O ( l o g T T ) O(logT\sqrt T) O(logTT)when T →∞(respectively, $\rho $→1).We show that three different policies—namely, the two variants of the greedy iterated least squares policy in KZ and a different policy that we propose—achieve this upper bound on the regret. We numerically examine the behavior of the regret under our policies as well as those in BR and KZ in the presence of discounting. We also analyze a setting in which the discount factor per period is a function of the number of decision periods in the planning horizon.在许多实际设置中,学习算法可能需要大量的时间来收敛,因此需要了解贴现在学习中的作用。我们通过考察Broder和Rusmevichientong (BR) 研究的两个经典且具有代表性的动态定价和学习问题来说明折扣对学习算法性能的影响[Broder J, Rusmevichientong P (2012) Dynamic pricing under a general parametric choice model. Oper. Res. 60(4):965–980] ,还有 Keskin and Zeevi (KZ) [Keskin NB, Zeevi A (2014) Dynamic pricing with an unknown demand model: Asymptotically optimal semi-myopic policies. Oper. Res. 62(5):1142–1167]. 在这两种情况下,卖家在T个周期内销售具有无限库存的产品。卖方最初不知道BR中一般选择模型的参数(或KZ中的线性需求曲线)。给定折扣系数ρ,零售商的目标是确定一种定价策略,使T期间的预期折扣收入最大化。在这两种情况下,我们建立了任何策略下的后悔下界,并分别给出了当T→∞和ρ→1时, Ω ( 1 / ( 1 − ρ ) ) Ω(\sqrt {1/(1 - \rho )} ) Ω(1/(1−ρ))和 Ω ( T ) Ω(\sqrt T) Ω(T)的极限界。在有折扣的BR模型中,我们提出了一种渐近紧密学习策略,并证明了在我们的策略下以及在BR的MLE-CYCLE策略下的遗憾是 O ( 1 / ( 1 − ρ ) ) O(\sqrt {1/(1 - \rho )} ) O(1/(1−ρ))(或 O ( T ) O(\sqrt T) O(T))当T→∞(或ρ→1)时。我们给出了一个学习策略保证渐近最优性的充分条件,并证明了在满足这些条件的任何策略下的后悔是 O ( l o g ( 1 / 1 − ρ ) 1 / ( 1 − ρ ) ) O(log(1/1-\rho)\sqrt {1/(1 - \rho )}) O(log(1/1−ρ)1/(1−ρ))(或 O ( l o g T T ) O(logT\sqrt T) O(logTT)),当T→∞(或ρ→1)时。我们证明了三种不同的策略-即,KZ中贪婪迭代最小二乘策略的两个变体和我们提出的另一个策略实现了遗憾的上界。我们在数字上检验了我们的政策下的后悔行为,以及BR和KZ中存在折扣的行为。我们还分析了一种设定,其中每个周期的贴现因子是规划范围内决策周期数量的函数。
● 文章结构:

● 点评:
本文通过研究BR和KZ研究的两个经典和代表性的动态定价和学习问题,研究了折扣对学习算法性能的影响。并研究了如何将折扣纳入CILS等算法中,同时进行探索和利用。本文中的分析在理解非平稳需求如何影响动态定价和存在折扣的需求学习做出了很大的贡献。 -
相关阅读:
追风者变引领者:Horwin的技术攀爬
我的 ReactNative 开发利器: 常用命令总结
ubuntu 20.04+ORB_SLAM3 安装配库教程
数据结构--串的基本概念
1、如何抓取Modbus TCP/UDP 数据包实战
第七章:java Object类
数据仓库概念梳理
LORA详解
装饰器模式
永续资金费率说明
- 原文地址:https://blog.csdn.net/weixin_53463894/article/details/133819253