课题学习(六)----安装误差校准、实验方法

一、 安装误差校准

1.1 数学模型

   在实际情况下，即使努力尝试使三轴加速度计和三轴磁通门正交，也不可能保证坐标轴的正交和安装的准确居中。无论采用何种解法，都会导致最终解的误差。因此，要想提高测量精度，就必须开发一种补偿算法，使传感器居中且相互正交，即从系统的数学模型出发，设计相应的算法求解出安装误差，并准确计算出钻柱姿态。
   由于安装误差不可避免，需要通过实验室实验获得校准参数，因此我们尝试建立误差补偿的算法模型。首先，假设在建立数学模型之前，Ax、Ay、Az为加速度计的输出电压，则重力各分量与输出电压的关系如下式所示：

   $K_{ix},K_{iy}，K_{iz}$表示三轴加速度校准系数。
   我们假设$I_{Ax},I_{Ay},I_{Az}$和$T_{Ax},T_{Ay},T_{Az}$表示三轴加速度计安装角和相位的安装角，可以得到下式：

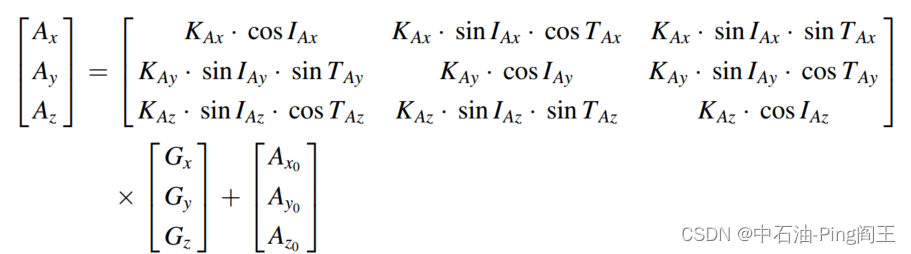
   对比上面两式，可以很容易的得到$$K_{xx}=K_{Ax}\cdot cos{I}_{Ax},...,K_{zz}=K_{Az}\cdot cos{I}_{Az}$$
   由此，我们可以计算出加速度计的校准系数为和传感器偏差：

   对于安装在x轴上的加速度计，定义$cos(AxPx)、cos(AxPy)$和$cos(AxPz)$为加速度计敏感轴与仪器坐标系三轴夹角的余弦值：
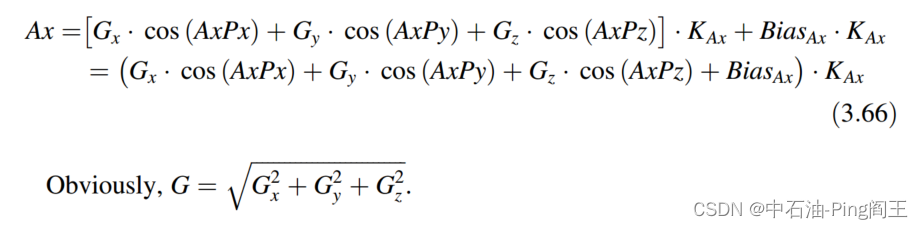
   然后给出加速度计误差标定的数学模型:

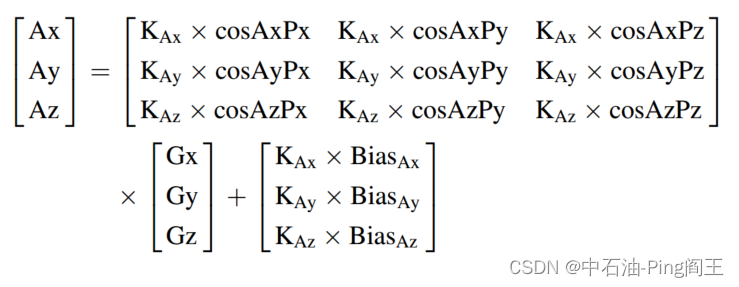
   同理，得到磁通门误差标定数学模型如式
   然后在算法中使用校准参数$K_{Ai}，Bia{s}_{Ai}，cos(A_i{P}_j)，L_{Fi},Bia{s}_{Fi}，cos(F_i{P}_j)L_{Fx}$,其中，$i=x,y,z,j=x,y,z$，带入算法之后便可以得到校准之后的值。

1.2实验方法

   设计可放置在三维空间任意位置的实验仪器，并采用非磁性材料，保证磁通门传感器不受干扰。

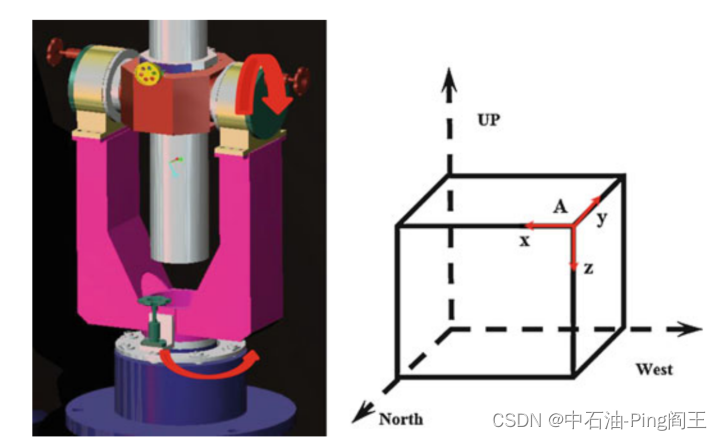
  首先采用正交法标定安装误差。确定下表所示的24个位置，计算每个点的倾角和方位角值即可得到校正参数。如上图右侧所示，A点代表表1中的数字2。


  以Ax为例，由加速度计误差标定的数学模型可得公式如下:$$K_{Ax}\times cos{A}_x{P}_x\times G_x=\frac{1}{8}(A_{x1}+A_{x5}+A_{x18}+A_{x24}-A_{x3}-A_{x7}-A_{x20}-A_{22})...$$

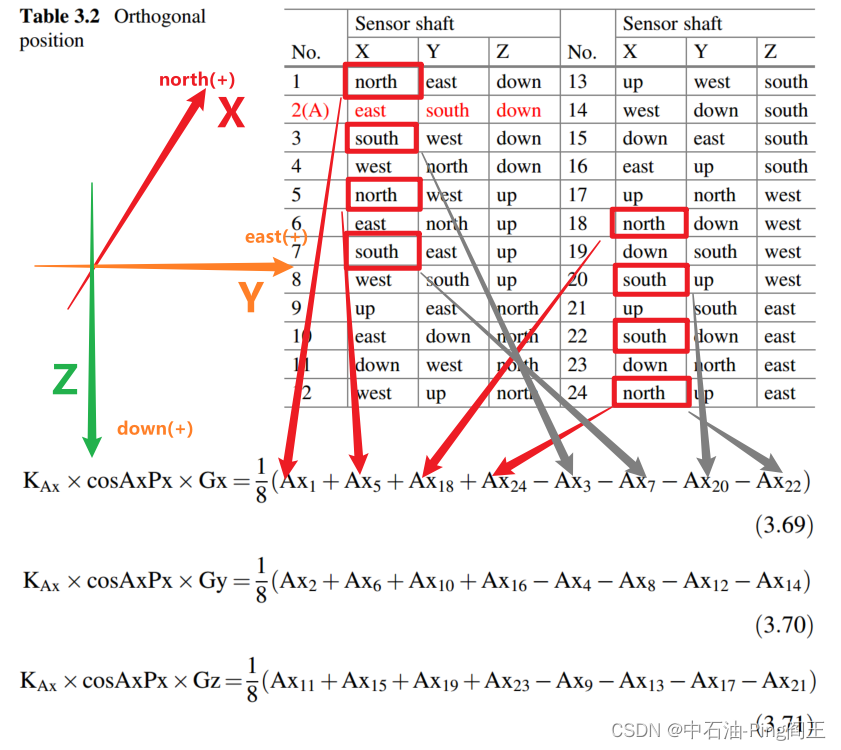
  注意，上式中有一些错误：


  上图中,$G_{hc}=G\cdot cos{A}_x{P}_x,G_{hs}=G\cdot cos{A}_x{P}_y,G_v=G\cdot cos{A}_x{P}_z$(个人推测，原论文中作者并未说明，但是可以倒推出来)。
  但采用正交法标定系统所需仪器不仅精度高，而且结构复杂。由于实际应用比较困难，我们提出了数据拟合的方法。具体步骤如下：
  将仪器固定在一个位置(固定井斜和方位)，旋转360°。仪器旋转45°(误差:±1°)采样一次数据，仪器旋转360°将采样8次数据。利用基于正交三角函数的数值拟合理论，可以得到仪器旋转360°时的传感器输出电压曲线。然后计算每个传感器的标定系数。
  以Ax和Fx为例介绍了计算方法：$$A_x=(G_x\cdot cos{A}_x{P}_x+G_y\cdot cos{A}_x{P}_y+G_z\cdot cos{A}_x{P}_z+Bia{s}_{Ax})K_{Ax}$$
$$F_x=(B_x\cdot cos{A}_x{P}_x+B_y\cdot cos{A}_x{P}_y+B_z\cdot cos{A}_x{P}_z+Bia{s}_{Ax})L_{Fx}$$
  然后：$$A_x=K_{Ax}\cdot G\cdot sinI\cdot cos{A}_x{P}_x\cdot cosT-K_{Ax}\cdot G\cdot sinI\cdot cos{A}_x{P}_y\cdot sinT+K_{Ax}\cdot (-G\cdot cosI\cdot cos{A}_x{P}_z+Bia{s}_{Ax})$$
  假设如下：

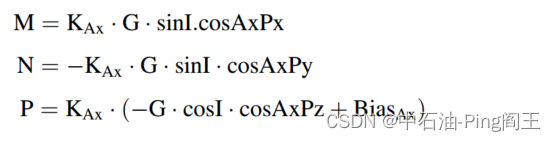
  加入倾角不变，则M,N,P均为常数，带入下式
$$A_x=M\cdot cosr+N\cdot sinr+P$$
$$F_x=m\cdot cosr+n\cdot sinr+p$$
  上面两式就是加速度计和磁通门的输出数学模型，其中，
  为了达到更高的拟合精度，选择正交三角函数作为基本函数来拟合各传感器的输出曲线。还是$A_x$为例，假设$A_m={\alpha }_0,I=d_1,A_x$的输出为：$$A_{x1}=M_1\cdot cosr+N_1\cdot sinr+P_1$$
  假设$A_m={\alpha }_0,I=d_2=d_1+90°,A_x$的输出为：$$A_{x2}=M_2\cdot cosr+N_2\cdot sinr+P_2$$
  然后，

  按照下面公式便可计算：
  

  磁通门计算公式与上面相似。

1.3 校准之后的效果

   采用正交法和数值拟合定标法分别计算定标系数。比较所得结果如下表。
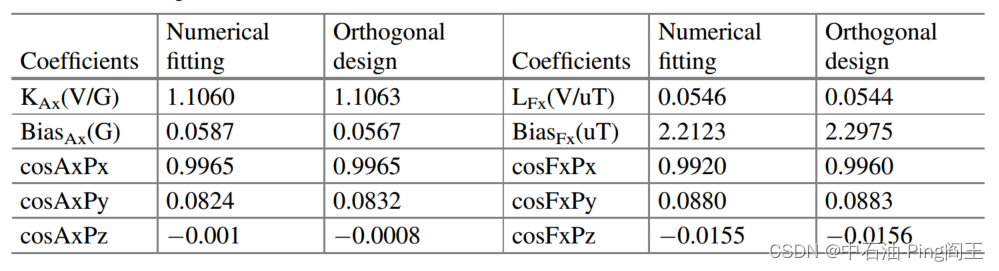
  两种定标方法在计算系数方面差异不大。利用这些系数计算井眼倾角和方位角如下图所示。

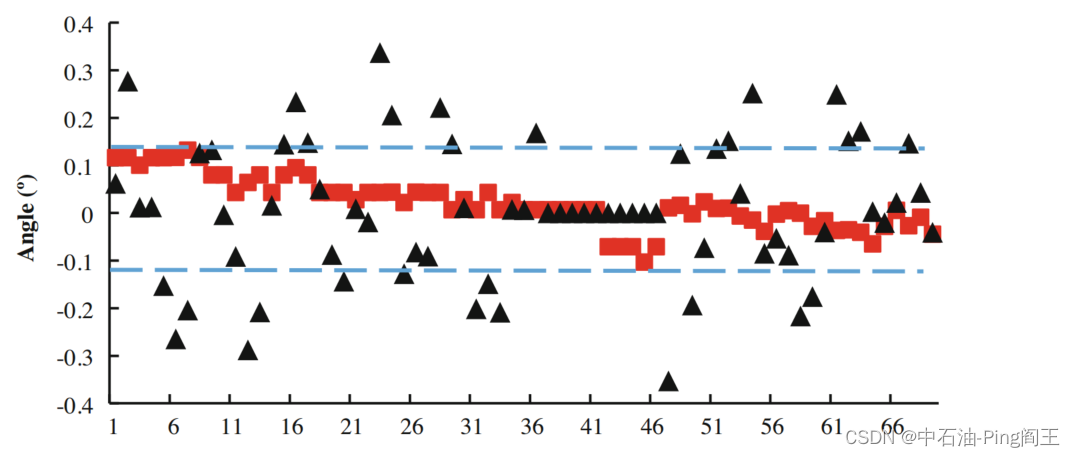
  红色代表倾角的误差，黑色代表方位角的误差r。
  1. 在旋转导向系统中，必须建立一个配备三轴磁通门和三轴加速度计的测量系统，但安装误差不可避免，必须进行校准。
  2. 建立了能很好地满足现场应用要求的标定模型。倾角和方位角的最终测量误差很小。
  3.正交法与曲线拟合法在计算标定系数上差别不大，但曲线拟合法操作简便，标定仪器结构简单，即使标定仪器的精度比以前低，也可以像正交法一样得到非常精确的计算系数，更适合工程应用。

二、往期回顾

课题学习(一)----静态测量
课题学习(二)----倾角和方位角的动态测量方法（基于磁场的测量系统）
课题学习(三)----倾角和方位角的动态测量方法（基于陀螺仪的测量系统）
课题学习(四)----四元数解法
课题学习(五)----阅读论文《抗差自适应滤波的导向钻具动态姿态测量方法》