【数据结构】二叉树--链式结构的实现 (遍历)

目录

一 二叉树的遍历

1 构建一个二叉树

2 前序遍历

3 中序遍历

4 后续遍历

5 层序 

6 二叉树销毁

二 应用(递归思想)

1 二叉树节点个数

2 叶子节点个数

3 第K层的节点个数

4 二叉树查找值为x的节点

5 判断是否是二叉树

---

一 二叉树的遍历

学习二叉树结构，最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则，依次对二叉 树中的节点进行相应的操作，并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历 是二叉树上最重要的运算之一，也是二叉树上进行其它运算的基础

二叉树是： 1. 空树  2. 非空：根节点，根节点的左子树、根节点的右子树组成的。

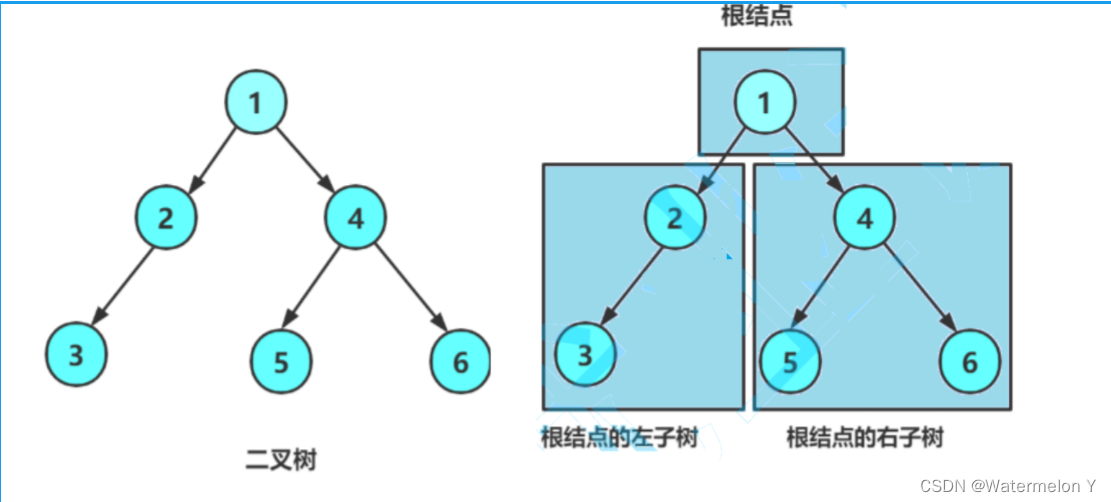
前序、中序以及后序遍历： 

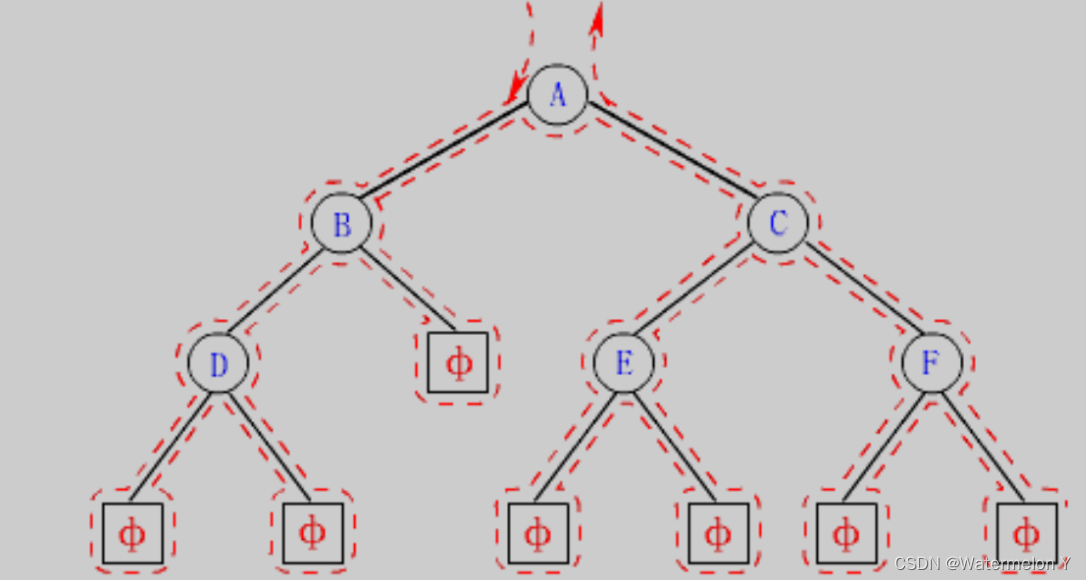
按照规则，二叉树的遍历有：前序/中序/后序的递归结构遍历：

1. 前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。

2. 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中（间）。

3. 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。

由于被访问的结点必是某子树的根，所以N(Node）、L(Left subtree）和R(Right subtree）又可解释为 根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。

代码实现:

1 构建一个二叉树

typedef struct BinaryTreeNode
{
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
	int val;
}BTNode;
 
BTNode* BuyNode(int x)
{
	BTNode* node = (BTNode*)malloc(sizeof(BTNode));
	if (node == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}
	node->left = NULL;
	node->right = NULL;
	node->val = x;
	return node;
}
 
 
 
int main()
{
	BTNode* node1 = BuyNode(1);
	BTNode* node2 = BuyNode(2);
	BTNode* node3 = BuyNode(3);
	BTNode* node4 = BuyNode(4);
	BTNode* node5 = BuyNode(5);
	BTNode* node6 = BuyNode(6);
 
	node1->left = node2;
	node1->right = node4;
	node2->left = node3;
	node4->left = node5;
	node4->right = node6;
 
 
	PrevOrder(node1);
	printf("\n");
 
	InOrder(node1);
	printf("\n");
 
	PostOrder(node1);
	printf("\n");
	return 0;
}

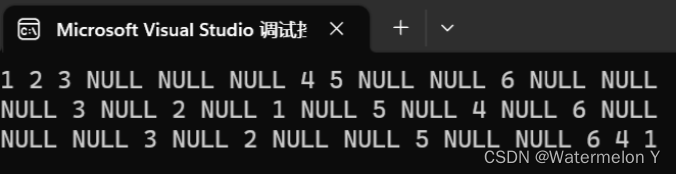
 2 前序遍历

//前序遍历
void PrevOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
 
	printf("%d ", root->val);
	PrevOrder(root->left);
	PrevOrder(root->right);
}

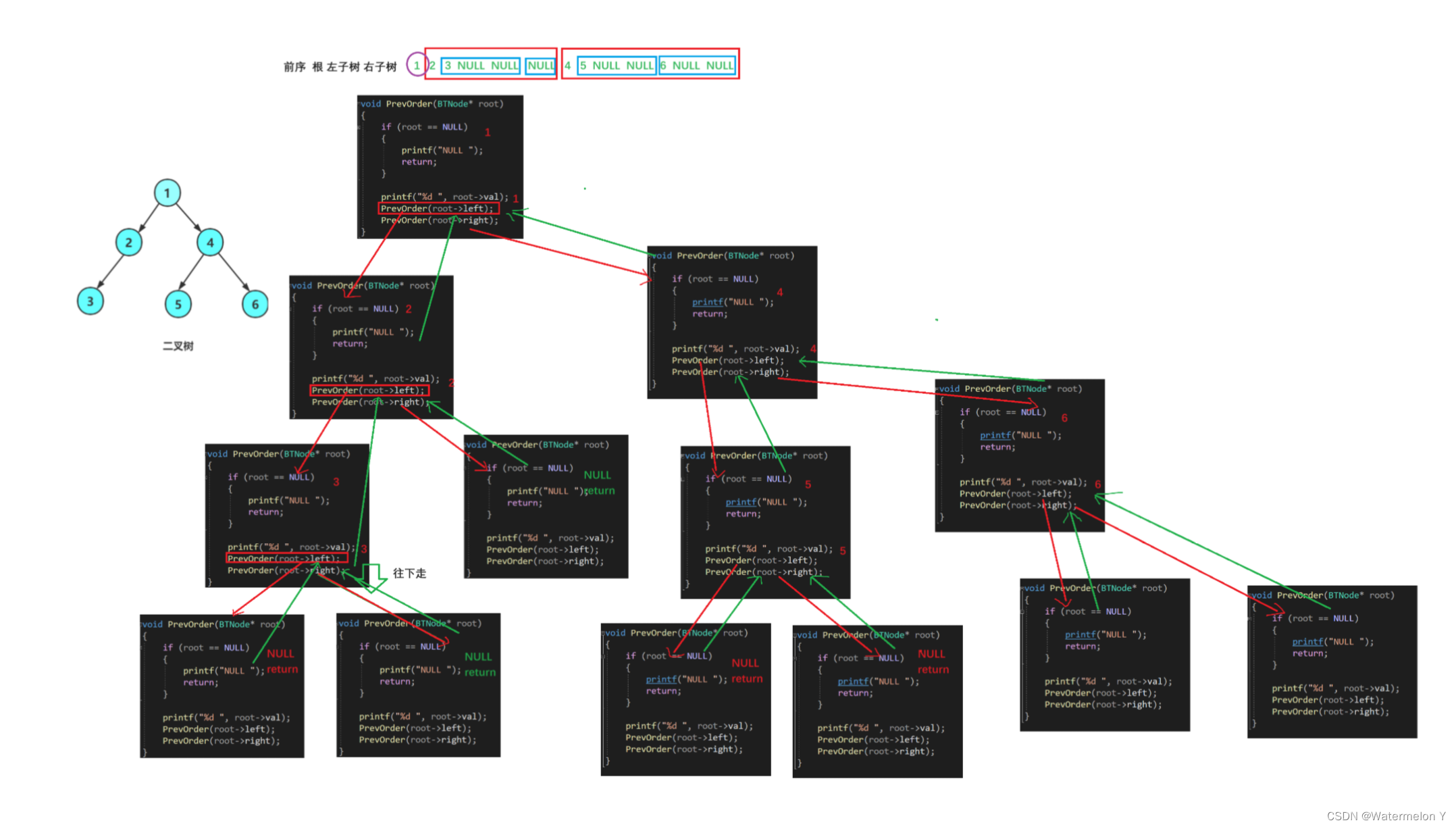
3 中序遍历

//中序遍历
void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
 
	InOrder(root->left);
	printf("%d ", root->val);
	InOrder(root->right);
}

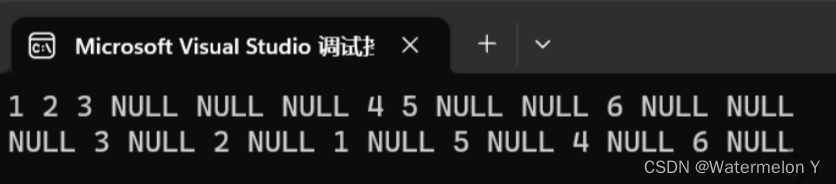
 4 后续遍历

//后序遍历
void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
 
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%d ", root->val);
}

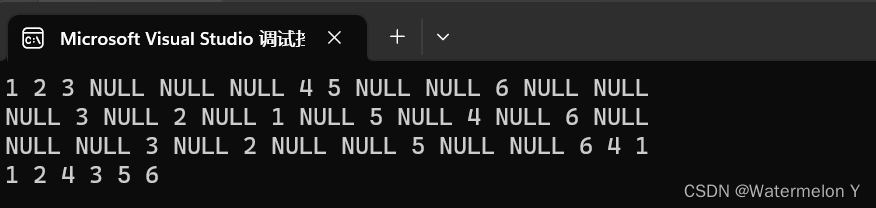
5 层序 

void QueueInit(Que* pq)
{
	assert(pq);
	pq->head = pq->tail = NULL;
	pq->size = 0;
}
 
 
void QueuePush(Que* pq, QDataType x)
{
	assert(pq);
	QNode* newnode = (QNode*)malloc(sizeof(QNode));
	if (newnode == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}
	newnode->next = NULL;
	newnode->val = x;
 
	if (pq->tail == NULL)
	{
		pq->head = pq->tail = newnode;
	}
	else
	{
		pq->tail->next = newnode;
		pq->tail = newnode;
	}
	pq->size++;
 
}
 
bool QueueEmpty(Que* pq)
{
	assert(pq);
	return pq->head == NULL;
}
 
 
void QueuePop(Que* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
	if (pq->head->next == NULL)
	{
		free(pq->head);
		pq->head = pq->tail = NULL;
	}
	else
	{
		QNode* next = pq->head->next;
		free(pq->head);
		pq->head = next;
	}
	pq->size--;
}
 
QDataType QueueFront(Que* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
 
	return pq->head->val;
}
 
void LevelOrder(BTNode* root)
{
	Que q;
	QueueInit(&q);
	if (root)
	{
		QueuePush(&q, root);
	}
 
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		printf("%d ", front->val);
		if (front->left)
		{
			QueuePush(&q, front->left);
		}
		if (front->right)
		{
			QueuePush(&q, front->right);
		}
 
		QueuePop(&q);
	}
}

6 二叉树销毁

//二叉树的销毁
void TreeDestroy(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
 
	TreeDestroy(root->left);
	TreeDestroy(root->right);
	free(root);
 
}

二 应用(递归思想)

1 二叉树节点个数

int size = 0;
int TreeSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	else
	{
		size++;
	}
	TreeSize(root->left);
	TreeSize(root->right);
	return size;
 
}

我们还可以改进

int TreeSize(BTNode* root)
{
	return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}

 2 叶子节点个数

int TreeLeafSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}
 
	return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}

3 第K层的节点个数

int TreeKLevel(BTNode* root, int k)
{
	assert(k > 0);
	if (root == NULL)
	{
		return 0;
	}
	if (k == 1)
	{
		return 1;
	}
 
	return TreeKLevel(root->left, k-1) + TreeKLevel(root->right, k-1);
}

 4 二叉树查找值为x的节点

BTNode* TreeFind(BTNode* root, int x)
{
	if (root == NULL)
	{
		return NULL;
	}
 
	if (root->val == x)
	{
		return root;
	}
 
	BTNode* ret = NULL;
	//从左树找 找到了就返回 不找右树了
	ret = TreeFind(root->left, x);
	if (ret)
	{
		return ret;
	}
 
	//左树没找到 就开始找右树
	ret = TreeFind(root->right, x);
	if (ret)
	{
		return ret;
	}
	
}

5 判断是否是二叉树

void QueueInit(Que* pq)
{
	assert(pq);
	pq->head = pq->tail = NULL;
	pq->size = 0;
}
 
void QueueDestroy(Que* pq)
{
	assert(pq);
	QNode* cur = pq->head;
	while (cur)
	{
		QNode* next = cur->next;
		free(cur);
		cur = next;
	}
	pq->head = pq->tail = NULL;
	pq->size = 0;
}
 
void QueuePush(Que* pq, QDataType x)
{
	assert(pq);
	QNode* newnode = (QNode*)malloc(sizeof(QNode));
	if (newnode == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}
	newnode->next = NULL;
	newnode->val = x;
 
	if (pq->tail == NULL)
	{
		pq->head = pq->tail = newnode;
	}
	else
	{
		pq->tail->next = newnode;
		pq->tail = newnode;
	}
	pq->size++;
 
}
 
bool QueueEmpty(Que* pq)
{
	assert(pq);
	return pq->head == NULL;
}
 
 
void QueuePop(Que* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
	if (pq->head->next == NULL)
	{
		free(pq->head);
		pq->head = pq->tail = NULL;
	}
	else
	{
		QNode* next = pq->head->next;
		free(pq->head);
		pq->head = next;
	}
	pq->size--;
}
 
QDataType QueueFront(Que* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
 
	return pq->head->val;
}
 
int TreeComplete(BTNode* root)
{
	Que q;
	QueInit(&q);
	if (root != NULL)
	{
		QueuePush(&q, root);
	}
 
	//找空节点
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		if (front == NULL)
		{
			break;
		}
		QueuePush(&q, front->left);
		QueuePush(&q, front->right);
		QueuePop(&q);
	}
 
	//已经找到空节点
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		if (front != NULL)
		{
			QueueDestroy(&q);
			return false;
		}
	}
 
	QueueDestroy(&q);
	return true;
}

二叉树的链式结构的本质思想是递归, 对于递归不了解的小伙伴可以看看我之前的博客, 也可以自己尝试画一下递归展开图,下一节讲OJ题目.实战才最有效!继续加油!