【例题】逆波兰表达式求值(图解+代码)

【例题】逆波兰表达式求值(图解+代码)

题目描述 :

逆波兰表示法是一种将运算符（operator）写在操作数（operand）后面的描述程序（算式）的方法。举个例子，我们平常用中缀表示法描述的算式（1 + 2）*（5 + 4），改为逆波兰表示法之后则是1 2 + 5 4 + *。相较于中缀表示法，逆波兰表示法的优势在于不需要括号。

请输出以逆波兰表示法输入的算式的计算结果。

输入格式:

在一行中输入1个算式。相邻的符号（操作数或运算符）用1个空格隔开。

输出格式:

在一行中输出计算结果。

限制:

2≤算式中操作数的总数≤100

1≤算式中运算符的总数≤99

运算符仅包括“+”、“-”、“*”，操作数、计算过程中的值以及最终的计算结果均在int范围内。

样例 :

输入样例1:

4 3 + 2 -
1

输出样例1:

5
1

输入样例2:

1 2 + 3 4 - *
1

输出样例2:

-3
1

逆波兰表达式

解释

逆波兰表达式是数学表达式,表现为操作符在操作数的后面,又称 后缀表达式,后序表达式. 相对的 应该还有波兰表达式,波兰表达式就是操作符在操作数的前面,又称 前缀表达式.

如果操作符的元数（arity）是固定的，则语法上不需要括号仍然能被无歧义地解析。不需要括号来标识操作符的优先级。

---

优点

逆波兰表达式是无括号的表达式,那么 逆波兰表达式 的运算就不像 中缀表达式 那样,会因为括号的位置改变表达式运算的优先级 ,这就是逆波兰表达式的优点 : 运算无歧义.

例如 : 
前缀表达式 1+2*3 和 (1+2)*3 因为括号的添加表示两种中缀表达式
后缀表达式则可无歧义的将其分别表示为1 2 3 * + 和 1 2 + 3 *
1
2
3

---

转换

这个题目涉及到的是后缀表达式,我们这里讲 中缀表达式和后缀表达式的相互转换,也就是知道其中一个表达式,然后求另一个表达式.

已知 中缀表达式 求 后缀表达式

eg : 中缀表达式 1+2-3*4+5

• 步骤

1. 按照中缀表达式的计算优先级,对中缀表达式的所有计算步骤添加括号

2. 从左至右遍历一旦遇到括号就将当前等级的操作符移到括号的后面,继续遍历

3. 直到将所有括号中的符号全部移到括号的后面

备注: 已知 中缀表达式 求 前缀表达式 是同样的方式 添加括号,移动括号,只是此时把 操作符 移动操括号的前面.

---

计算

给定一个 后缀表达式 去计算表达式的结果. 由于无论是前缀 ,中缀 还是后缀 全部都是一个可以计算的表达式 , 那么通过中缀表达式转换成的前缀/后缀表达式 计算的结果一定和中缀表达式计算出来的结果相同.

• 步骤

利用栈数据结构 用来存储操作数,首先 遍历 后缀表达式 ,遇见 操作数 则入栈, 遇见 操作符 则从栈中弹出两个 操作数,先弹出的作为 右操作数,后弹出的作为 左操作数 ,并进行计算,将计算结果 入栈,继续遍历,直到后缀表达式遍历结束,此时栈中剩下一个操作数,即为 后缀表达式的结果.

---

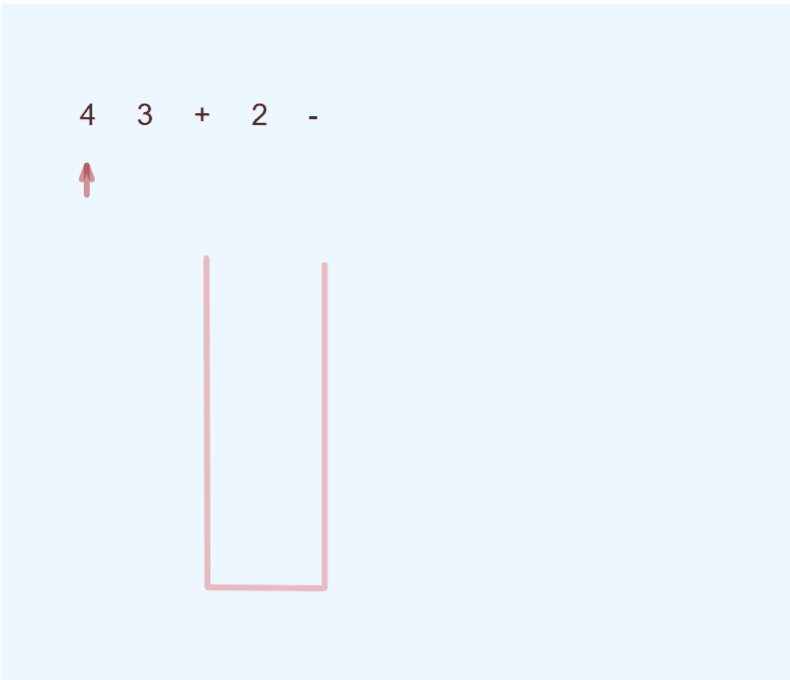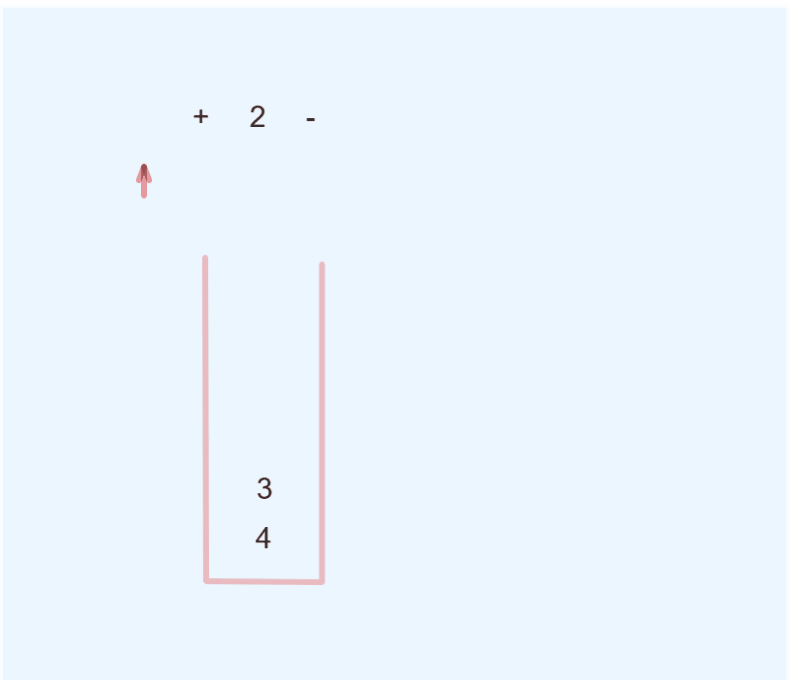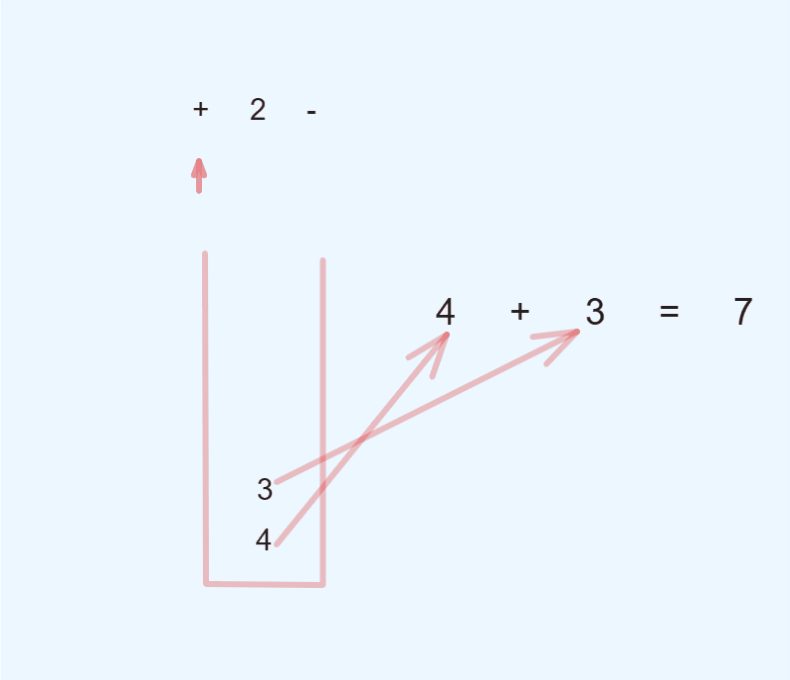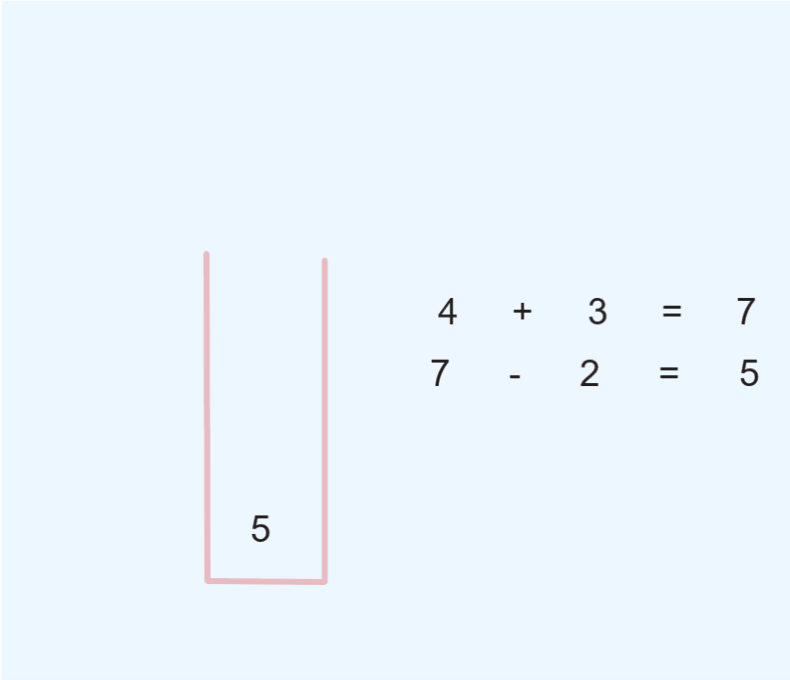
代码

package day02;

import java.util.Scanner;
import java.util.Stack;

public class ReversePolishExpression {
    public static void main(String[] args) {
        //创建一个栈,用来存储 操作数
        Stack<Integer> stack = new Stack<>();
        Scanner scan = new Scanner(System.in);

        String input = scan.nextLine();
        String[] tokens = input.split(" ");
        int answer;

        for (String token : tokens) {
            if (token.equals("+") || token.equals("-") || token.equals("*")) {
                if (stack.size() < 2) {
                    System.out.println("输入的逆波兰表达式不合法！");
                    return;
                }
                int cr = stack.pop();
                int cl = stack.pop();

                switch (token) {
                    case "+":
                        answer = cl + cr;
                        break;
                    case "-":
                        answer = cl - cr;
                        break;
                    case "*":
                        answer = cl * cr;
                        break;
                    default:
                        answer = 0;  // 处理未知运算符的情况
                        break;
                }
                stack.push(answer);
            } else {
                try {
                    int num = Integer.parseInt(token);
                    stack.push(num);
                } catch (NumberFormatException e) {
                    System.out.println("输入包含无效的操作数: " + token);
                    return;
                }
            }
        }
            if (stack.size() == 1) {
                System.out.println(stack.pop());
            } else {
                System.out.println("输入的逆波兰表达式不合法！");
            }
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57