【深蓝学院】手写VIO第7章--VINS初始化和VIO系统--笔记

0. 内容

1. VIO回顾

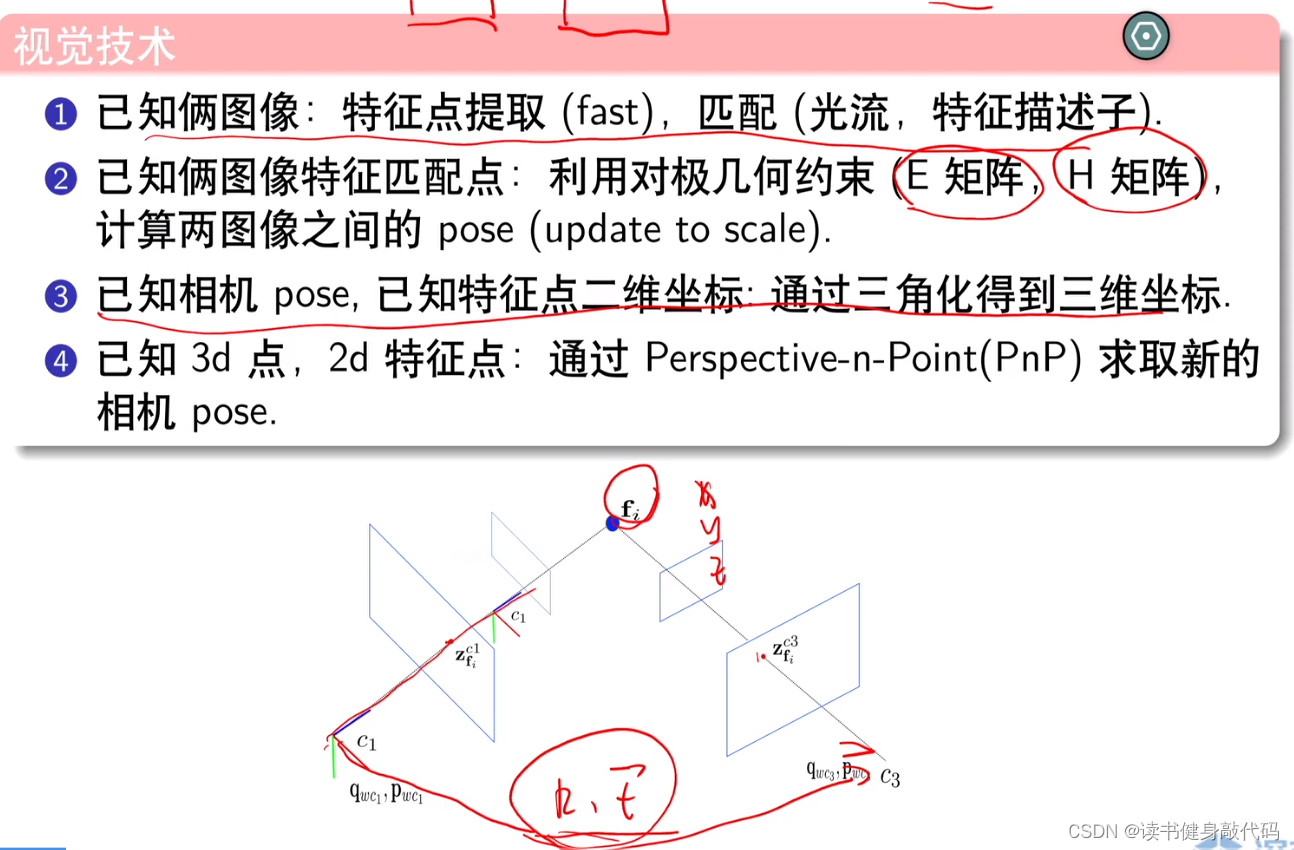
整个视觉前端pipeline回顾：

1. 两帧图像，可提取特征点，特征匹配（描述子暴力匹配或者光流）
2. 已知特征点匹配关系，利用几何约束计算relative pose([R|t])，translation只有方向，没有尺度
3. 使用三角化获得3维坐标，即可完成vslam系统的初始化
4. 有了3D特征点，后续可根据特征跟踪，使用PnP求解Camera Pose，无需再使用几何约束(求解$argmin\frac{1}{2}||u_i-\frac{1}{s}KT{P}_i|{|}_2^2$)

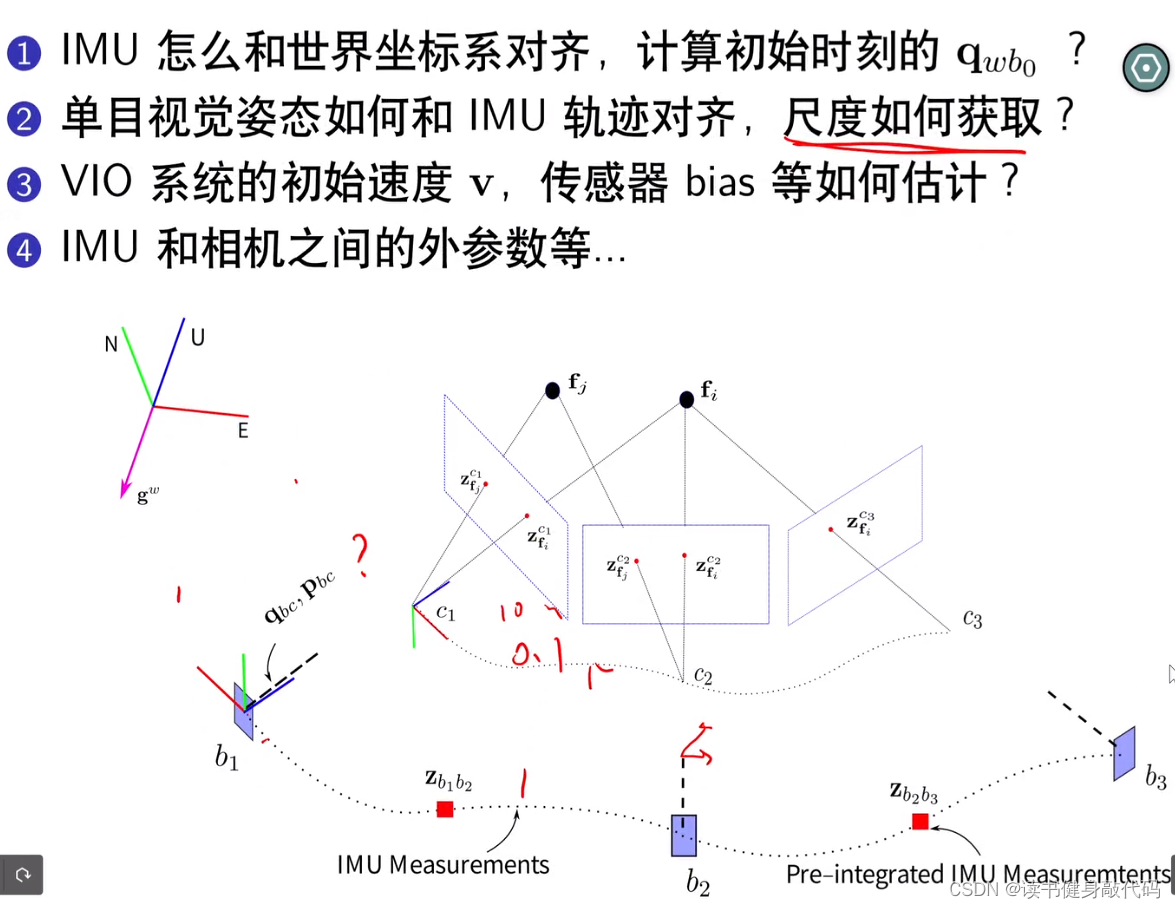
1. IMU的加速度要和世界系的重力进行对齐
   
   世界系重力假设(0，0，-9.81)，IMU第一帧估计出一个${}^{c}g{=}^c{R}_{cb}{g}_b$，就可以求出第一帧camera在world下的pose（带头大哥）

2. 视觉的尺度和IMU尺度要进行对齐

3. VIO系统速度，传感器bias需要估计

4. IMU和相机的外参Tic

知道了z轴的法向量就能估计roll和pitch(tilt)，但是yaw不可观。

2. VINS鲁棒初始化

2.1 pipeline overview

以下所有思想基本都来源于VINS-MONO

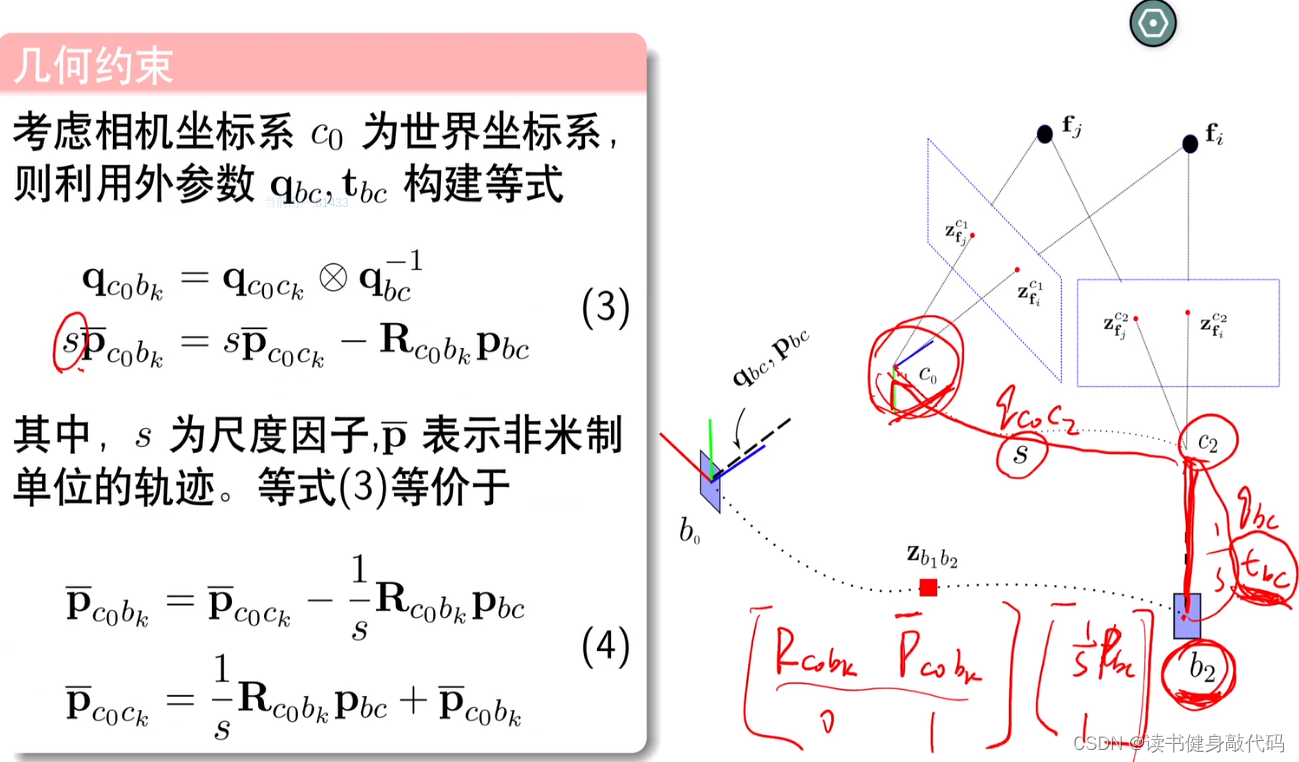
式(3)第一行是旋转约束，第二行是平移约束。

---

更新式(3)的推导方式

---

IMU积分是米制单位，但是camera不是，camera存在一个缩放因子，标定出外参$[R_{bc},t_{bc}]$之后，可以求得尺度因子s，先对坐标系，R,t的数学表示做一下说明：
旋转脚标相连时相消，刚性连接在不同时刻的的观测相同，平移左上角是观测系，右下角从左到右；平移乘旋转后平移向量不变，但观测系改变。

式(4)第一行这样理解：
$${}^{c_0}{\overline{p}}_{c_0{b}_k}={}^{c_0}{\overline{p}}_{c_0{c}_k}-\frac{1}{s}{}^{c_0}{R}_{c_0{b}_k}{}^b{p}_{bc}(2.1)$$
左上角都是观测系，即在什么系下看这个量，由于刚性连接在不同观测系，不同时间下相同，且平移乘旋转后旋转向量不变，但观测系改变，所以$${}^b{p}_{bc}={}^{b_k}{p}_{b_k{c}_k}(2.2)$$
所以将(2.2)带入式(2.1)可得：
$${}^{c_0}{\overline{p}}_{c_0{b}_k}={}^{c_0}{\overline{p}}_{c_0{c}_k}-{}^{c_0}{\overline{p}}_{b_k{c}_k}={}^{c_0}{\overline{p}}_{c_0{c}_k}+{}^{c_0}{\overline{p}}_{c_k{b}_k}(2.3)$$
即在$c_0$系下进行将${}^{c_0}{\overline{p}}_{c_0{c}_k}+{}^{c_0}{\overline{p}}_{c_k{b}_k}$向量相加，物理意义：在$c_0$系下看$b_k$，等于$c_0,c_k$的外参+camera和IMU外参转到$c_0$系下，去掉尺度。
标定出Camera和IMU外参之后，利用式(2.1)就可以求出尺度因子。

下面以VINS-MONO为例进行讨论：

Tbc外参的Rotation很重要，而Translation由于可能离得比较近，所以相对来说没有Rotation重要

2.2 外参估计

旋转约束：两种路径求取的$q_{c_k{b}_{k+1}}$应该相同。

这里的未知量只有外参$q_{bc}$，也可以简单地理解为一段时间内，camera出一段pose(trajectory)，imu积分出一段pose(trajectory)，这两段pose理想情况下只有外参的差异，（不考虑$t_{bc}$的情况下）可以将这两段pose align起来，残差是两段pose align的残差，待估计量就是外参，做LSP的结果就是外参。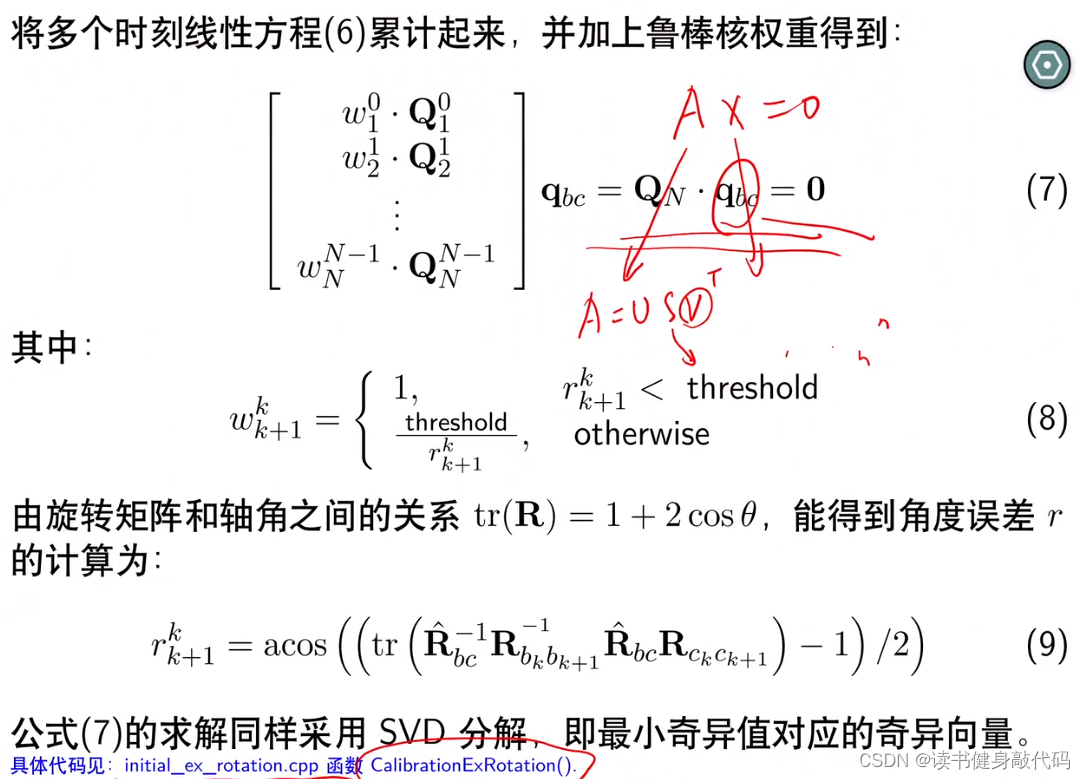

VINS论文中将多个时刻的数据累计起来，并使用了鲁棒核函数对每一项进行了加权，权值计算方法：有$tr(R)=1+2cos\theta$（可以看wiki），式(9)目的就是为了计算鲁棒核函数的权值，用角度误差和阈值来计算每个观测在整个问题中的权值，中的那一大块矩阵就是式（5）把左边移到右边而得，因为求的是相同的量（如$q_{b_k{c}_{k+1}}$），所以理想情况下连乘应该是Identity，但实际上，如果外参估的不准，这个角度会较大（>threshold），所以式（8）将大于threshold的部分的权值设的较小，进行了抑制。

最终对$q_{bc}$的求解还是对式(7)使用SVD分解，取$V^T$最后一列作为解。

(参考这篇博客参考这篇博客中使用Lanrange算子证明取$V^T$最后一列是我们所求的解。)

论文中还对SVD分解的倒数第二小奇异值进行了判断，如果小于阈值则认为该次估计无效，重新采集数据进行估计。（这和增多数据或者降低数据噪声来提升数据信噪比是一样的目的，都是为了提高数值稳定性）

2.3 gyro bias估计

进行gyro bias估计的原因是如果不估计，那么gyro进行积分会有误差，导致预积分误差大，影响系统工作。
思路：将bias作为待估参数，构建残差转化为LSP求解。而LSP残差的构建一般是用对同一量物理量的预测和观测相减，带着这个思想看下面的讨论会更易理解。

误差构建图示，即通过能算出来的$q_{c_0{b}_k}$和$q_{c_0{b}_{k+1}}$算出$q_{b_k{b}_{k+1}}$的预测，然后与测量作差即得residual：

式(10)就是将$b_k$到$b_{k+1}$时刻之间imu的rotation都转到$c_0$系下进行align：

• 前两项四元数相乘代表求在$c_0$系下看imu在$b_k$到$b_{k+1}$时刻之间的relative rotation
• 第3项$q_{b_k{b}_{k+1}}$是IMU积分而来的两时刻间的relative rotation真值（会受到gyro bias的影响），对其进行一阶Taylor展开，带入(10)，假设${\hat{q}}_{b_k{b}_{k+1}}$测量的比较准，那么与前面的估计值相乘得Identity，剩下的矩阵里面的就是residual ${\theta }_{err}$，求Jacobian构建正定方程，求解gyro bias（这里bias不知道为什么为0，又说不一定为0，因为测量不一定准确，先挖个坑，看代码了再说）

这跟前面估计外参的是一样的，都是使用的旋转约束。
至此，已经能够估计出

• IMU和camera的外参（仅$R_{bc}$）
• gyro bias

2.4 初始化速度，重力，尺度因子

预积分量的公式回顾3.1节
与world有关的量都是不可观的，所以我们就令与world有关的量都锚定在$c_0$帧，而IMU使得roll和pitch可观，所以$q_{b_{i}w}$是可观的，我们要进行估计。

式(15)带入推导

式(16)矩阵侧都是测量量，包括IMU积分和外参，右侧是待估计变量加一些高斯白噪声

式(17)(18)推导补充

假设z的噪声服从高斯分布，则其观测也服从高斯分布，(16)即为对z的预测，结合观测即可构建最小二乘问题LSP，使用L-M等方法进行求解（LSP问题就是如此构建的，有观测，想办法构建出这个观测的预测量，并从中抽离出待估计变量，就转化为LSP问题）。

小结一下：

• 通过旋转约束可以估计Tbc外参，imu bias；
• 通过平移约束可以估计重力向量，速度和尺度(都在大X变量中)。

2.5 讨论

讨论：上述优化过程中没有加入对于重力向量模长的约束，可能导致优化之后的重力向量模长不为9.81左右，所以需要加入。
课上提到李代数那边好像也有种重力向量参数化的方法，可能叫TSE(3)之类的。

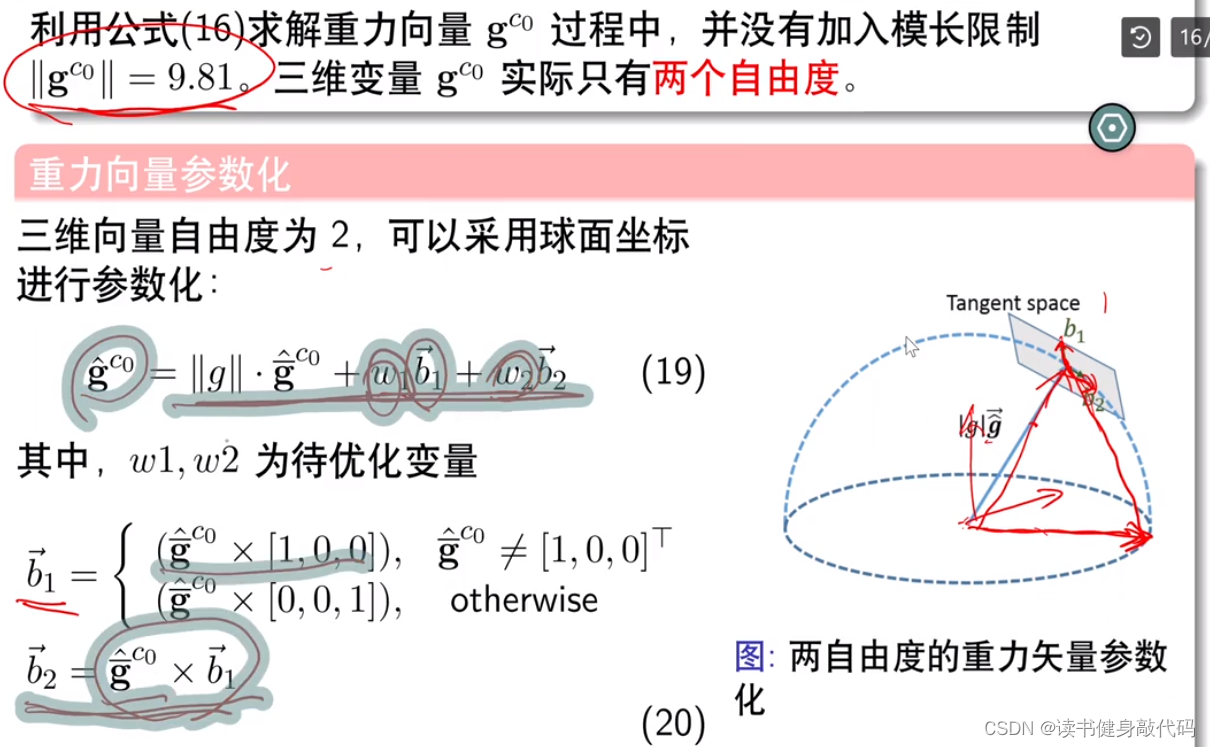
上面的优化问题没有加入重力模长为9.81的这个约束，为了加入这个约束，引入一种对重力向量参数化的方式，分别构造出与重力向量垂直的两个基向量$b_1,b_2$，通过最小化这两个基向量的参数${\omega }_1,{\omega }_2$来使得重力向量的估计${\hat{g}}^{c_0}$更准确。

优化后的重力向量结果当做初始值，与$[1,0,0]$或者$[0,0,1]$叉乘得一个基向量$b_1$，再和$b_1$叉乘得$b_2$，用这两个基向量和优化结果来参数化重力向量，参数为${\omega }_1,{\omega }_2$。

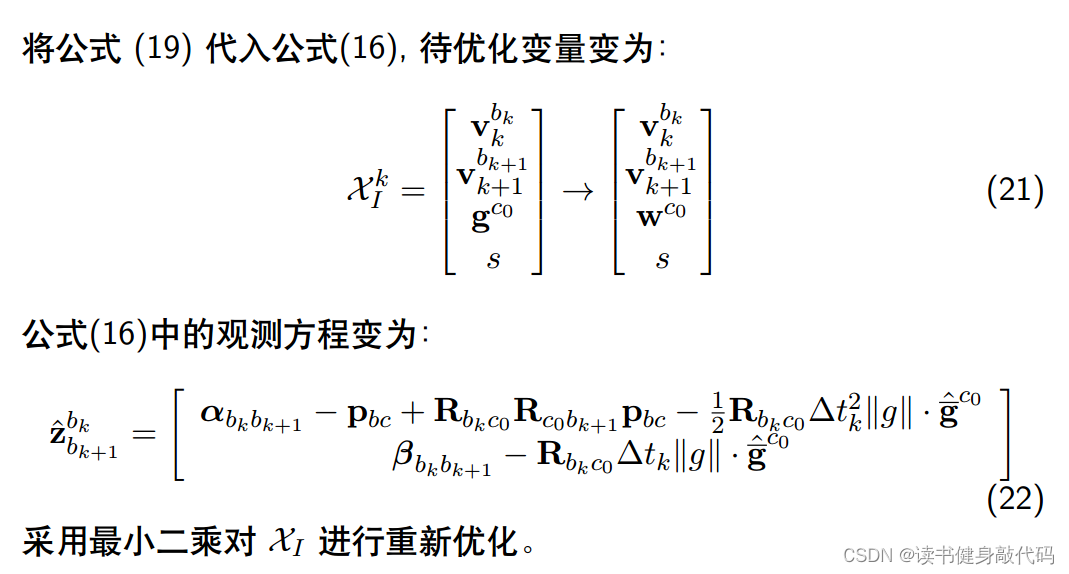
将约束加入到优化问题中，这个到时候看代码吧。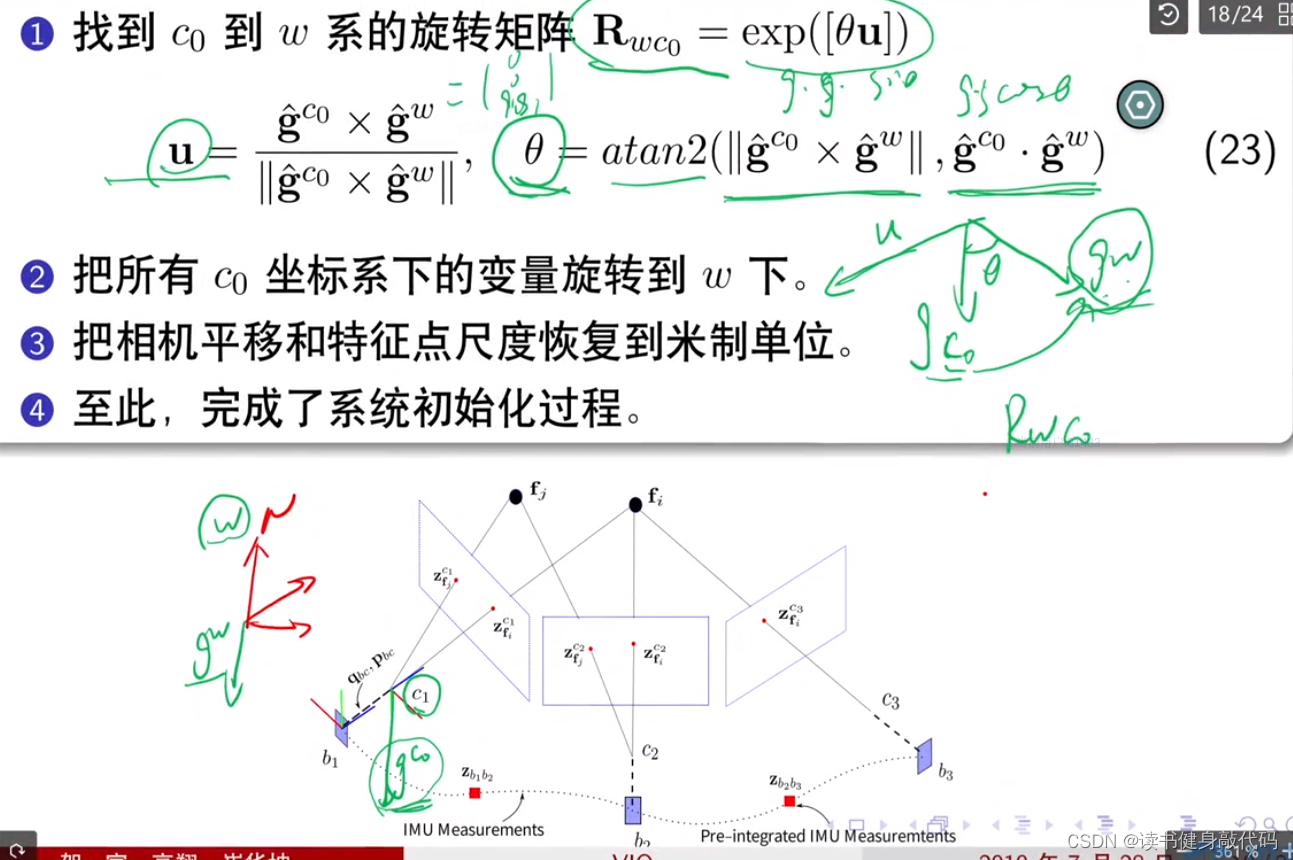

估计出在$c_0$系下的重力向量之后，结合重力向量的GT，使用式(23)可求出第1帧$c_0$到world系下的rotation，包括一个旋转轴和一个旋转角。

2.6 疑问

1. $g^{c_0}$不准，所以估出来的$R_{w{c}_0}$也不准，后面用$R_{w{c}_0}$算出来的$R_{w{c}_1}$，$R_{w{c}_2}...$也不准啊。
   答：因为$R_{w{c}_1}$，$R_{w{c}_2}...$会被加入到BA中进行优化这些不准会导致重投影误差，预积分等不准，在优化过程中会不断调整这些pose使它们更准，但是估计了$R_{w{c}_0}$后会使pose跟world系产生关联，所以还是有必要的。

2. 没估计加计bias：加计bias非常小，可能是1e-4这种量级的，相对于重力9.81，就淹没了，可能估计不出来，且影响也不大，在qintong的论文中有说明。
3. 没估平移外参p_{bc}，因为可能只有几厘米，很小，且相对于Rotation来说，Translation是一个线性的变换，不会使得系统变得非常复杂。

静止初始化，静止时初速度为0，加计测出来的直接就是重力，gyro的bias可以取一段时间的数据平均，作为bias。

这里给出的两篇参考文献里面有自己的初始化方法，
a. 是camera出的pose插值计算出来角速度和imu测量的应该相同，二者构建出来残差进行优化
b. 使用了紧耦合的方法，IMU和camera各出一段pose，然后align，进行init

看过论文之后，再来刷一遍视频吧。

3. VINS系统

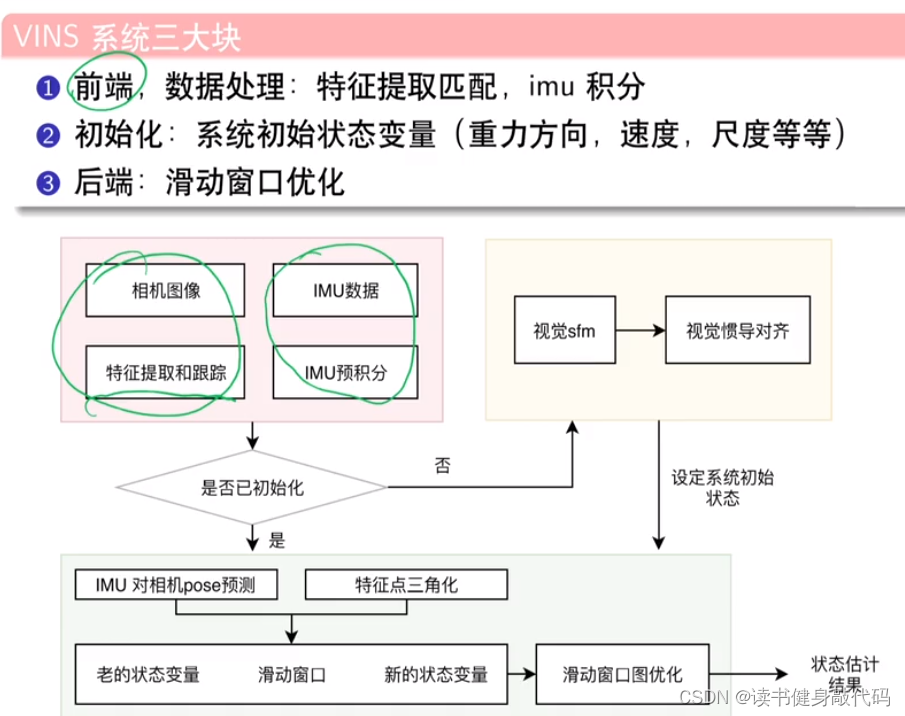
整个VINS系统的cost function，分为3大部分，关系图模型也如下所示：

4. 代码讲解

作业代码主要基于VINS-MONO开发，如果不关注系统的初始化的话，整个后端的求解还是较简单的，把之前3456的串起来就差不多了。开作业。

5. 待读文献

1.

1Zhenfei Yang and Shaojie Shen. “Monocular visual–inertial state estimation with online initialization and camera–IMU extrinsic calibration”. In: IEEE Transactions on Automation Science and Engineering 14.1 (2016), pp. 39–51.

2.

Tong Qin and Shaojie Shen. “Robust initialization of monocular visual-inertial estimation on aerial robots”. In: 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). IEEE. 2017, pp. 4225–4232.

3.

Janne Mustaniemi et al. “Inertial-based scale estimation for structure from motion on mobile devices”. In: 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). IEEE. 2017, pp. 4394–4401.

4.

Javier Domínguez-Conti et al. “Visual-Inertial SLAM Initialization: A General Linear Formulation and a Gravity-Observing Non-Linear Optimization”. In: 2018 IEEE International Symposium on Mixed and Augmented Reality (ISMAR). IEEE. 2018, pp. 37–45.

5.