二叉树的最近公共祖先

🎈个人主页:🎈 :✨✨✨初阶牛✨✨✨
🐻强烈推荐优质专栏: 🍔🍟🌯C++的世界(持续更新中)
🐻推荐专栏1: 🍔🍟🌯C语言初阶
🐻推荐专栏2: 🍔🍟🌯C语言进阶
🔑个人信条: 🌵知行合一
🍉本篇简介:>:记录力扣题 二叉树的最近公共祖先.
金句分享:
✨生活本就沉默,但是跑起来有风!✨

前言

题目来源于:力扣
题目链接:传送门

题目介绍:

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

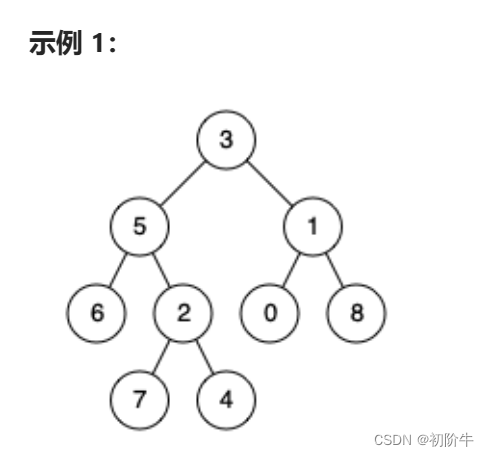
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3

解释：节点 5 和节点 1 的最近公共祖先是节点 3 。

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出：5

解释：节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。

解题思路

幻想:
如果该树是三叉树就好了,有一个指向父亲的指针,那样就可以转化为两个链表相交,求交点,只需要快慢指针就行了.

正经解题:

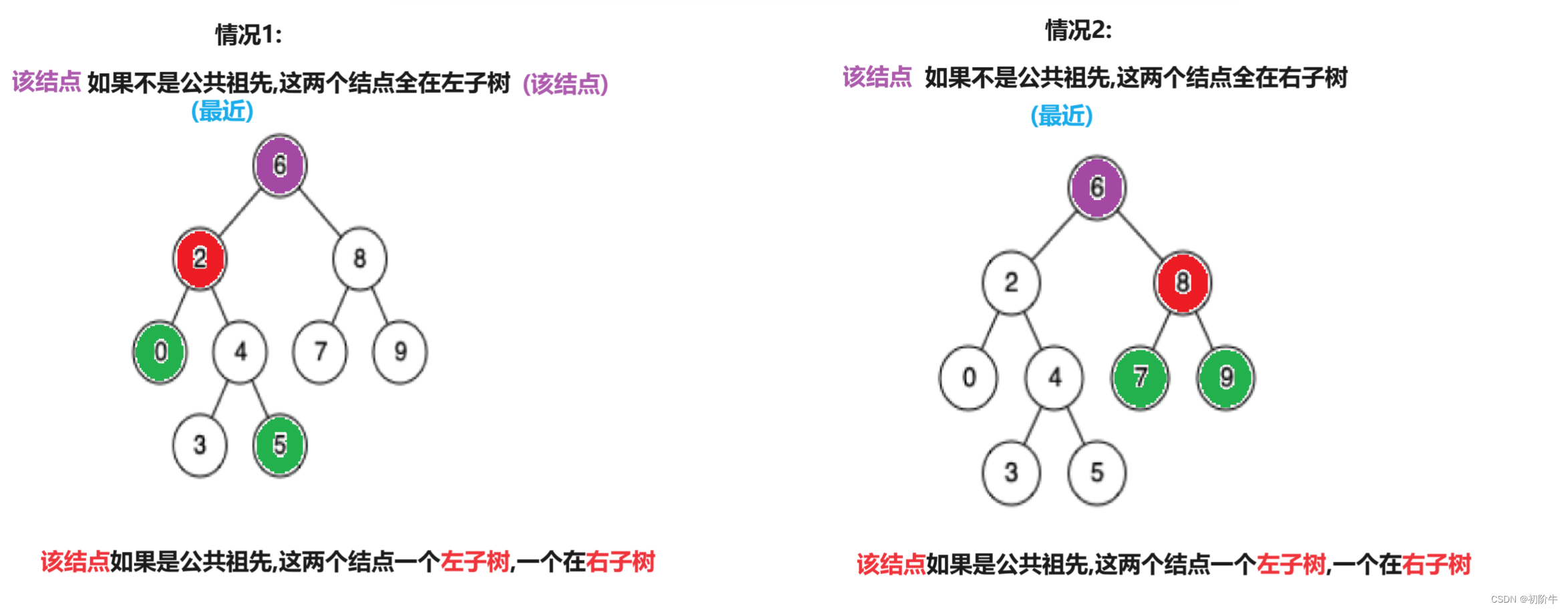
1. 试着观察最近公共祖先,如果只是普通的祖先,则这两个结点都在其中的一个子树中.
   (1)全在该结点的左子树 (2)全在该结点的右子树
2. 如果是最近的公共祖先,则一个结点在左子树,一个在右子树.
3. (1) 如果全在左子树,则往左子树方向继续找.
   (2) 如果全在右子树,同理;
4. 特殊情况,其中一个是另一个的祖先(父亲),直接返回该结点(祖先)即可.

代码实现:

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(root==p||root==q)	//其中一个是另一个的祖先
        {
            return root;
        }
        
        //判断在不在左子树
        bool left_p=find(root->left,p);
        bool left_q=find(root->left,q);
		
		//判断在不在右子树
        bool right_p=!left_p;
        bool right_q=!left_q;
	
		
        if(left_p && left_q)
        {
        	//如果全在左子树,则往左子树继续遍历
            root=lowestCommonAncestor( root->left,p,q);
        }
        else if(right_p && right_q)
        {
        	//如果全在右子树,则往右子树继续遍历
            root=lowestCommonAncestor( root->right,p,q);
        }
        return root;
    }
    bool find(TreeNode* root,TreeNode* node)
    {
        if(root==nullptr) return false;
        if(root==node)
        {
            return true;
        }
        return find(root->left,node)||find(root->right,node);
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39