关于SSA算法中矩阵的3种运算：转置、求逆、相乘

1、矩阵转置

  // 矩阵转置(二维矩阵)
    public static double[][] transposeTwo(double[][] matrix) {
        int rows = matrix.length;
        int cols = matrix[0].length;
        double[][] transposedMatrix = new double[cols][rows];

        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < cols; j++) {
                transposedMatrix[j][i] = matrix[i][j];
            }
        }

        return transposedMatrix;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14

矩阵转置测试：

package test;

public class transposeOne {

    // 矩阵转置(二维矩阵)
    public static double[][] transposeTwo(double[][] matrix) {
        int rows = matrix.length;
        int cols = matrix[0].length;
        double[][] transposedMatrix = new double[cols][rows];

        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < cols; j++) {
                transposedMatrix[j][i] = matrix[i][j];
            }
        }

        return transposedMatrix;
    }

    public static void printArray(double[][] array) {
        for (int i = 0; i < array.length; i++) {
            for (int j = 0; j < array[i].length; j++) {
                System.out.print(array[i][j] + " ");
            }
            System.out.println();
        }
    }

    public static void main(String[] args) {
        // 定义一个3x3的矩阵
        double[][] matrixData1= {
                {1, 2, 3},
                {0, 1, 4},
                {5, 6, 0}
        };

        double[][] f=transposeTwo(matrixData1);
        printArray(f);

    }

}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

在这里插入图片描述

2、矩阵求逆

    // 矩阵求逆（使用高斯-若尔当消元法）
    public static double[][] matrixInverse(double[][] matrix) {
        int n = matrix.length;
        double[][] result = new double[n][n];
        double[][] temp = new double[n][n];

        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                temp[i][j] = matrix[i][j];
            }
        }

        for (int i = 0; i < n; i++) {
            result[i][i] = 1;
        }

        for (int i = 0; i < n; i++) {
            double diagonalElement = temp[i][i];
            if (diagonalElement == 0) {
                throw new IllegalArgumentException("Matrix is not invertible");
            }

            for (int j = 0; j < n; j++) {
                temp[i][j] /= diagonalElement;
                result[i][j] /= diagonalElement;
            }

            for (int k = 0; k < n; k++) {
                if (k != i) {
                    double tempValue = temp[k][i];
                    for (int j = 0; j < n; j++) {
                        temp[k][j] -= tempValue * temp[i][j];
                        result[k][j] -= tempValue * result[i][j];
                    }
                }
            }
        }

        return result;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

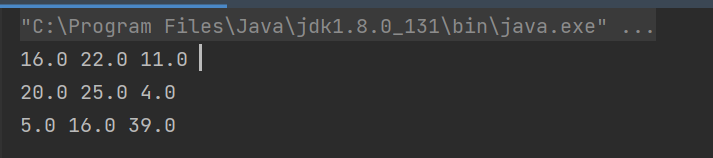
矩阵求逆测试

package test;

/**
 * 求二维矩阵的逆矩阵
 */
public class test1 {

    public static double[][] invert(double[][] matrix) {
        int n = matrix.length;
        double[][] result = new double[n][n];
        double[][] temp = new double[n][n];

        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                temp[i][j] = matrix[i][j];
            }
        }

        for (int i = 0; i < n; i++) {
            result[i][i] = 1;
        }

        for (int i = 0; i < n; i++) {
            double diagonalElement = temp[i][i];
            if (diagonalElement == 0) {
                throw new IllegalArgumentException("Matrix is not invertible");
            }

            for (int j = 0; j < n; j++) {
                temp[i][j] /= diagonalElement;
                result[i][j] /= diagonalElement;
            }

            for (int k = 0; k < n; k++) {
                if (k != i) {
                    double tempValue = temp[k][i];
                    for (int j = 0; j < n; j++) {
                        temp[k][j] -= tempValue * temp[i][j];
                        result[k][j] -= tempValue * result[i][j];
                    }
                }
            }
        }

        return result;
    }

    public static void printArray(double[][] array) {
        for (int i = 0; i < array.length; i++) {
            for (int j = 0; j < array[i].length; j++) {
                System.out.print(array[i][j] + " ");
            }
            System.out.println();
        }
    }

    public static void main(String[] args) {
        // 定义一个3x3的矩阵
        double[][] matrixData = {
                {1, 2, 3},
                {0, 1, 4},
                {5, 6, 0}
        };

        // 求矩阵的逆
        double[][] result = invert(matrixData);
        printArray(result);

    }
    
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72

在这里插入图片描述

3、矩阵相乘

   // 矩阵相乘
    public static double[][] matrixMultiply(double[][] matrix1, double[][] matrix2) {
        int rows1 = matrix1.length;
        int cols1 = matrix1[0].length;
        int rows2 = matrix2.length;
        int cols2 = matrix2[0].length;

        if (cols1 != rows2) {
            throw new IllegalArgumentException("矩阵1的列数必须等于矩阵2的行数");
        }

        double[][] result = new double[rows1][cols2];

        for (int i = 0; i < rows1; i++) {
            for (int j = 0; j < cols2; j++) {
                for (int k = 0; k < cols1; k++) {
                    result[i][j] += matrix1[i][k] * matrix2[k][j];
                }
            }
        }

        return result;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

矩阵相乘测试：

package test;

public class test_matrixMultiply {
    // 矩阵相乘
    public static double[][] matrixMultiply(double[][] matrix1, double[][] matrix2) {
        int rows1 = matrix1.length;
        int cols1 = matrix1[0].length;
        
        int rows2 = matrix2.length;
        int cols2 = matrix2[0].length;

        if (cols1 != rows2) {
            throw new IllegalArgumentException("矩阵1的列数必须等于矩阵2的行数");
        }

        double[][] result = new double[rows1][cols2];

        for (int i = 0; i < rows1; i++) {
            for (int j = 0; j < cols2; j++) {
                for (int k = 0; k < cols1; k++) {
                    result[i][j] += matrix1[i][k] * matrix2[k][j];
                }
            }
        }

        return result;
    }

    public static void printArray(double[][] array) {
        for (int i = 0; i < array.length; i++) {
            for (int j = 0; j < array[i].length; j++) {
                System.out.print(array[i][j] + " ");
            }
            System.out.println();
        }
    }

    public static void main(String[] args) {
        // 定义一个3x3的矩阵
        double[][] matrixData1= {
                {1, 2, 3},
                {0, 1, 4},
                {5, 6, 0}
        };

        double[][] matrixData2 = {
                {1, 2, 3},
                {0, 1, 4},
                {5, 6, 0}
        };

        // 求矩阵的逆
        double[][] result = matrixMultiply(matrixData1,matrixData2);
        printArray(result);
    }
    
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58

在这里插入图片描述

相关阅读:
第2篇机器学习基础 —（1）机器学习概念和方式
 系统架构常用的工具
 表面声波滤波器——SAW 基本介绍（1）
软件质量保护与测试（第2版）学习总结第十三章集成测试
 聊聊「低代码」的实践之路
 SpringBoot SpringBoot 运维实用篇 2 配置高级 2.1 临时属性
 jenkins+git持续集成配置
 前端三剑客 HTML、CSS、JavaScript 入门到上手
 IDL学习：语法基础-指针、链表
 基于PETALINUX的以太网调试
原文地址：https://blog.csdn.net/qq_44636569/article/details/133775937