【附代码】使用Shapely计算多边形外扩与收缩

作者：小猪快跑

基础数学&计算数学，从事优化领域5年+，主要研究方向：MIP求解器、整数规划、随机规划、智能优化算法

本文档介绍如何使用 Shapely Python 包 计算多边形外扩与收缩。

如有错误，欢迎指正。如有更好的算法，也欢迎交流！！！——@小猪快跑

相关文献

• The Shapely User Manual — Shapely 2.0.1 documentation

效果图

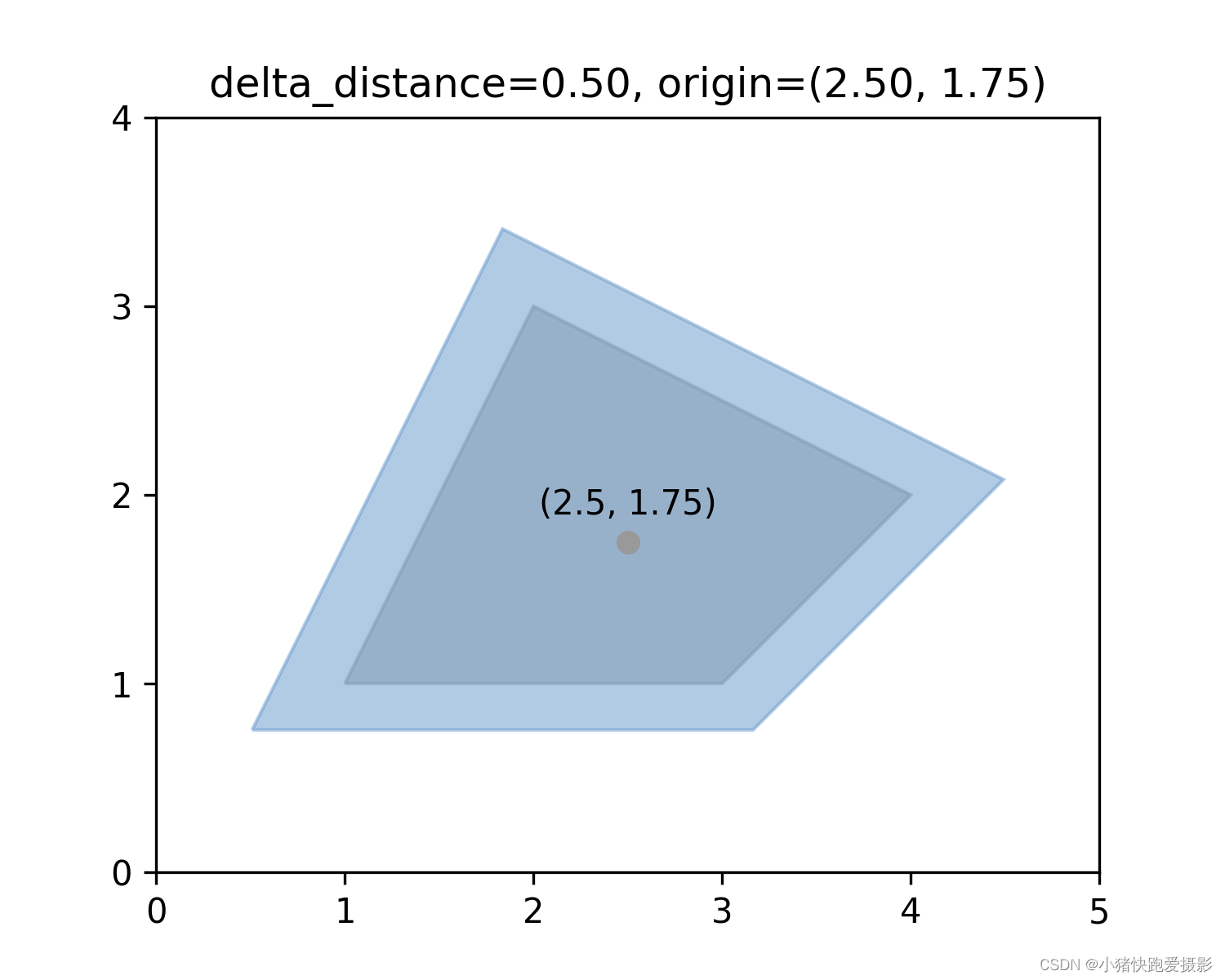
代码

# figures.py
from math import sqrt
from shapely import affinity

GM = (sqrt(5)-1.0)/2.0
W = 8.0
H = W*GM
SIZE = (W, H)

BLUE = '#6699cc'
GRAY = '#999999'
DARKGRAY = '#333333'
YELLOW = '#ffcc33'
GREEN = '#339933'
RED = '#ff3333'
BLACK = '#000000'


def add_origin(ax, geom, origin):
    x, y = xy = affinity.interpret_origin(geom, origin, 2)
    ax.plot(x, y, 'o', color=GRAY, zorder=1)
    ax.annotate(str(xy), xy=xy, ha='center',
                textcoords='offset points', xytext=(0, 8))


def set_limits(ax, x0, xN, y0, yN):
    ax.set_xlim(x0, xN)
    ax.set_xticks(range(x0, xN+1))
    ax.set_ylim(y0, yN)
    ax.set_yticks(range(y0, yN+1))
    ax.set_aspect("equal")
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

# main.py
import matplotlib.pyplot as plt
import numpy as np
from shapely.geometry import Point, LineString
from shapely import affinity, MultiPoint
from shapely.plotting import plot_polygon
from figures import BLUE, GRAY, set_limits, add_origin


def scale_line(point: Point, center_point: Point, delta_distance: float):
    distance = point.distance(center_point)
    distance_new = distance + delta_distance
    fact = distance_new / distance
    points = affinity.scale(LineString([(point.x, point.y), (center_point.x, center_point.y)]), xfact=fact, yfact=fact,
                            origin=(center_point.x, center_point.y)).coords[:]
    p0 = Point(points[0])
    p1 = Point(points[1])
    if p0.distance(center_point) > p1.distance(center_point):
        return p0
    return p1


if __name__ == '__main__':
    # 给定一些点先求凸包
    polygon = MultiPoint([(1, 1), (3, 1), (4, 2), (2, 3), (2, 2)]).convex_hull
    x, y = polygon.exterior.xy
    # 找到凸包的重心
    center_x = np.mean(x[1:])
    center_y = np.mean(y[1:])

    # 设置大致的外扩距离求出缩放系数fact（也可以直接设置比例fact）
    delta_distance = 0.5
    p0 = Point(x[0], y[0])
    p1 = Point(x[1], y[1])
    p0_new = scale_line(p0, Point(center_x, center_y), delta_distance)
    p1_new = scale_line(p1, Point(center_x, center_y), delta_distance)
    fact = p0_new.distance(p1_new) / p0.distance(p1)

    # 画图
    fig = plt.figure(1, figsize=(5, 4), dpi=300)
    ax = fig.add_subplot(111)
    plot_polygon(polygon, ax=ax, add_points=False, color=GRAY, alpha=0.5)
    polygon_new = affinity.scale(polygon, xfact=fact, yfact=fact, origin=(center_x, center_y))
    plot_polygon(polygon_new, ax=ax, add_points=False, color=BLUE, alpha=0.5)
    add_origin(ax, polygon, (center_x, center_y))
    ax.set_title(f"delta_distance={delta_distance:.2f}, origin=({center_x:.2f}, {center_y:.2f})")
    set_limits(ax, 0, 5, 0, 4)
    plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48