【数据结构】二叉树--顺序结构及实现 (堆)

目录

一 二叉树的顺序结构

二 堆的概念及结构

三 堆的实现

1 包含所有接口 (Heap.h)

2 初始化,销毁和交换（Heap.c)

3 向上调整（Heap.c)

4 插入（Heap.c)

​5 向下调整（Heap.c)

6 删除（Heap.c)

​7 打印（Heap.c)

8 返回堆顶（Heap.c)

9 判断是否为空（Heap.c)

10 测试（Test.c)

---

一 二叉树的顺序结构

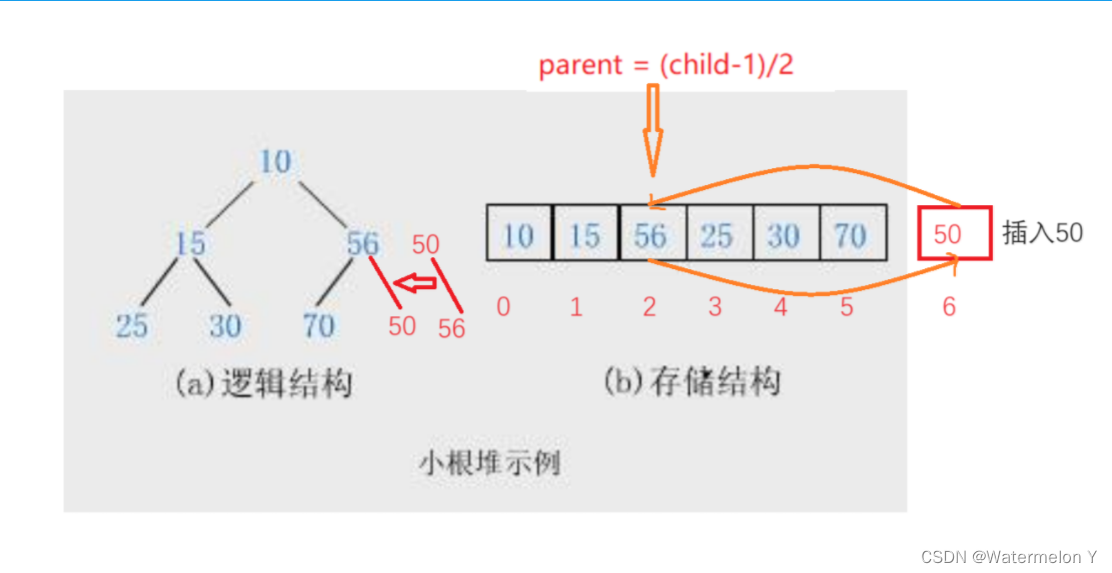
顺序结构存储就是使用数组来存储，一般使用数组只适合表示完全二叉树，因为不是完全二叉树会有空 间的浪费。而现实中使用中只有堆才会使用数组来存储，关于堆我们后面的章节会专门讲解。二叉树顺 序存储在物理上是一个数组，在逻辑上是一颗二叉树。

二 堆的概念及结构

如果有一个关键码的集合K = { ， ， ，…， }，把它的所有元素按完全二叉树的顺序存储方式存储 在一个一维数组中，并满足： <= 且 <= ( >= 且 >= ) i = 0，1， 2…，则称为小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。

堆的性质： 堆中某个节点的值总是不大于或不小于其父节点的值；

堆总是一棵完全二叉树。

三 堆的实现

1 包含所有接口 (Heap.h)

#pragma once
#include
#include
#include
#include
 
typedef int HPDataType;
typedef struct Heap
{
	HPDataType* a;
	int size;
	int capacity;
}HP;
 
//向上调整
void AdjustUp(HPDataType* a, int child);
 
//向下调整
void AdjustDown(HPDataType* a, int n, int parent);
 
//交换
void Swap(HPDataType* p1, HPDataType* p2);
//打印
void HeapPrint(HP* php);
//初始化
void HeapInit(HP* php);
//销毁
void HeapDestroy(HP* php);
//插入
void HeapPush(HP* php, HPDataType x);
//删除
void HeapPop(HP* php);
//返回堆顶
HPDataType HeapTop(HP* php);
//是否为空
bool HeapEmpty(HP* php);
 
 
 
 

2 初始化,销毁和交换（Heap.c)

#include"Heap.h"
 
void HeapInit(HP* php)
{
	assert(php);
	php->a = NULL;
	php->size = php->capacity = 0;
}
 
//销毁
void HeapDestroy(HP* php)
{
	assert(php);
	free(php->a);
	php->a = NULL;
	php->size = php->capacity = 0;
}
 
//交换
void Swap(HPDataType* p1, HPDataType* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}

 3 向上调整（Heap.c)

  时间复杂度 O(logN)

//向上调整
void AdjustUp(HPDataType* a, int child)
{
	int parent = (child - 1) / 2;
	while (child > 0)
	{
		if (a[child] < a[parent])//如果建大堆 就改成 a[child] > a[parent]
		{
			Swap(&a[child], &a[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

 4 插入（Heap.c)

//插入
void HeapPush(HP* php, HPDataType x)
{
	assert(php);
	if (php->size == php->capacity)
	{
		int newcapacity = (php->capacity == 0 ? 4 : php->capacity * 2);
		HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newcapacity);
		if (tmp == NULL)
		{
			perror("realloc fail");
			exit(-1);
		}
		php->a = tmp;
		php->capacity = newcapacity;
	}
 
	php->a[php->size] = x;
	php->size++;
	AdjustUp(php->a, php->size - 1);
}

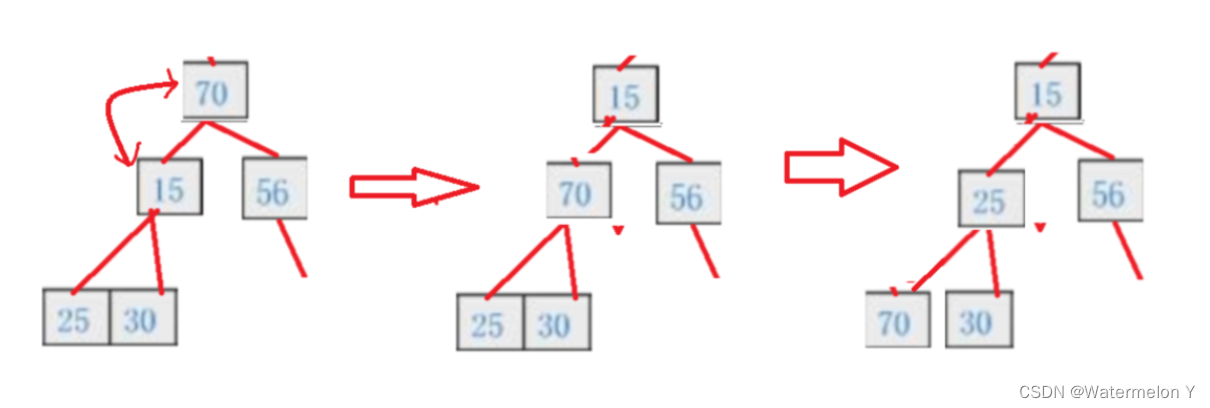
5 向下调整（Heap.c)

  时间复杂度 O(logN)

//向下调整
void AdjustDown(HPDataType* a, int n, int parent)
{
	int child = parent * 2 + 1;
	while (child < n)
	{
		//找小的那个孩子
		if (child+1 < n && a[child+1] < a[child])//child+1
		{
			child++;
		}
		if (a[child] < a[parent])//如果想大堆 改成>
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

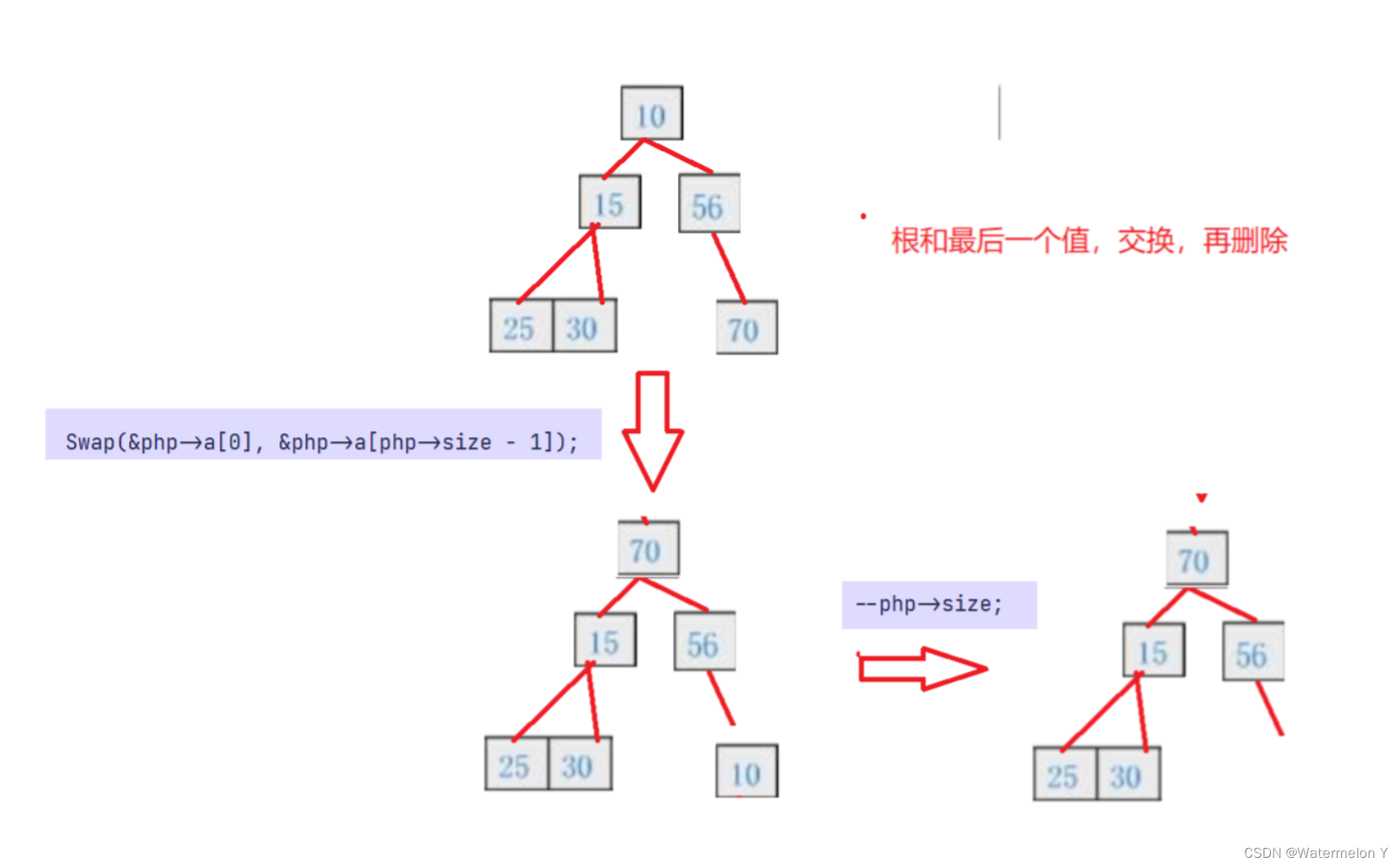
6 删除（Heap.c)

//删除
void HeapPop(HP* php)
{
	assert(php);
	assert(php->size > 0);
	Swap(&php->a[0], &php->a[php->size - 1]);
	php->size--;
 
	AdjustDown(php->a, php->size, 0);
}

7 打印（Heap.c)

//打印
void HeapPrint(HP* php)
{
	assert(php);
	for (size_t i = 0; i < php->size; i++)
	{
		printf("%d ", php->a[i]);
	}
	printf("\n");
}

8 返回堆顶（Heap.c)

//返回堆顶
HPDataType HeapTop(HP* php)
{
	assert(php);
	assert(php->size > 0);
	return php->a[0];
}

9 判断是否为空（Heap.c)

bool HeapEmpty(HP* php)
{
	assert(php);
	return php->size == 0;
}
 
//堆为空返回1 true
//堆不为空 返回0 false

10 测试（Test.c)

小堆情况（升序）

#include"Heap.h"
 
int main()
{
	int a[] = { 2,3,5,7,4,6,8,65,100,70,32,50,60 };
	HP hp;
	HeapInit(&hp);
	for (int i = 0; i < sizeof(a) / sizeof(int); i++)
	{
		HeapPush(&hp, a[i]);
	}
	HeapPrint(&hp);
 
	while (!HeapEmpty(&hp))
	{
		printf("%d ", HeapTop(&hp));
		HeapPop(&hp);
	}
 
	HeapDestroy(&hp);
 
	return 0;
}

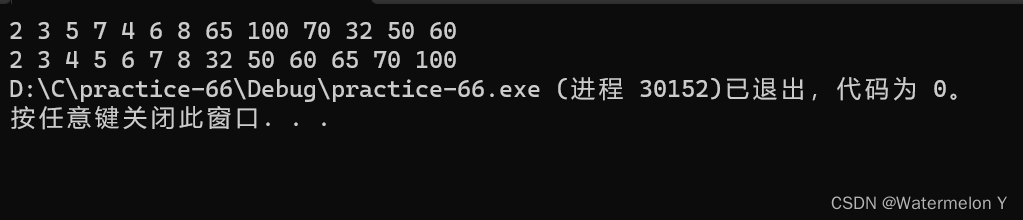
但是这种排序方式有明显的缺陷

1、先有一个堆的数据结构

2、空间复杂度复杂度的消耗

所以我们可以改进一下 用真正的堆排序 堆排序有很多细节 所以放在后面一节讲

本节很基础 与栈的实现有很多相似之处 大家也可以看我之前对栈的讲解 以此加深印象

继续加油!