C++算法之旅、09 力扣篇 | 常见面试笔试题（上）算法小白专用

刷题的目的是为了更好的理解数据结构与算法，更好的理解一些封装起来的库函数是怎么实现的，而不是简简单单的为了刷题而刷题。

时间、空间复杂度

事后统计法

提前写好算法代码和编好测试数据，在计算机上跑，通过最后得出的运行时间判断算法的效率

缺点

1. 太依赖计算机的软件和硬件等性能

   不同处理器、操作系统、编程语言、同环境下不同内存占用、CPU 使用率等会造成运行时间差异

2. 太依赖于测试数据集的规模

   输入 10 个数与 10w 个数差距很大

时间、空间复杂度

不依赖软硬件性能、测试数据集规模等外力影响就可以估算算法效率、判断算法优劣的度量指标

时间复杂度

时间复杂度是一个函数

大 O 表示法，表示的是算法有多快。 不代表算法真正运行时间，而是一种趋势。随着数据规模增大，算法代码运行时间变化的一种趋势

O(f(n)) ， f(n) 是算法代码执行的总步数，也叫操作数

只要找起“主导”作用的部分代码，这个主导就是最高的复杂度， 也就是执行次数最多的那部分 n 的量级

例如 : 数据集大小为 n，总步数为 (1+2n) 的算法的执行时间为 O(n)

时间复杂度	阶	f(n) 举例
常数复杂度	O(1)	1
对数复杂度	O(logn)	logn + 1
线性复杂度	O(n)	n + 1
线性对数复杂度	O(nlogn)	nlogn + 1
k 次复杂度	O(n ²)、O(n ³)、....	n ² + n +1
指数复杂度	O(2n)	2n + 1
阶乘复杂度	O(n!)	n! + 1

对数换底公式

对数时间复杂度可以忽略底数，直接用 O(logn) 来表示对数时间复杂度

logmN=logma∗logaN (a>0∧a≠1,m>0∧m≠1,N>0)log2n=log23∗log3nO(log2n)=O(log23∗log3n)=O(log3n)

最好、最坏、平均情况

除了数据集规模的影响，“数据集的具体情况”也会影响运行时间

• 最好情况就是在最理想的情况下，代码的时间复杂度
• 最坏情况就是在最差的情况下，代码的时间复杂度
• 平均情况，需要用概率来计算时间复杂度（加权平均值）

一般不用纠结各种情况，算时间复杂度算最坏情况即可

均摊时间复杂度

对一个数据结构进行一组连续操作中，大部分情况下时间复杂度都很低，只有个别情况下时间复杂度比较高，而且这些操作之间存在前后连贯的时序关系。

这时，我们可以将这一组操作放在一块儿分析，看是否能将较高时间复杂度那次操作的耗时，平摊到其他那些时间复杂度比较低的操作上。

而且，在能够应用均摊时间复杂度分析的场合，一般均摊时间复杂度就等于最好情况时间复杂度。

均摊时间复杂度就是一种特殊的平均时间复杂度。

空间复杂度

一种趋势，反映算法代码运行过程中临时变量占用的内存空间（不考虑代码区与输入数据）

O(f(n)) ， f(n) 是数据集规模 n 所占存储空间的函数

数组

线性数据结构。用连续一段内存空间，来存储相同数据类型数据的集合

• 优势：根据下标，随机存取元素
• 劣势：插入、删除操作，移动其他元素的过程很慢；数组越界
  • 最坏情况全部移动 O(n)

27 移除元素

27. 移除元素 - 力扣（LeetCode）

O(n2) 朴素

erase 方法复杂度 O(n)

class Solution {
   public:
    int removeElement(vector<int>& nums, int val) {
        int count = 0;
        for (auto i = nums.begin(); i < nums.end(); i++) {
            if (*i == val)
                nums.erase(i), i--;
            else
                count++;
        }
        return count;
    }
};

O(n) 双指针

快指针 fast 指向当前要和 val 对比的元素，慢指针 slow 指向将被赋值的位置

class Solution {
   public:
    int removeElement(vector<int>& nums, int val) {
        int slow, fast;
        slow = fast = 0;
        for (; fast < nums.size(); fast++) {
            if (nums[fast] != val) {
                nums[slow++] = nums[fast];
            }
        }
        return slow; 
    }
};

59 螺旋矩阵 II

59. 螺旋矩阵 II - 力扣（LeetCode）

O(n2) 状态移动

每个格子肯定都会走一遍，所以操作数 n2

class Solution {
   public:
    vector> generateMatrix(int n) {
        int state = 0;
        int dx[4] = {0, 1, 0, -1};
        int dy[4] = {1, 0, -1, 0};
        int count = 1, threshold = n * n;
        vector> v(n, vector(n));
        int x = 0, y = 0;
        while (count <= threshold) {
            v[x][y] = count++;
            int nx = x + dx[state], ny = y + dy[state];
            if (nx < 0 || nx >= n || ny < 0 || ny >= n || v[nx][ny] != 0) {
                state = (state + 1) % 4;
            }
            x += dx[state], y += dy[state];
        }
        return v;
    }
};

209 长度最小子数组

209. 长度最小的子数组 - 力扣（LeetCode）

O(n2) 滑动窗口

int const INF = 0x3f3f3f3f;

class Solution {
   public:
    int minSubArrayLen(int target, vector<int>& nums) {
        int ans = INF, a, b, sum = 0;
        a = b = 0;
        for (; b < nums.size(); b++) {
            sum += nums[b];
            while (a <= b && sum >= target) {
                ans = min(ans, b - a + 1);
                sum -= nums[a++];
            }
        }
        return ans == INF ? 0 : ans;
    }
};

977 有序数组的平方

977. 有序数组的平方 - 力扣（LeetCode）

O(n) 双指针

class Solution {
   public:
    vector<int> sortedSquares(vector<int>& nums) {
        vector<int> v(nums.size());
        int idx = nums.size() - 1;
        int left = 0, right = nums.size() - 1;
        while (left <= right) {
            v[idx--] = nums[left] * nums[left] > nums[right] * nums[right]
                           ? nums[left] * nums[left++]
                           : nums[right] * nums[right--];
        }
        return v;
    }
};

单链表

线性数据结构。用一组任意的存储单元存储线性表的数据元素，通过指针连接串联起来。

• 存储单元叫做 节点。含数据域和指针域

• 链表中的每个节点只包含一个指针域，这个链表就叫做单链表

• 第一个节点的存储位置叫做 头指针，最后一个节点的后继指针为空

  • 指向链表第一个结点的指针，如果有头结点就是指向头结点的指针
  • 头指针是链表必备元素，无论链表是否为空，头指针都不能为空

• 为了操作方便，在单链表的第一个节点前面加一个节点，称之为 虚拟头节点

  • 数据域没意义

• 插入、删除操作时间复杂度为 O(1)

• 应用场景

  • 多次插入删除操作
  • 不知道有多少个元素

双向链表

• 多了一个前驱指针 prev，指向前驱节点
• 在给定节点前插入删除，时间复杂度O(1)

实现方式

• 结构体法（速度慢）（LC 题解均用结构体）
• 数组模拟（速度快）

19 删除倒数第 N 节点

19. 删除链表的倒数第 N 个结点 - 力扣（LeetCode）

O(n) 双指针

形参头指针，为了方便操作，创建一个虚拟头节点 temp（哨兵节点）

b 先走，走了 n 格后，a 再走

class Solution {
   public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        int count = 0;
        ListNode *a, *b, *temp = new ListNode(0, head);
        a = temp;
        b = head;
        for (int i = 0; i < n; i++) b = b->next;
        while (b) {
            b = b->next;
            a = a->next;
        }
        a->next = a->next->next;
        ListNode* ans = temp->next;
        delete temp;
        return ans;
    }
};

24 两两交换

24. 两两交换链表中的节点 - 力扣（LeetCode）

O(n) 三指针

创建虚拟头结点、三个指针 a、b、c

class Solution {
   public:
    ListNode* swapPairs(ListNode* head) {
        ListNode* temp = new ListNode(0, head);
        ListNode *a = temp, *b = head, *c;
        while (b && b->next) {
            c = b->next;
            b->next = c->next;
            a->next = c;
            c->next = b;
            a = b;
            b = a->next;
        }

        ListNode* ans = temp->next;
        delete temp;
        return ans;
    }
};

25 K 个一组翻转

25. K 个一组翻转链表 - 力扣（LeetCode）

O(n) 翻转子链表

将每一段子链翻转并返回翻转后的头尾指针，并与主链相连

class Solution {
   public:
    pair Reverse(ListNode* head, ListNode* tail) {
        auto t = tail->next;
        auto a = head;
        while (t != tail) { //尾插法
            auto nex = a->next;
            a->next = t;
            t = a;
            a = nex;
        }
        return {tail, head};
    }

    ListNode* reverseKGroup(ListNode* head, int k) {
        auto hair = new ListNode(0, head);
        ListNode* pre = hair;
        while (head) {
            ListNode* tail = pre;
            for (int i = 0; i < k; i++) {
                tail = tail->next;
                if (!tail) {
                    return hair->next;
                }
            }
            ListNode* nex = tail->next;
            pair res = Reverse(head, tail);
            head = res.first;
            tail = res.second;
            pre->next = head;
            tail->next = nex;
            pre = tail;
            head = pre->next;
        }
        return hair->next;
    }
};

141 环形链表

141. 环形链表 - 力扣（LeetCode）

O(n) 快慢指针

有环情况下，当“快指针出现在慢指针后面”之后，每一次“快指针走两步、慢指针走一步”，相当于快指针和慢指针之间的相对距离减少 1 步

• 若是链表 无环，那么 fast 指针会先指向 Null
• 若是链表 有环，fast 和 slow 迟早会在环中相遇

class Solution {
   public:
    bool hasCycle(ListNode *head) {
        if (!head || !head->next) return false;
        ListNode *fast, *slow;
        fast = slow = head;
        while (fast && fast->next) {
            fast = fast->next->next;
            slow = slow->next;
            if (fast == slow) return true;
        }
        return false;
    }
};

142 环形链表 II

142. 环形链表 II - 力扣（LeetCode）

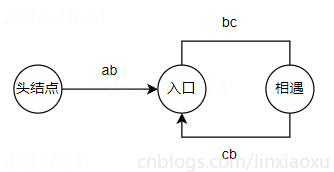
O(n) 数学思想

相遇时两指针走的距离。设 n 为 fast 指针走过的圈数

fast=ab+n(bc+cd)+bcslow=ab+bc∵fast=2∗slow∴ab+n(bc+cd)+bc=2ab+2bcn(bc+cd)=ab+bcab=(n−1)(bc+cd)+cd

同时从头节点和相遇节点出发的两个指针，每次走 1 步，最终会在入口处相遇

解题步骤

1. 快慢指针判断是否有环
2. 若有环，头节点、相遇节点同时出发两个指针，相遇的点即入口点

class Solution {
   public:
    ListNode *detectCycle(ListNode *head) {
        ListNode *fast, *slow;
        fast = slow = head;
        while (fast && fast->next) {
            fast = fast->next->next;
            slow = slow->next;
            if (fast == slow) {
                auto p1 = head;
                auto p2 = slow;
                while (p1 != p2) {
                    p1 = p1->next;
                    p2 = p2->next;
                }
                return p1;
            }
        }
        return nullptr;
    }
};

160 相交链表

160. 相交链表 - 力扣（LeetCode）

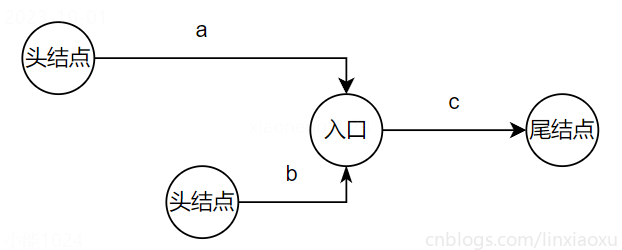
O(n+m) 数学思想

a+c+b=b+c+a

最坏情况下需要遍历两个链表，长度分别为 n、m，时间复杂度 O(n+m)

class Solution {
   public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        auto p1 = headA;
        auto p2 = headB;
        while (p1 && p2) {
            p1 = p1->next;
            p2 = p2->next;
        }
        if (!p1) p1 = headB;
        if (!p2) p2 = headA;
        while (p1 && p2) {
            p1 = p1->next;
            p2 = p2->next;
        }
        if (!p1) p1 = headB;
        if (!p2) p2 = headA;
        while (p1 && p2) {
            if (p1 == p2) return p1;
            p1 = p1->next;
            p2 = p2->next;
        }
        return nullptr;
    }
};

206 翻转链表

https://leetcode.cn/problems/reverse-linked-list/

O(n) 头插法

虚拟头结点，在其后头插法

class Solution {
   public:
    ListNode* reverseList(ListNode* head) {
        auto hair = new ListNode(0);
        auto p1 = head;
        while (p1) {
            auto nex = p1->next;
            p1->next = hair->next;
            hair->next = p1;
            p1 = nex;
        }
        return hair->next;
    }
};

707 设计链表

707. 设计链表 - 力扣（LeetCode）

考查代码功底

虚拟头结点 hair 方便操作单链表

struct LS {
    LS *next;
    int val;
    LS(int val) : val(val), next(nullptr) {}
    LS(int val, LS *next) : val(val), next(next) {}
};

class MyLinkedList {
   public:
    LS *hair;

    MyLinkedList() { hair = new LS(0); }

    int get(int index) {
        if (!hair->next) return -1;
        auto p1 = hair;
        for (int i = 0; i <= index; i++) {
            p1 = p1->next;
            if (!p1) return -1;
        }
        return p1->val;
    }

    void addAtHead(int val) {
        LS *p = new LS(val, hair->next);
        hair->next = p;
    }

    void addAtTail(int val) {
        auto p1 = hair;
        while (p1->next) {
            p1 = p1->next;
        }
        LS *p = new LS(val, nullptr);
        p1->next = p;
    }

    void addAtIndex(int index, int val) {
        auto p1 = hair;
        for (int i = 0; i < index; i++) {
            p1 = p1->next;
            if (!p1) return;
        }
        LS *p = new LS(val, p1->next);
        p1->next = p;
    }

    void deleteAtIndex(int index) {
        auto p1 = hair;
        for (int i = 0; i < index; i++) {
            p1 = p1->next;
            if (!p1) return;
        }
        if (p1->next) {
            LS *temp = p1->next;
            p1->next = temp->next;
            delete temp;
        }
    }
};

栈

线性数据结构。仅在表尾（栈顶）进行插入删除操作的线性表。后进先出 LIFO（Last In First Out）

• 顺序存储的栈叫顺序栈。使用数组实现（-1 下标表示空栈）
  • 元素个数是固定值，存在栈满情况
• 链式存储的栈叫链栈。使用单链表实现
  • 不存在栈满情况

20 有效括号

20. 有效的括号 - 力扣（LeetCode）

O(n) 栈 朴素

int const N = 1e4 + 10;

class Solution {
   public:
    char stack[N];
    int top = -1;
    bool isValid(string s) {
        top = -1;
        for (int i = 0; i < s.size(); i++) {
            if (s[i] == ']') {
                if (top == -1) return false;
                if (stack[top] != '[')
                    return false;
                else
                    top--;
            } else if (s[i] == '}') {
                if (top == -1) return false;
                if (stack[top] != '{')
                    return false;
                else
                    top--;
            } else if (s[i] == ')') {
                if (top == -1) return false;
                if (stack[top] != '(')
                    return false;
                else
                    top--;
            } else {
                stack[++top] = s[i];
            }
        }
        return top == -1;
    }
};

O(n) 栈 STL

class Solution {
   public:
    bool isValid(string s) {
        int n = s.size();
        if (n % 2 == 1) {
            return false;
        }

        unordered_map<char, char> pairs = {{')', '('}, {']', '['}, {'}', '{'}};
        stack<char> stk;
        for (char ch : s) {
            if (pairs.count(ch)) {
                if (stk.empty() || stk.top() != pairs[ch]) {
                    return false;
                }
                stk.pop();
            } else {
                stk.push(ch);
            }
        }
        return stk.empty();
    }
};

150 逆波兰表达式

150. 逆波兰表达式求值 - 力扣（LeetCode）

O(n) 栈 STL

用栈存储数，遇到操作符就拿出两个数计算

class Solution {
   public:
    int evalRPN(vector& tokens) {
        stack<int> s;
        for (auto& c : tokens) {
            if (isdigit(c[0]) || c.length() > 1) {  // 考虑 -11 这种情况
                s.push(atoi(c.c_str()));
            } else {
                int b = s.top();
                s.pop();
                int a = s.top();
                s.pop();
                if (c == "-") {
                    s.push(a - b);
                } else if (c == "+") {
                    s.push(a + b);
                } else if (c == "*") {
                    s.push(a * b);
                } else if (c == "/") {
                    s.push(a / b);
                }
            }
        }
        return s.top();
    }
};

232 用栈实现队列

232. 用栈实现队列 - 力扣（LeetCode）

O(1) 两栈 STL

两个栈，一个负责输入，一个负责输出。pop、peek 操作均摊时间复杂度 O(1)

• 每个元素最多入栈、出栈各两次

class MyQueue {
   public:
    stack<int> s1, s2;

    MyQueue() {}

    void push(int x) { s1.push(x); }

    int pop() {
        if (s2.empty())
            while (!s1.empty()) {
                s2.push(s1.top());
                s1.pop();
            }
        int temp = s2.top();
        s2.pop();
        return temp;
    }

    int peek() {
        if (s2.empty())
            while (!s1.empty()) {
                s2.push(s1.top());
                s1.pop();
            }
        int temp = s2.top();
        return temp;
    }

    bool empty() { return s1.empty() && s2.empty(); }
};

1047 删除字符串中的所有相邻重复项

O(n) 栈 字符串

栈 20 有效括号 衍生题

string 类型也是有栈的特性的！

class Solution {
   public:
    string removeDuplicates(string s) {
        string ans;
        for (auto c : s) {
            if (!ans.empty() && ans.back() == c)
                ans.pop_back();
            else
                ans.push_back(c);
        }
        return ans;
    }
};

队列

线性数据结构。仅在队头插入，队尾删除的线性表。先进先出 FIFO（First In First Out）

• 顺序存储
  • 初始化 hh = 0，tt = 0 （指向下一个要填充的位置）
  • 循环队列：判断队列满的条件 (tail + 1) % n = head
    • 两种情况：正常占用完 或 发生循环
• 链式存储
  • 当 head 与 tail 指向同一节点，为空队列

225 用队列实现栈

225. 用队列实现栈 - 力扣（LeetCode）

O(n) 两队列 STL

一个主队列和一个辅助队列，每次入栈操作时，将新元素添加到辅助队列，再依次将主队列的元素出队列，依次加入辅助队列，最后将主队列与辅助队列互换。

入栈操作 O(n)，其余操作都是 O(1)

class MyStack {
   public:
    queue<int> q1, q2;
    MyStack() {}

    void push(int x) {
        q2.push(x);
        while (!q1.empty()) {
            q2.push(q1.front());
            q1.pop();
        }
        swap(q1, q2);
    }

    int pop() {
        int temp = q1.front();
        q1.pop();
        return temp;
    }

    int top() { return q1.front(); }

    bool empty() { return q1.empty(); }
};

O(n) 单队列 STL

一个主队列，插入操作时，先插入，然后弹出前 n 个元素并重新放入当前队列

入栈操作 O(n)，其余操作都是 O(1)

#include 

using namespace std;

class MyStack {
   public:
    queue<int> q1;
    MyStack() {}

    void push(int x) {
        int n = q1.size();
        q1.push(x);
        for (int i = 0; i < n; i++) {
            q1.push(q1.front());
            q1.pop();
        }
    }

    int pop() {
        int temp = q1.front();
        q1.pop();
        return temp;
    }

    int top() { return q1.front(); }

    bool empty() { return q1.empty(); }
};

239 滑动窗口最大值

239. 滑动窗口最大值 - 力扣（LeetCode）

O(n) 单调队列 STL

维护一个单调递减的双端队列，队列存的是下标

// class Solution {
//    public:
//     vector maxSlidingWindow(vector& nums, int k) {
//         deque q;
//         vector ans;
//         for (int i = 0; i < k; i++) {
//             while (!q.empty() && nums[i] >= nums[q.back()]) q.pop_back();
//             q.push_back(i);
//         }
//         ans.push_back(nums[q.front()]);
//         for (int i = k; i < nums.size(); i++) {
//             if (q.front() <= i - k) q.pop_front();
//             while (!q.empty() && nums[i] >= nums[q.back()]) q.pop_back();
//             q.push_back(i);
//             ans.push_back(nums[q.front()]);
//         }
//         return ans;
//     }
// };

class Solution {
   public:
    vector maxSlidingWindow(vector& nums, int k) {
        deque q;
        vector ans;
        q.push_back(0);  // 解决下面的问题
        for (int i = 0; i < nums.size(); i++) {
            if (i - q.front() + 1 > k) q.pop_front();
            // 第一次循环，队列为空的时候，左值为false，必定会算右值，发生异常
            while (!q.empty() && nums[q.back()] <= nums[i]) q.pop_back();
            q.push_back(i);
            if (i >= k - 1) ans.push_back(nums[q.front()]);
        }
        return ans;
    }
};

字符串

字符串是由零个或多个字符组成的有限序列

• 序列：相邻字符有前驱与后继
• 空串：0 个字符组成的字符串，“”
• 空格串：只含 0 个或多个空格的字符串
• 子串：字符串中任意个数连续字符组成的子序列
• 主串：包含子串的字符串
• 在 C/C++ 中，用 ’\0‘ 表示字符串结束标记

存储方式

• 定长顺序存储：存储空间确定，长度不变，超过则截断
• 堆区存储（动态数组）
• 链式存储：每个节点存储一个或多个字符

JZ05 替换空格

剑指 05 替换空格

class Solution {
   public:
    string replaceSpace(string s) {
        for (int i = 0; i < s.size(); i++) {
            if (s[i] == ' ') {
                s[i] = '%';
                s.insert(i + 1, "20");
            }
        }
        return s;
    }
};

JZ58 左旋转字符串

剑指 58 左旋转字符串

class Solution {
   public:
    string LeftRotateString(string str, int n) {
        if (n <= 0 || str.size() <= 1) return str;
        n = n % str.size();
        //return str.substr(n) + str.substr(0, n);
        reverse(str.begin(), str.end());
        reverse(str.begin(), str.begin() + str.size() - n);
        reverse(str.begin() + str.size() - n, str.end());
        return str;
    }
};

151 反转字符串中的单词

151. 反转字符串中的单词 - 力扣（LeetCode）

从后往前、双指针

class Solution {
   public:
    string reverseWords(string s) {
        s = ' ' + s;
        int n = s.size();
        string ans;
        for (int left = n - 1, right = n; left >= 0; left--) {
            if (s[left] == ' ') {
                if (left + 1 < right) {
                    ans += s.substr(left + 1, right - left - 1);
                    ans += ' ';
                }
                right = left;
            }
        }
        return ans.substr(0, ans.size() - 1);
    }
};

分解问题、双指针

1. 先去除空格
2. 整体反转
3. 每个单词反转

class Solution {
   public:
    string reverseWords(string s) {
        int k;
        // 删开头
        for (k = 0; k < s.size(); ++k)
            if (s[k] != ' ') break;
        s.erase(s.begin(), s.begin() + k);

        // 删末尾
        for (k = s.size() - 1; k >= 0; --k)
            if (s[k] != ' ') break;
        s.erase(s.begin() + k + 1, s.end());

        // 删中间
        int i = 0, j = 0;
        while (j < s.size()) {
            // abc   abc
            if (s[j] == ' ' && s[j - 1] == ' ')
                j++;
            else {
                s[i] = s[j];
                i++;
                j++;
            }
        }
        s.resize(i);

        // 反转字符串
        reverse(s.begin(), s.end());

        // 反转单词
        int tag = 0;
        for (i = 0; i < s.size(); ++i) {
            if (s[i] == ' ') {
                reverse(s.begin() + tag, s.begin() + i);
                tag = i + 1;
            }
        }
        reverse(s.begin() + tag, s.begin() + i);
        return s;
    }
};

344 反转字符串

344. 反转字符串 - 力扣（LeetCode）

O(n) 双指针

class Solution {
   public:
    void reverseString(vector<char>& s) {
        int left, right;
        left = 0;
        right = s.size() - 1;
        while (left < right) {
            swap(s[left++], s[right--]);
        }
    }
};

541 反转字符串 II

541. 反转字符串 II - 力扣（LeetCode）

O(n) 双指针

class Solution {
   public:
    void reverse(string &s, int left, int right) {
        while (left < right) {
            swap(s[left++], s[right--]);
        }
    }

    string reverseStr(string s, int k) {
        int i = 2 * k;
        for (; i <= s.size(); i += 2 * k) {
            reverse(s, i - 2 * k, i - k - 1);
        }
        i -= 2 * k;
        if (s.size() - i <= k)
            reverse(s, i, s.size() - 1);
        else if (s.size() - i > k)
            reverse(s, i, i + k - 1);
        return s;
    }
};

哈希表

散列表，Hash Table。不用一些无用的比较，直接通过关键字 key 就能找到它的存储位置。 主要是面向查找的存储结构，简化比较的过程，提高了效率

存储位置 = f(关键字)。f 为哈希函数，每个 key 被对应到 0 ~ N-1 的范围内，并且放在合适的位置

处理哈希冲突常用方法

• 开放寻址法：发生冲突，就选择另外一个可用位置
  • 线性探测法
    • f(key) = (f(key) + di) % m (di = 1, 2, 3, ... , m-1)
    • 低插入和查找效率
  • 二次探测法
    • f(key) = (f(key) + di) % m (di = 1 ², -1 ², 2 ², -2 ², ..., q ², -q ², q ≤ m/2)
    • 对线性探测法的改进
• 再哈希函数法
  • 使用一组哈希函数（明显增加计算时间）
• 拉链法
  • 邻接表法
  • 插入 O(1) 查找 O(k)

1 两数之和

1. 两数之和 - 力扣（LeetCode）

O(n) 哈希表 STL

空间换时间。键存数，值存下标。遍历一遍 nums 找数组中是否存在 target - x

class Solution {
   public:
    vector<int> twoSum(vector<int>& nums, int target) {
        unordered_map<int, int> hash;
        for (int i = 0; i < nums.size(); i++) {
            int b = target - nums[i];
            if (hash.count(b)) {
                return {hash[b], i};  // 题目给的数据一定会返回
            } else {
                hash[nums[i]] = i;
            }
        }
        return {};  // 防报错
    }
};

15 三数之和

15. 三数之和 - 力扣（LeetCode）

O(n2) 双指针

1. 先排序，避免重复运算
2. 列举每一项，每一项后段通过双指针查找每一次可能的结果
3. 去重

class Solution {
   public:
    vectorint>> threeSum(vector<int>& nums) {
        sort(nums.begin(), nums.end());
        vectorint>> ans;
        for (int i = 0; i < nums.size(); i++) {
            if (i > 0 && nums[i] == nums[i - 1]) continue;
            if (nums[i] > 0) break;
            int left = i + 1, right = nums.size() - 1;
            while (left < right) {
                int sum = nums[i] + nums[left] + nums[right];
                if (sum < 0)
                    left++;
                else if (sum > 0)
                    right--;
                else {
                    ans.push_back({nums[i], nums[left], nums[right]});
                    left++, right--;
                }
            }
        }
        sort(ans.begin(), ans.end());
        ans.erase(unique(ans.begin(), ans.end()), ans.end());
        return ans;
    }
};

O(n2) 哈希表 超时

列举每一项 a1，并列举a1之后的每一项 bi当前 b1不存在于哈希表⇒存储−a1−b1当列举到新 b2 时，若存在于哈希表，存在三元组 {a1,−a1−b2,b2} 满足三数之和为 0−a1−b2=b1

class Solution {
   public:
    vectorint>> threeSum(vector<int>& nums) {
        sort(nums.begin(), nums.end());
        vectorint>> ans;
        unordered_map<int, int> hash;
        for (int i = 0; i < nums.size(); i++) {
            if (i > 0 && nums[i] == nums[i - 1]) continue;
            hash.clear();
            for (int j = i + 1; j < nums.size(); j++) {
                if (hash.count(nums[j])) {
                    ans.push_back({nums[i], -nums[i] - nums[j], nums[j]});
                } else
                    hash[-nums[i] - nums[j]] = 1;
            }
        }
        sort(ans.begin(), ans.end());
        ans.erase(unique(ans.begin(), ans.end()), ans.end());
        return ans;
    }
};

202 快乐数

202. 快乐数 - 力扣（LeetCode）

O(logn) 哈希表 STL

将正整数替换为它每个位置上的数字的平方和 的过程中，判断新出现的正整数是否曾经出现过

时间复杂度

• 求每个位置上数字的平方和为 O(logn)
• 判断元素是否在集合中 O(1)

class Solution {
   public:
    int sum(int n) {
        int sum = 0;
        while (n) {
            int i = n % 10;
            sum += i * i;
            n /= 10;
        }
        return sum;
    }

    bool isHappy(int n) {
        unordered_set<int> hash;
        hash.insert(n);
        while (n != 1) {
            n = sum(n);
            if (hash.count(n))
                return false;
            else
                hash.insert(n);
        }
        return true;
    }
};

242 有效的字母异位词

242. 有效的字母异位词 - 力扣（LeetCode）

O(n+m) 哈希表 STL

1. 遍历两个字符串的所有字符，统计进哈希表中，一个加，一个减
2. 遍历完后，哈希表有字符个数不为 0 说明不是有效的字母异位词

class Solution {
   public:
    bool isAnagram(string s, string t) {
        unordered_map<char, int> hash;
        for (int i = 0; i < s.size(); i++) hash[s[i]]++;
        for (int i = 0; i < t.size(); i++) hash[t[i]]--;
        for (auto k : hash) {
            if (k.second != 0) return false;
        }
        return true;
    }
};

349 两个数组的交集

349. 两个数组的交集 - 力扣（LeetCode）

O(n+m) 哈希表 STL

解决重复元素：直接数组去重 或 添加进 res 后在哈希表上删除该元素

class Solution {
   public:
    vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
        // sort(nums1.begin(), nums1.end());
        // nums1.erase(unique(nums1.begin(), nums1.end()), nums1.end());
        // sort(nums2.begin(), nums2.end());
        // nums2.erase(unique(nums2.begin(), nums2.end()), nums2.end());
        unordered_set<int> hash;
        for (int i = 0; i < nums1.size(); i++) hash.insert(nums1[i]);
        vector<int> ans;
        for (int i = 0; i < nums2.size(); i++)
            if (hash.count(nums2[i]))
                ans.push_back(nums2[i]), hash.erase(nums2[i]);
        return ans;
    }
};

383 赎金信

383. 赎金信 - 力扣（LeetCode）

O(n+m) 哈希表 数组

242 有效的字母异位词 衍生题

class Solution {
   public:
    int hash[30];
    bool canConstruct(string ransomNote, string magazine) {
        memset(hash, 0, sizeof hash);
        for (int i = 0; i < magazine.size(); i++) hash[magazine[i] - 'a']++;
        for (int i = 0; i < ransomNote.size(); i++) {
            if (!hash[ransomNote[i] - 'a']) return false;
            hash[ransomNote[i] - 'a']--;
        }
        return true;
    }
};

454 四数相加Ⅱ

454. 四数相加 II - 力扣（LeetCode）

O(n2) 哈希表 STL

统计次数。没要求找出不重复的四元组，不需要考虑去重，列举每一种情况即可

1. 分组 nums1 和 nums2 一组，nums3 和 nums4 一组
2. 遍历第一组，哈希表键存和，值存次数
3. 遍历第二组，哈希表找 -nums3 [i]-nums4 [j] 的元素

class Solution {
   public:
    int fourSumCount(vector<int>& nums1, vector<int>& nums2, vector<int>& nums3,
                     vector<int>& nums4) {
        unordered_map<int, int> hash;
        int ans = 0;
        for (int a : nums1)
            for (int b : nums2) hash[a + b]++;
        for (int a : nums3)
            for (int b : nums4)
                if (hash[-a - b]) ans += hash[-a - b];
        return ans;
    }
};

575 分糖果

575. 分糖果 - 力扣（LeetCode）

O(n) 哈希表 STL

class Solution {
   public:
    int distributeCandies(vector<int>& candyType) {
        int count = 0;
        unordered_set<int> hash;
        for (auto c : candyType) {
            if (!hash.count(c)) count++, hash.insert(c);
        }
        int n = candyType.size() / 2;
        if (count >= n)
            return n;
        else
            return count;
    }
};

// 简洁写法
class Solution {
   public:
    int distributeCandies(vector<int>& candyType) {
        return min(
            unordered_set<int>(candyType.begin(), candyType.end()).size(),
            candyType.size() / 2);
    }
};

递归

找出重复的子问题（递推公式） + 终止条件

• 有时候需要两个或者多个终止条件
• 栈溢出：设置递归调用深度，超过深度就退出
• 重复计算：保存已经求解过的值， 判重 + 记录结果 （记忆化搜索）

迭代

迭代法就是不断地将旧的变量值，递推计算新的变量值

• 栈（前中后序遍历）
• 队列（层序遍历）

分治

• 划分（Divide）：将原问题划分为规模较小的子问题，子问题相互独立，与原问题形式相同

• 求解（Conquer）：递归的求解划分之后的子问题

• 合并（Combine）：非必须。有些问题涉及合并子问题的解，将子问题的解合并成原问题的解。有的问题则不需要，只是求出子问题的解即可

二叉树

非线性结构典型代表

• 树（连通、无回路、无向图）
  • 兄弟节点：一个节点的所有子节点之间互相称为 兄弟节点
  • 根节点：没有父节点的节点
  • 叶节点：没有子节点的节点
  • 内部节点：除根节点与叶节点以外的节点
  • 祖宗节点：从根节点到该节点 之前 经过的 所有节点
  • 子孙节点：从某节点 直至 叶子节点的 所有节点
  • 子树：以某个节点为根节点的树称为该节点的子树
    • 各个子树一定不互相交
  • 层次：根开始第一层，子节点第二层，依次往下类推
  • 深度：跟层次类似，从上往下看。最大深度为最大层数
  • 高度：与深度相反，从下往上看
• 种类
  • 二叉树：每个节点最多只有两个叉的树叫二叉树
  • 满二叉树：除了叶子节点以外的所有节点都有两个叉
    • 深度为 k , 总节点数 2k−1
    • 同深度二叉树中，满二叉树节点个数最多
  • 完全二叉树：除了最底层，其余每一层节点都是满的
    • 最底层节点集中在该层最左边位置
    • 最后一层最少有 1 个叶子节点，最多 2k−1 个节点
  • 二叉搜索树（排序树、查找树）
    • 若左子树不空，那左子树所有节点的值均 < 根节点的值。
    • 若右子树不空，那右子树所有节点的值均 > 根节点的值。
    • 左右子树也均为二叉搜索树
• 存储方式
  • 顺序存储：数组
  • 链式存储：一个数据域+两个指针
• 遍历方式
  • 前序遍历：根左右
  • 中序遍历：左根右
  • 后序遍历：左右根
  • 层次遍历

144 前序遍历

144. 二叉树的前序遍历 - 力扣（LeetCode）

O(n) 递归

class Solution {
   public:
    void preOrder(TreeNode* root, vector<int>& ans) {
        if (!root) return;
        ans.push_back(root->val);
        preOrder(root->left, ans);
        preOrder(root->right, ans);
    }

    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> ans;
        preOrder(root, ans);
        return ans;
    }
};

O(n) 迭代

前序遍历中访问节点的顺序和处理节点的顺序是一致的

• 初始化维护一个栈，将根节点入栈

• 当栈不为空时

• • 弹出栈顶元素 node，将节点值加入结果数组中
  • 若 node 的右子树不为空，右子树入栈
  • 若 node 的左子树不为空，左子树入栈

class Solution {
   public:
    vector<int> preorderTraversal(TreeNode* root) {
        if (!root) return {};
        vector<int> ans;
        stack stk;
        stk.push(root);
        while (!stk.empty()) {
            auto t = stk.top();
            stk.pop();
            ans.push_back(t->val);
            if (t->right) stk.push(t->right);
            if (t->left) stk.push(t->left);
        }
        return ans;
    }
};

94 中序遍历

94. 二叉树的中序遍历 - 力扣（LeetCode）

O(n) 递归

class Solution {
   public:
    void inOrder(TreeNode* root, vector<int>& ans) {
        if (!root) return;
        inOrder(root->left, ans);
        ans.push_back(root->val);
        inOrder(root->right, ans);
    }

    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> ans;
        inOrder(root, ans);
        return ans;
    }
};

O(n) 迭代 ⭐

中序遍历中访问节点的顺序和处理节点的顺序不一致。处理节点是在遍历完左子树之后

从根节点开始，一层层的遍历，找到左子树最左的那个节点，从它开始处理节点

• 初始化一个空栈。

• 当【根节点不为空】或者【栈不为空】时，从根节点开始

• • 若当前节点有左子树，一直遍历左子树，每次将当前节点压入栈中
  • 若当前节点无左子树，从栈中弹出该节点，尝试访问该节点的右子树

class Solution {
   public:
    vector<int> inorderTraversal(TreeNode* root) {
        if (!root) return {};
        vector<int> ans;
        stack stk;
        while (root || !stk.empty()) {
            if (root) {
                stk.push(root);
                root = root->left;
            } else {
                root = stk.top();
                stk.pop();
                ans.push_back(root->val);
                root = root->right;
            }
        }
        return ans;
    }
};

145 后序遍历

145. 二叉树的后序遍历 - 力扣（LeetCode）

O(n) 递归

class Solution {
   public:
    void postOrder(TreeNode* root, vector<int>& ans) {
        if (!root) return;
        postOrder(root->left, ans);
        postOrder(root->right, ans);
        ans.push_back(root->val);
    }

    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> ans;
        postOrder(root, ans);
        return ans;
    }
};

O(n) 迭代 ⭐

• 初始化一个空栈

• 当【根节点不为空】或者【栈不为空】时，从根节点开始

• • 每次将当前节点压入栈中，如果当前节点有左子树，就往左子树跑，没有左子树就往右子树跑
  • 若当前节点无左子树也无右子树，从栈中弹出该节点，如果当前节点是上一个节点（即弹出该节点后的栈顶元素）的左节点，尝试访问上个节点的右子树，如果不是，那当前栈的栈顶元素继续弹出

class Solution {
   public:
    vector postorderTraversal(TreeNode* root) {
        if (!root) return {};
        stack stk;
        vector ans;
        while (root || !stk.empty()) {
            while (root) {
                stk.push(root);
                if (root->left)
                    root = root->left;
                else
                    root = root->right;
            }
            auto t = stk.top();
            stk.pop();
            ans.push_back(t->val);
            if (!stk.empty() && t == stk.top()->left) {
                root = stk.top()->right;
            }
        }
        return ans;
    }
};

102 层序遍历

102. 二叉树的层序遍历 - 力扣（LeetCode）

O(n) 迭代 队列

队列保存每一层的所有节点，将该层节点全部出队，把出队节点各自子节点入队列

class Solution {
   public:
    vectorint>> levelOrder(TreeNode* root) {
        if (!root) return {};
        queue q;
        q.push(root);
        vectorint>> ans;
        while (!q.empty()) {
            int n = q.size();
            vector<int> line;
            for (int i = 0; i < n; i++) {
                auto t = q.front();
                q.pop();
                if (t->left) q.push(t->left);
                if (t->right) q.push(t->right);
                line.push_back(t->val);
            }
            ans.push_back(line);
        }
        return ans;
    }
};

100 相同的树

100. 相同的树 - 力扣（LeetCode）

O(min(n,m)) 递归

p 子树 n 个节点，q 子树 m 个节点

终止条件

• 节点为空
  • 左右节点都为空，此时相当于只有个头节点，是相同的
  • 左节点为空，右节点不为空，显然不相同
  • 左节点不为空，右节点为空，显然不相同
• 节点不为空
  • 两节点值不同，不相同

递推公式

• p 树的左子树和 q 树的左子树，p 树的右子树和 q 树的右子树是否相等

class Solution {
   public:
    bool isSameTree(TreeNode* p, TreeNode* q) {
        // 终止条件
        if (!p && !q)
            return true;
        else if (!p && q)
            return false;
        else if (p && !q)
            return false;
        else if (p->val != q->val)
            return false;
        // 递推公式
        bool b1 = isSameTree(p->left, q->left);
        bool b2 = isSameTree(p->right, q->right);
        return b1 && b2;
    }
};

O(n) 迭代 层序

每次取相邻的两个 p、q 做比较。并依次将 p 的左节点和 q 的左节点入队列，p 的右节点和 q 的右节点入队列

class Solution {
   public:
    bool isSameTree(TreeNode* p, TreeNode* q) {
        queue que;
        que.push(p);
        que.push(q);
        while (!que.empty()) {
            int n = que.size();
            auto t1 = que.front();
            que.pop();
            auto t2 = que.front();
            que.pop();
            if (!t1 && !t2)
                continue;  // 不能返回，当前层还没有遍历完
            else if (!t1 && t2)
                return false;
            else if (t1 && !t2)
                return false;
            else if (t1->val != t2->val)
                return false;
            que.push(t1->left);
            que.push(t2->left);
            que.push(t1->right);
            que.push(t2->right);
        }
        return true;
    }
};

101 对称二叉树

101. 对称二叉树 - 力扣（LeetCode）

O(n) 递归

class Solution {
   public:
    bool compareTree(TreeNode* left, TreeNode* right) {
        if (!left && !right)
            return true;
        else if (!left && right)
            return false;
        else if (left && !right)
            return false;
        else if (left->val != right->val)
            return false;
        bool l = compareTree(left->left, right->right);
        bool r = compareTree(left->right, right->left);
        return l && r;
    }

    bool isSymmetric(TreeNode* root) {
        if (!root) return true;

        return compareTree(root->left, root->right);
    }
};

O(n) 迭代 层序

class Solution {
   public:
    bool compareTree(TreeNode* left, TreeNode* right) {
        queue q;
        q.push(left);
        q.push(right);
        while (!q.empty()) {
            int n = q.size();
            auto t1 = q.front();
            q.pop();
            auto t2 = q.front();
            q.pop();
            if (!t1 && t2)
                return false;
            else if (t1 && !t2)
                return false;
            else if (!t1 && !t2)
                continue;
            else if (t1->val != t2->val)
                return false;
            q.push(t1->left);
            q.push(t2->right);
            q.push(t1->right);
            q.push(t2->left);
        }
        return true;
    }

    bool isSymmetric(TreeNode* root) {
        if (!root) return true;
        return compareTree(root->left, root->right);
    }
};

104 二叉树的最大深度

104. 二叉树的最大深度 - 力扣（LeetCode）

O(n) 递归

自底向上，后序遍历

class Solution {
   public:
    int maxDepth(TreeNode* root) {
        if (!root) return 0;
        int left = maxDepth(root->left);
        int right = maxDepth(root->right);
        return max(left, right) + 1;
    }
};

O(n) 迭代 层序

队列实现层序遍历

class Solution {
   public:
    int maxDepth(TreeNode* root) {
        if (!root) return 0;
        int depth = 0;
        queue q;
        q.push(root);
        while (!q.empty()) {
            int n = q.size();
            for (int i = 0; i < n; i++) {
                auto t = q.front();
                q.pop();
                if (t->left) q.push(t->left);
                if (t->right) q.push(t->right);
            }
            depth++;
        }
        return depth;
    }
};

111 二叉树最小深度 ⭐

111. 二叉树的最小深度 - 力扣（LeetCode）

O(n) 递归

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。假设二叉树只有左子树有叶子节点，而右子树是空的，没有叶子节点，也就不存在从根节点到右子树的最小深度。如果采用 104 题写法，会把当前节点当成叶子节点，直接出错

需要特判五种情况

• 当前节点不存在
• 节点左孩子不存在
• 节点右孩子不存在
• 左右孩子都不存在
• 左右孩子都存在

class Solution {
   public:
    int minDepth(TreeNode* root) {
        if (!root)
            return 0;
        else if (!root->left && !root->right)
            return 1;
        else if (!root->left && root->right)
            return minDepth(root->right) + 1;
        else if (root->left && !root->right)
            return minDepth(root->left) + 1;
        else {
            int left = minDepth(root->left);
            int right = minDepth(root->right);
            return min(left, right) + 1;
        }
    }
};

O(n) 迭代 层序

当出队列的节点无左右孩子，立即返回当前层数

class Solution {
   public:
    int minDepth(TreeNode* root) {
        if (!root) return 0;
        int depth = 0;
        queue q;
        q.push(root);
        while (!q.empty()) {
            int n = q.size();
            depth++;
            for (int i = 0; i < n; i++) {
                auto t = q.front();
                q.pop();
                if (!t->left && !t->right) return depth;
                if (t->left) q.push(t->left);
                if (t->right) q.push(t->right);
            }
        }
        return depth;
    }
};

112 路径总和

112. 路径总和 - 力扣（LeetCode）

O(n) 递归

自顶向下，前序遍历

class Solution {
   public:
    bool hasPathSum(TreeNode* root, int targetSum) {
        if (!root) return false;
        targetSum -= root->val;
        if (!root->left && !root->right && targetSum == 0) return true;
        bool l1 = hasPathSum(root->left, targetSum);
        bool l2 = hasPathSum(root->right, targetSum);
        return l1 || l2;
    }
};

O(n) 迭代 前序

1. 初始化维护栈，将根节点及根节点的值入栈。
2. 当栈不为空时，弹出栈顶的节点及节点的值：

• • 若当前节点为叶子节点且累积值 val 为 targetSum，返回 true
  • 若当前节点的右子树不为空，将右孩子及 “val + 右孩子的值”入栈
  • 若当前节点的左子树不为空，将左孩子及”val + 左孩子的值“入栈

class Solution {
   public:
    bool hasPathSum(TreeNode* root, int targetSum) {
        if (!root) return false;
        stack> stk;
        stk.push({root, root->val});
        while (!stk.empty()) {
            auto t = stk.top();
            stk.pop();
            auto left = t.first->left;
            auto right = t.first->right;
            if (!left && !right && t.second == targetSum) return true;
            if (right) stk.push({right, t.second + right->val});
            if (left) stk.push({left, t.second + left->val});
        }
        return false;
    }
};

222 完全二叉树的节点个数

222. 完全二叉树的节点个数 - 力扣（LeetCode）

• 层序遍历算节点个数
• 递归 节点个数 = 左子树的节点个数 + 右子树的节点个数 + 1

O(n) 递归

class Solution {
   public:
    int countNodes(TreeNode* root) {
        if (!root) return 0;
        int left = countNodes(root->left);
        int right = countNodes(root->right);
        return left + right + 1;
    }
};

O(n) 层序

class Solution {
   public:
    int countNodes(TreeNode* root) {
        if (!root) return 0;
        int count = 0;
        queue q;
        q.push(root);
        while (!q.empty()) {
            int n = q.size();
            for (int i = 0; i < n; i++) {
                count++;
                auto t = q.front();
                q.pop();
                if (t->left) q.push(t->left);
                if (t->right) q.push(t->right);
            }
        }
        return count;
    }
};

O(logn)∗O(logn)

已知完全二叉树

• 左子树的深度等于右子树的深度的时候，左子树必定是满二叉树
• 左子树的深度大于右子树的深度的时候，右子树必定是满二叉树
• 满二叉树节点个数 2k−1

每次计算满二叉树的时候，计算的其实就是当前树高，即 O(logn)，每次递归调用的都是下一层的子树，总共调用了“树的高度”次，即 O(logn)，所以时间复杂度为 O(logn)∗O(logn)

class Solution {
   public:
    int height(TreeNode* root) {
        int height = 0;
        while (root) {
            root = root->left;  // 完全二叉树性质
            height++;
        }
        return height;
    }

    int countNodes(TreeNode* root) {
        if (!root) return 0;
        int left = height(root->left);
        int right = height(root->right);
        // 左子树深度 = 右子树深度，左子树为满二叉树
        if (left == right) return (1 << left) - 1 + 1 + countNodes(root->right);
        // 左子树深度 > 右子树深度，右子树为满二叉树
        // 节点数 = 左子树的深度 + 右子树的深度 + 根节点
        else
            return (1 << right) - 1 + 1 + countNodes(root->left);
    }
};

226 翻转二叉树

226. 翻转二叉树 - 力扣（LeetCode）

O(n) 递归 前序

class Solution {
   public:
    TreeNode* invertTree(TreeNode* root) {
        if (!root) return root;
        swap(root->left, root->right);
        invertTree(root->left);
        invertTree(root->right);
        return root;
    }
};

O(n) 迭代 前序

class Solution {
   public:
    TreeNode* invertTree(TreeNode* root) {
        if (!root) return root;
        stack stk;
        stk.push(root);
        while (!stk.empty()) {
            auto t = stk.top();
            stk.pop();
            swap(t->left, t->right);
            if (t->right) stk.push(t->right);
            if (t->left) stk.push(t->left);
        }
        return root;
    }
};

236 二叉树的最近公共祖先

236. 二叉树的最近公共祖先 - 力扣（LeetCode）

O(n) 递归 后序⭐

对于节点 p 和 q 来说，如果 node 为其最近公共祖先，那么 node 的左孩子和右孩子一定不是 p 和 q 的公共祖先

三种可能情况

• p 和 q 分别在节点 node 的左右子树中
• node 即为节点 p，q 在节点 p 的左子树或右子树中
• node 即为节点 q，p 在节点 q 的左子树或者右子树中

class Solution {
   public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if (!root) return nullptr;
        if (root == p || root == q) return root;
        TreeNode* left = lowestCommonAncestor(root->left, p, q);
        TreeNode* right = lowestCommonAncestor(root->right, p, q);
        if (left && right)
            return root;
        else if (!left && right)
            return right;
        else if (left && !right)
            return left;
        else if (!left && !right)
            return nullptr;
        else
            return nullptr;
    }
};

257 二叉树的所有路径

257. 二叉树的所有路径 - 力扣（LeetCode）

O(n) 递归 先序

class Solution {
   public:
    void preOrder(TreeNode* root, string path, vector<string>& ans) {
        if (!root) return;
        // 整形转字符串
        path += to_string(root->val);
        if (!root->left && !root->right)
            ans.push_back(path);
        else {
            path += "->";
            preOrder(root->left, path, ans);
            preOrder(root->right, path, ans);
        }
    }

    vector<string> binaryTreePaths(TreeNode* root) {
        vector<string> ans;
        preOrder(root, "", ans);
        return ans;
    }
};

O(n) 迭代 先序

• 初始化维护两个栈：一个栈是递归栈，将根节点入栈；另一个栈是路径栈，将根节点的值入栈（维护到当前节点的路径）

• 当栈不为空时，弹出两个栈的栈顶元素：

• • 若 node 为叶子节点，将路径加入结果集
  • 若 node 的右子树不为空，右孩子及右孩子的值分别入递归栈和路径栈
  • 若 node 的左子树不为空，左孩子及左孩子的值分别入递归栈和路径栈

class Solution {
   public:
    vector binaryTreePaths(TreeNode* root) {
        if (!root) return {};
        vector ans;
        stack s1;
        stack s2;
        s1.push(root);
        s2.push(to_string(root->val));
        while (!s1.empty()) {
            auto t = s1.top();
            s1.pop();
            auto path = s2.top();
            s2.pop();
            if (!t->left && !t->right) ans.push_back(path);
            if (t->right) {
                s1.push(t->right);
                s2.push(path + "->" + to_string(t->right->val));
            }
            if (t->left) {
                s1.push(t->left);
                s2.push(path + "->" + to_string(t->left->val));
            }
        }
        return ans;
    }
};

404 左叶子之和

404. 左叶子之和 - 力扣（LeetCode）

O(n) 递归 先序

左叶子节点就是“是左孩子且该左孩子没有孩子节点”

• 如果遍历的当前节点的左孩子是一个叶子节点，则左孩子的值累加入结果
• 如果遍历的当前节点的左孩子不是叶子节点，则继续遍历

class Solution {
   public:
    int ans = 0;
    void preOrder(TreeNode* root) {
        if (!root) return;
        if (root->left && !root->left->left && !root->left->right) {
            ans += root->left->val;
        }
        preOrder(root->left);
        preOrder(root->right);
    }

    int sumOfLeftLeaves(TreeNode* root) {
        ans = 0;
        if (!root) return ans;
        preOrder(root);
        return ans;
    }
};

513 找树左下角的值

513. 找树左下角的值 - 力扣（LeetCode）

O(n) 递归 先序

• 维护两个深度：最大深度 maxDepth、当前节点所处的深度 leftDepth
• 如果当前节点是叶子节点，且 leftDepth > maxDepth 的时候，更新 maxDepth 和当前的结果 ans
• 因为优先进行的是左子树的遍历，所以它肯定是当前层最左边的节点

class Solution {
   public:
    int ans, depthMax = -1;
    void preOrder(TreeNode* root, int depthNow) {
        if (!root) return;
        if (!root->left && !root->right && depthNow > depthMax) {
            depthMax = depthNow;
            ans = root->val;
        }
        preOrder(root->left, depthNow + 1);
        preOrder(root->right, depthNow + 1);
    }

    int findBottomLeftValue(TreeNode* root) {
        // if(!root) return -1; 至少有一个节点
        preOrder(root, 1);
        return ans;
    }
};

O(n) 迭代 层次

使用队列保存每一层的节点，第 1 个出队列的节点值保存(即该层最左边的值)，把队列里的所有节点出队列，然后把这些出去节点各自的子节点入队列。

class Solution {
   public:
    int findBottomLeftValue(TreeNode* root) {
        int ans;
        queue q;
        q.push(root);
        while (!q.empty()) {
            int n = q.size();
            for (int i = 0; i < n; i++) {
                auto t = q.front();
                q.pop();
                if (i == 0) ans = t->val;
                if (t->left) q.push(t->left);
                if (t->right) q.push(t->right);
            }
        }
        return ans;
    }
};

559 N叉树的最大深度

559. N 叉树的最大深度 - 力扣（LeetCode）

O(n) 递归 自底向上

class Solution {
   public:
    int maxDepth(Node* root) {
        if (!root) return 0;
        int ans = 0;
        for (auto c : root->children) {
            ans = max(maxDepth(c), ans);
        }
        return ans + 1;
    }
};

O(n) 迭代 层序

class Solution {
   public:
    int maxDepth(Node* root) {
        if (!root) return 0;
        queue q;
        q.push(root);
        int depth = 0;
        while (!q.empty()) {
            depth++;
            int n = q.size();
            for (int i = 0; i < n; i++) {
                auto t = q.front();
                q.pop();
                for (auto c : t->children) {
                    q.push(c);
                }
            }
        }
        return depth;
    }
};

617 合并二叉树

617. 合并二叉树 - 力扣（LeetCode）

O(n) 递归 前序

• 如果两棵树对应位置上都有节点，则新节点的值为两个节点的值相加
• 如果两棵树对应位置上只有一个节点有值，则新节点的值就为该节点的值

class Solution {
   public:
    TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
        if (!root1)
            return root2;
        else if (!root2)
            return root1;
        TreeNode* node = new TreeNode(root1->val + root2->val);
        node->left = mergeTrees(root1->left, root2->left);
        node->right = mergeTrees(root1->right, root2->right);
        return node;
    }
};

O(n) 迭代 层序 思路 🍔

ACM 选手图解 LeetCode 合并二叉树 (qq.com)

• 维护两个队列，队列 queueMerge 存储合并后的树节点，queue 则是 root1 和 root2 的节点
• 初始化：创建一个新的根节点 root，其值为 root1.val + root2.val，同时初始化两个队列，将 root 入 queueMerge 队列，将 root1 和 root2 入 queue 队列

654 最大二叉树

654. 最大二叉树 - 力扣（LeetCode）

O(n) 递归 前序 分治

• 划分：每次找到区间里的最大值，最大值左边为左子树，右边为右子树

class Solution {
   public:
    TreeNode* dfs(vector<int>& nums, int start, int end) {
        if (start > end) return nullptr;
        int maxIndex = start;
        for (int i = start; i <= end; i++)
            if (nums[i] > nums[maxIndex]) maxIndex = i;
        auto node = new TreeNode(nums[maxIndex]);
        node->left = dfs(nums, start, maxIndex - 1);
        node->right = dfs(nums, maxIndex + 1, end);
        return node;
    }
    TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
        return dfs(nums, 0, nums.size() - 1);
    }
};

参考资料

算法小白的 LeetCode 刷题顺序

什么是最好、最坏、平均、均摊时间复杂度? - 知乎 (zhihu.com)

• 时间、空间复杂度
•     事后统计法
•         缺点
•     时间、空间复杂度
•         时间复杂度
•         对数换底公式
•         最好、最坏、平均情况
•         均摊时间复杂度
•         空间复杂度
• 数组
•     27 移除元素
•         O(n2) 朴素
•         O(n) 双指针
•     59 螺旋矩阵 II
•         O(n2) 状态移动
•     209 长度最小子数组
•         O(n2) 滑动窗口
•     977 有序数组的平方
•         O(n) 双指针
• 单链表
•     19 删除倒数第 N 节点
•         O(n) 双指针
•     24 两两交换
•         O(n) 三指针
•     25 K 个一组翻转
•         O(n) 翻转子链表
•     141 环形链表
•         O(n) 快慢指针
•     142 环形链表 II
•         O(n) 数学思想
•     160 相交链表
•         O(n+m) 数学思想
•     206 翻转链表
•         O(n) 头插法
•     707 设计链表
•         考查代码功底
• 栈
•     20 有效括号
•         O(n) 栈 朴素
•         O(n) 栈 STL
•     150 逆波兰表达式
•         O(n) 栈 STL
•     232 用栈实现队列
•         O(1) 两栈 STL
•     1047 删除字符串中的所有相邻重复项
•         O(n) 栈 字符串
• 队列
•     225 用队列实现栈
•         O(n) 两队列 STL
•         O(n) 单队列 STL
•     239 滑动窗口最大值
•         O(n) 单调队列 STL
• 字符串
•     JZ05 替换空格
•     JZ58 左旋转字符串
•     151 反转字符串中的单词
•         从后往前、双指针
•         分解问题、双指针
•     344 反转字符串
•         O(n) 双指针
•     541 反转字符串 II
•         O(n) 双指针
• 哈希表
•     1 两数之和
•         O(n) 哈希表 STL
•     15 三数之和
•         O(n2) 双指针
•         O(n2) 哈希表 超时
•     202 快乐数
•         O(logn) 哈希表 STL
•     242 有效的字母异位词
•         O(n+m) 哈希表 STL
•     349 两个数组的交集
•         O(n+m) 哈希表 STL
•     383 赎金信
•         O(n+m) 哈希表 数组
•     454 四数相加Ⅱ
•         O(n2) 哈希表 STL
•     575 分糖果
•         O(n) 哈希表 STL
• 递归
• 迭代
• 分治
• 二叉树
•     144 前序遍历
•         O(n) 递归
•         O(n) 迭代
•     94 中序遍历
•         O(n) 递归
•         O(n) 迭代 ⭐
•     145 后序遍历
•         O(n) 递归
•         O(n) 迭代 ⭐
•     102 层序遍历
•         O(n) 迭代 队列
•     100 相同的树
•         O(min(n,m)) 递归
•         O(n) 迭代 层序
•     101 对称二叉树
•         O(n) 递归
•         O(n) 迭代 层序
•     104 二叉树的最大深度
•         O(n) 递归
•         O(n) 迭代 层序
•     111 二叉树最小深度 ⭐
•         O(n) 递归
•         O(n) 迭代 层序
•     112 路径总和
•         O(n) 递归
•         O(n) 迭代 前序
•     222 完全二叉树的节点个数
•         O(n) 递归
•         O(n) 层序
•         O(logn)∗O(logn)
•     226 翻转二叉树
•         O(n) 递归 前序
•         O(n) 迭代 前序
•     236 二叉树的最近公共祖先
•         O(n) 递归 后序⭐
•     257 二叉树的所有路径
•         O(n) 递归 先序
•         O(n) 迭代 先序
•     404 左叶子之和
•         O(n) 递归 先序
•     513 找树左下角的值
•         O(n) 递归 先序
•         O(n) 迭代 层次
•     559 N叉树的最大深度
•         O(n) 递归 自底向上
•         O(n) 迭代 层序
•     617 合并二叉树
•         O(n) 递归 前序
•         O(n) 迭代 层序 思路 🍔
•     654 最大二叉树
•         O(n) 递归 前序 分治
• 参考资料

__EOF__